8.4.1 单项式与单项式相乘 同步练习
文档属性
| 名称 | 8.4.1 单项式与单项式相乘 同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 371.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-22 20:56:49 | ||
图片预览
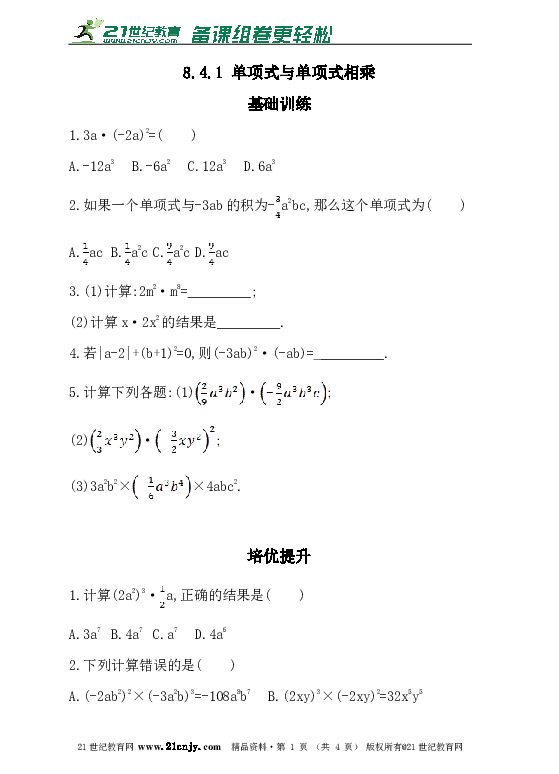


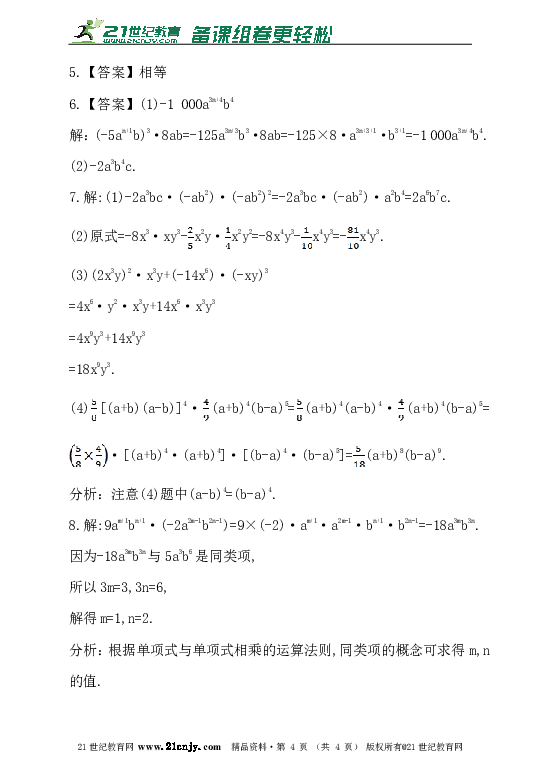
文档简介
8.4.1 单项式与单项式相乘
基础训练
1.3a·(-2a)2=( )
A.-12a3 B.-6a2 C.12a3 D.6a3
2.如果一个单项式与-3ab的积为-a2bc,那么这个单项式为( )
A.ac B.a2c C.a2c D.ac
3.(1)计算:2m2·m8=_________;
(2)计算x·2x2的结果是_________.
4.若|a-2|+(b+1)2=0,则(-3ab)2·(-ab)= _________.
5.计算下列各题:(1)·;
(2)·;
(3)3a2b2××4abc2.
培优提升
1.计算(2a2)3·a,正确的结果是( )
A.3a7 B.4a7 C.a7 D.4a6
2.下列计算错误的是( )
A.(-2ab2)2×(-3a2b)3=-108a8b7 B.(2xy)3×(-2xy)2=32x5y5
C.×x2y=x4y3 D.m2n×=m4n4
3.计算(-6xny)2·3xn-1y的结果是( )
A.18x3n-1y2 B.-36x2n-1y3 C.-108x3n-1y2 D.108x3n-1y3
4.计算:3a2b3·2a2b=___________.
5.若m为正偶数,则(a-b)m·(b-a)n与(b-a)m+n的结果__________.(填“相等”或“互为相反数”)?21教育网
6.计算 :(1)(-5an+1b)3·8ab=__________;
(2)3ab··2abc=__________.
7.计算:
(1)-2a3bc·(-ab2)·(-ab2)2;
(2)(-2x)3·xy3-x2y·;
(3)(2x3y)2·x3y+(-14x6)·(-xy)3;
(4)[(a+b)(a-b)]4·(a+b)4(b-a)5.
8.已知单项式9am+1bn+1与-2a2m-1b2n-1的积与5a3b6是同类项,求m,n的值.
9.有理数x,y满足+=0,求
(-2xy)2·(-y2)·6xy2的值.
10.光的速度约是3×105千米/秒,有一颗恒星发射的光要10年才能到达地球,若一年以3.1×107秒计算,这颗恒星距离地球有多少千米?
参考答案
【基础训练】
1.【答案】C 2.【答案】A
3.【答案】(1)2m10 (2)2x3
4.【答案】72
5.解:(1)原式=×·a3+3·b2+3·c=-a6b5c.
(2)原式=x3y2·x2y4=x5y6.
(3)3a2b2××4abc2=×(a2×a3×a)×(b2×b4×b)×c2=-2a6b7c2.21世纪教育网版权所有
【培优提升】
1.【答案】B
2.【答案】D
解:m2n×=m2n×m2n4=·m2+2·n1+4=m4n5.
3.【答案】D
4.【答案】6a4b4
5.【答案】相等
6.【答案】(1)-1 000a3n+4b4
解:(-5an+1b)3·8ab=-125a3n+3b3·8ab=-125×8·a3n+3+1·b3+1=-1 000a3n+4b4.
(2)-2a3b4c.
7.解:(1)-2a3bc·(-ab2)·(-ab2)2=-2a3bc·(-ab2)·a2b4=2a6b7c.
(2)原式=-8x3·xy3-x2y·x2y2=-8x4y3-x4y3=-x4y3.
(3)(2x3y)2·x3y+(-14x6)·(-xy)3
=4x6·y2·x3y+14x6·x3y3
=4x9y3+14x9y3
=18x9y3.
(4)[(a+b)(a-b)]4·(a+b)4(b-a)5=(a+b)4(a-b)4·(a+b)4(b-a)5=·[(a+b)4·(a+b)4]·[(b-a)4·(b-a)5]=(a+b)8(b-a)9.
分析:注意(4)题中(a-b)4=(b-a)4.
8.解:9am+1bn+1·(-2a2m-1b2n-1)=9×(-2)·am+1·a2m-1·bn+1·b2n-1=-18a3mb3n.
因为-18a3mb3n与5a3b6是同类项,
所以3m=3,3n=6,
解得m=1,n=2.
分析:根据单项式与单项式相乘的运算法则,同类项的概念可求得m,n的值.
9.解:因为+x+3y+2=0,
所以解得
所以
(-2xy)2·(-y2)·6xy2=4x2y2·(-y2)·6xy2=-24x3y6=-24×(-4)3×=-24×(-22)3×=24×26×=24×=24×1=24.
10.解:3×105×3.1×107×10=9.3×1013(千米).
分析:这颗恒星距离地球有9.3×1013 千米.
基础训练
1.3a·(-2a)2=( )
A.-12a3 B.-6a2 C.12a3 D.6a3
2.如果一个单项式与-3ab的积为-a2bc,那么这个单项式为( )
A.ac B.a2c C.a2c D.ac
3.(1)计算:2m2·m8=_________;
(2)计算x·2x2的结果是_________.
4.若|a-2|+(b+1)2=0,则(-3ab)2·(-ab)= _________.
5.计算下列各题:(1)·;
(2)·;
(3)3a2b2××4abc2.
培优提升
1.计算(2a2)3·a,正确的结果是( )
A.3a7 B.4a7 C.a7 D.4a6
2.下列计算错误的是( )
A.(-2ab2)2×(-3a2b)3=-108a8b7 B.(2xy)3×(-2xy)2=32x5y5
C.×x2y=x4y3 D.m2n×=m4n4
3.计算(-6xny)2·3xn-1y的结果是( )
A.18x3n-1y2 B.-36x2n-1y3 C.-108x3n-1y2 D.108x3n-1y3
4.计算:3a2b3·2a2b=___________.
5.若m为正偶数,则(a-b)m·(b-a)n与(b-a)m+n的结果__________.(填“相等”或“互为相反数”)?21教育网
6.计算 :(1)(-5an+1b)3·8ab=__________;
(2)3ab··2abc=__________.
7.计算:
(1)-2a3bc·(-ab2)·(-ab2)2;
(2)(-2x)3·xy3-x2y·;
(3)(2x3y)2·x3y+(-14x6)·(-xy)3;
(4)[(a+b)(a-b)]4·(a+b)4(b-a)5.
8.已知单项式9am+1bn+1与-2a2m-1b2n-1的积与5a3b6是同类项,求m,n的值.
9.有理数x,y满足+=0,求
(-2xy)2·(-y2)·6xy2的值.
10.光的速度约是3×105千米/秒,有一颗恒星发射的光要10年才能到达地球,若一年以3.1×107秒计算,这颗恒星距离地球有多少千米?
参考答案
【基础训练】
1.【答案】C 2.【答案】A
3.【答案】(1)2m10 (2)2x3
4.【答案】72
5.解:(1)原式=×·a3+3·b2+3·c=-a6b5c.
(2)原式=x3y2·x2y4=x5y6.
(3)3a2b2××4abc2=×(a2×a3×a)×(b2×b4×b)×c2=-2a6b7c2.21世纪教育网版权所有
【培优提升】
1.【答案】B
2.【答案】D
解:m2n×=m2n×m2n4=·m2+2·n1+4=m4n5.
3.【答案】D
4.【答案】6a4b4
5.【答案】相等
6.【答案】(1)-1 000a3n+4b4
解:(-5an+1b)3·8ab=-125a3n+3b3·8ab=-125×8·a3n+3+1·b3+1=-1 000a3n+4b4.
(2)-2a3b4c.
7.解:(1)-2a3bc·(-ab2)·(-ab2)2=-2a3bc·(-ab2)·a2b4=2a6b7c.
(2)原式=-8x3·xy3-x2y·x2y2=-8x4y3-x4y3=-x4y3.
(3)(2x3y)2·x3y+(-14x6)·(-xy)3
=4x6·y2·x3y+14x6·x3y3
=4x9y3+14x9y3
=18x9y3.
(4)[(a+b)(a-b)]4·(a+b)4(b-a)5=(a+b)4(a-b)4·(a+b)4(b-a)5=·[(a+b)4·(a+b)4]·[(b-a)4·(b-a)5]=(a+b)8(b-a)9.
分析:注意(4)题中(a-b)4=(b-a)4.
8.解:9am+1bn+1·(-2a2m-1b2n-1)=9×(-2)·am+1·a2m-1·bn+1·b2n-1=-18a3mb3n.
因为-18a3mb3n与5a3b6是同类项,
所以3m=3,3n=6,
解得m=1,n=2.
分析:根据单项式与单项式相乘的运算法则,同类项的概念可求得m,n的值.
9.解:因为+x+3y+2=0,
所以解得
所以
(-2xy)2·(-y2)·6xy2=4x2y2·(-y2)·6xy2=-24x3y6=-24×(-4)3×=-24×(-22)3×=24×26×=24×=24×1=24.
10.解:3×105×3.1×107×10=9.3×1013(千米).
分析:这颗恒星距离地球有9.3×1013 千米.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
