第七章 相交线与平行线 单元测试卷

第七章 相交线与平行线 单元测试卷
一、选择题(每题3分,共30分)
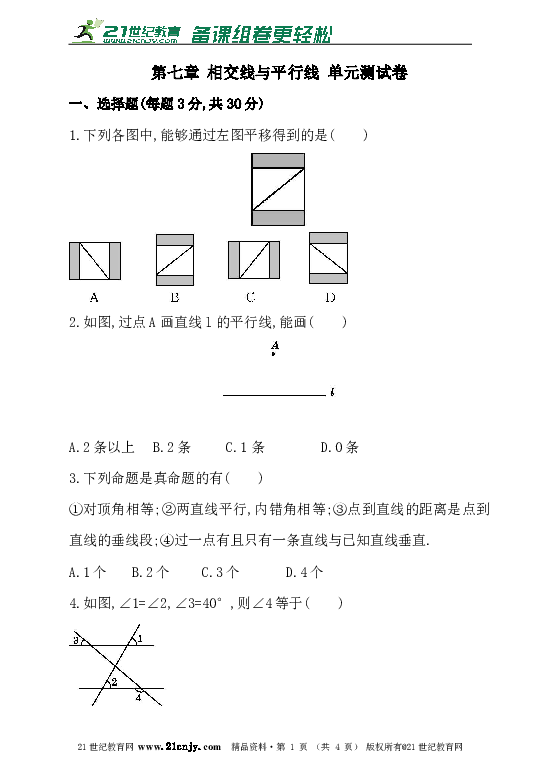
1.下列各图中,能够通过左图平移得到的是(　　)
2.如图,过点A画直线l的平行线,能画(　　)
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
A.2条以上 B.2条 C.1条 D.0条
3.下列命题是真命题的有(　　)
①对顶角相等;②两直线平行,内错角相等;③点到直线的距离是点到直线的垂线段;④过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
4.如图,∠1=∠2,∠3=40°,则∠4等于(　　)
A.120° B.130° C.140° D.40°
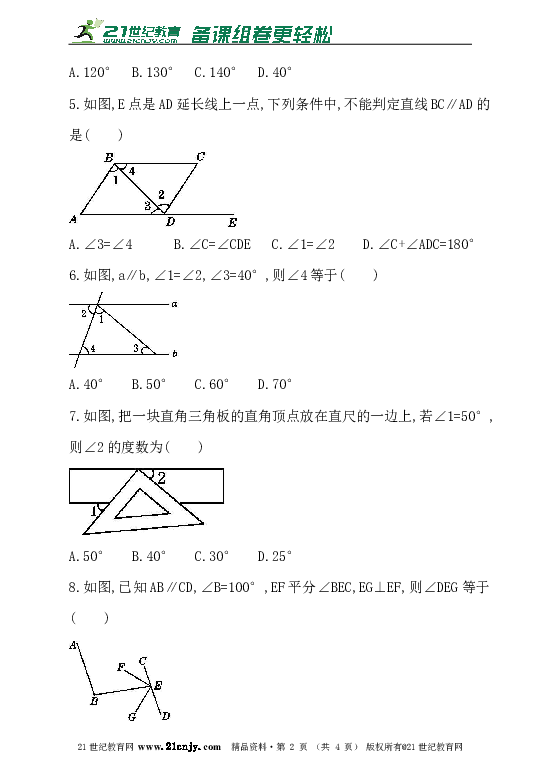
5.如图,E点是AD延长线上一点,下列条件中,不能判定直线BC∥AD的是(　　)
A.∠3=∠4 B.∠C=∠CDE C.∠1=∠2 D.∠C+∠ADC=180°
6.如图,a∥b,∠1=∠2,∠3=40°,则∠4等于(　　)
A.40° B.50° C.60° D.70°
7.如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为(　　)
A.50° B.40° C.30° D.25°
8.如图,已知AB∥CD,∠B=100°,EF平分∠BEC,EG⊥EF,则∠DEG等于(　　)
A.50° B.40° C.60° D.70°
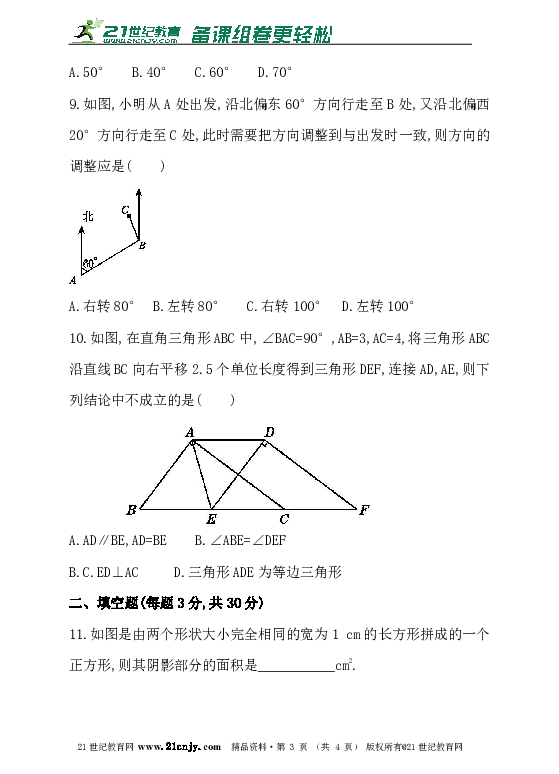
9.如图,小明从A处出发,沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需要把方向调整到与出发时一致,则方向的调整应是(　　)21·cn·jy·com
A.右转80° B.左转80° C.右转100° D.左转100°
10.如图,在直角三角形ABC中,∠BAC=90°,AB=3,AC=4,将三角形ABC沿直线BC向右平移2.5个单位长度得到三角形DEF,连接AD,AE,则下列结论中不成立的是(　　)21·世纪*教育网
AD∥BE,AD=BE B.∠ABE=∠DEF
C.ED⊥AC D.三角形ADE为等边三角形
二、填空题(每题3分,共30分)
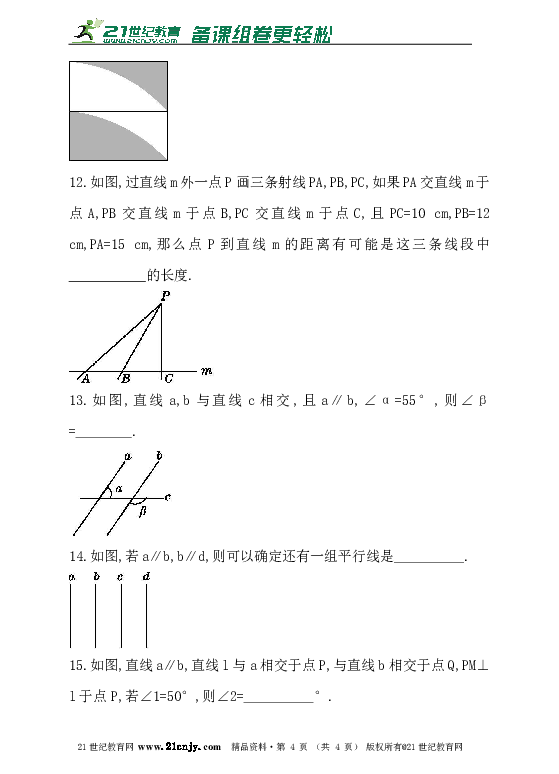
11.如图是由两个形状大小完全相同的宽为1 cm的长方形拼成的一个正方形,则其阴影部分的面积是___________cm2.www.21-cn-jy.com
12.如图,过直线m外一点P画三条射线PA,PB,PC,如果PA交直线m于点A,PB交直线m于点B,PC交直线m于点C,且PC=10 cm,PB=12 cm,PA=15 cm,那么点P到直线m的距离有可能是这三条线段中___________的长度.21世纪教育网版权所有
13.如图,直线a,b与直线c相交,且a∥b,∠α=55°,则∠β=　　　　.
14.如图,若a∥b,b∥d,则可以确定还有一组平行线是　　　　　.
15.如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2=　　　　　°.www-2-1-cnjy-com
16.命题“如果a=b,那么=”的条件是___________,这是个___________命题(填“真”或“假”).?2-1-c-n-j-y
17.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=___________.
18.将一副直角三角尺按如图所示的方式放置,若AE∥BC,则∠CAD=　　　　　.
19.如图是由五个同样的三角形组成的图案,三角形的三个内角的度数分别为36°,72°,72°,则图中共有　　　　　对平行线.
20.图中有_________对同位角,有_________对内错角,有_________对同旁内角.【来源：21·世纪·教育·网】
三、解答题(21、22题每题6分,23、24题每题8分,25题12分,共40分)
21.如图,已知公路l和公路边上一个加油站A以及工厂B.
(1)画出从工厂B到加油站A的最短路线,并说明理由;
(2)画出从工厂B到公路l的最短路线,并说明理由.
22.如图,AB∥CD,OE平分∠AOC,OE⊥OF,点O为垂足,∠C=50°,求∠AOF的度数.
23.如图,已知∠A=∠F,∠C=∠D,试说明:∠1=∠2.
24.三角形ABC和三角形DEF是两个形状、大小完全相同的直角三角形,如图(1)所示,三条边BC,AB,AC的长分别是6 cm,8 cm,10 cm,且B,C,D,F在同一条直线上.【来源：21cnj*y.co*m】
(1)若三角形ABC朝着某个方向平移后得如图(2)所示的图形,则三角形ABC平移的方向是什么?平移的距离是多少?【版权所有：21教育】
(2)三角形ABC平移至图(3)所示的位置,若BD=6.4 cm,则三角形EBF的面积是多少?
25.(1)如图(1),已知AB∥DF,则∠BCF,∠B,∠F之间有怎样的数量关系?并说明理由;
(2)让点C向左移动,如图(2),则∠BCF,∠B,∠F之间有怎样的数量关系?并说明理由;
(3)让点C移动到直线AB的上方,如图(3),则∠BCF,∠B,∠F之间有怎样的数量关系?
参考答案
一、1.【答案】B　
解：平移不改变图形的形状、大小和朝向.A图形需要旋转才能得到,C图形需要旋转再翻折才能得到,D图形需要翻折才能得到,故A、C、D都不能由题中左图通过平移得到,只有B除位置不同外,其他与题中左图完全相同.21*cnjy*com
2.【答案】C
3.【答案】B　
解：①是对顶角的性质,正确;②是平行线的性质,正确;点到直线的距离是数量,而点到直线的垂线段是图形,二者不同,③错误;④少条件“在同一平面内”,故④错.综上可知,正确的命题有2个.
4.【答案】C
5.【答案】C　
解：∠3与∠4是由BC和AD被BD所截构成的内错角,若∠3=∠4,则一定有BC∥AD;∠C与∠CDE是由BC和AE被CD所截构成的内错角,若∠C=∠CDE,则一定有BC∥AD;∠1与∠2虽然是内错角,但它们不是由BC,AD与它们的截线构成的,即使相等,也不能判定BC∥AD;∠C与∠ADC是由BC,AD被CD所截构成的同旁内角,若∠C+∠ADC=180°,则有BC∥AD.21cnjy.com
6.【答案】D　7.【答案】B
8.【答案】A　
解：由AB∥CD,∠B=100°,得∠BED=100°,∴∠
BEC=180°-100°=80°.又EF平分∠BEC,∴∠BEF=40°.由EG⊥EF,得∠GEF=90°,∴∠BEG=90°-40°=50°.∴∠DEG=100°-50°=50°.
9.【答案】A　
解：如图,出发时是AD方向,到达C点时是BF方向,把方向调整到与出发时一致,就是在C点沿CF方向右转∠FCE,变为CE方向.
因为CE∥AD,所以∠FCE=∠FBD=∠1+∠2.由题意,知∠1=20°,∠2=60°,所以∠FCE=80°,即右转80°可调整到与出发时一致的方向.
10.【答案】D　
解：由“连接各组对应点的线段平行(或在同一条直线上)且相等”,知AD∥BE,AD=BE,故A正确;由“平移前后的图形对应角相等”,知∠ABE=∠DEF,故B正确;因为DE是由AB平移得到的,所以DE∥AB,由平行线的性质易知ED⊥AC,故C正确;由题意,AD=2.5,DE=AB=3,所以三角形ADE不是等边三角形,故D错.21教育名师原创作品
二、11.【答案】2　
解：如图,容易看出,通过平移,1,2两部分可以重合,3,4两部分也可以重合,所以阴影部分的面积是正方形面积的一半,即等于2 cm2.
12.【答案】PC　13.【答案】125°
14.【答案】a∥d　
解：因为a,d都和b平行,所以a∥d.
15.【答案】40
16.【答案】a=b;假　
解：在用“如果……那么……”表示的命题中,“如果”后面的部分是条件,“那么”后面的部分是结论.由于本题条件没有强调c≠0,故结论不成立,是假命题.21*cnjy*com
17.【答案】140°
18.【答案】15°　
解：一副直角三角尺的内角度数分别为30°,60°,90°与45°,45°,90°,这是一个隐含条件.利用这个条件及平行线的性质,即可求出∠CAD.
19.【答案】5　
20.【答案】0;4;0　
解：观察题图可知,没有同位角和同旁内角,内错角有4对,分别是:∠ABC与∠DCB,∠ECB与∠FBC,∠DCB与∠CBF,∠ABC与∠ECB.
三、21.解:(1)如图,连接AB,则线段AB为从工厂B到加油站A的最短路线.理由:两点之间,线段最短.【出处：21教育名师】
(第21(1)题)
(第21(2)题)
(2)如图,过点B向直线l作垂线,垂足为点C,则从工厂B到公路l的最短路线为线段BC.理由:连接直线外一点与直线上各点的所有线段中,垂线段最短.
22.解:∵AB∥CD,∴∠AOC=∠C.又∵∠C=50°,
∴∠AOC=50°.∵OE平分∠AOC,∴∠AOE=∠AOC=×50°=25°.∵OE⊥OF,∴∠EOF=90°.∴∠AOF=∠AOE+∠EOF=25°+90°=115°.
分析：本题主要考查垂直的定义、角平分线的定义和平行线的性质.
23.解:∵∠A=∠F,∴DF∥AC(内错角相等,两直线平行).
∴∠D+∠DBC=180°(两直线平行,同旁内角互补).
∵∠D=∠C,∴∠C+∠DBC=180°.
∴DB∥CE(同旁内角互补,两直线平行.)
∴∠1=∠ANC(两直线平行,同位角相等).
∵∠ANC=∠2,∴∠1=∠2(等量代换).
24.解:(1)由题图可知,三角形ABC平移的方向是BC方向,∵BC=6 cm,∴平移距离是6 cm.
(2)∵BD=6.4 cm,DF=AC=10 cm,
∴BF=DF-BD=10-6.4=3.6(cm).
设BE=x cm,根据题意,得×10x=×6×8.解得x=4.8.∴三角形EBF的面积是BE·BF=×4.8×3.6=8.64(cm2).
分析：本题考查平移的概念与性质,三角形面积的计算方法.注意“用两种方法计算同一个三角形的面积”是一种重要的方法,应用较广,它也是一种等量关系,用此关系可以求某条线段的长.
25.解:(1)∠B+∠BCF+∠F=360°.理由如下:如图(1),过点C在∠BCF内部作CE∥AB.
∵AB∥DF,
∴AB∥CE∥DF.
∴∠B+∠BCE=180°,∠F+∠ECF=180°.
∴∠B+∠BCE+∠F+∠ECF=360°,即∠B+∠BCF+∠F=360°.
(2)∠BCF=∠B+∠F.理由如下:如图(2),过点C在∠BCF内部作CE∥AB.
∵AB∥DF,∴AB∥CE∥DF.∴∠B=∠BCE,∠F=∠ECF.∴∠B+∠F=∠BCE+∠ECF,即∠BCF=∠B+∠F.2·1·c·n·j·y
(3)如图(3),过点C作CE∥AB.
∵AB∥DF,∴AB∥CE∥DF.∴∠F=∠ECF,∠B=∠BCE.∵∠BCF=∠ECF-∠BCE,21教育网
∴∠BCF=∠F-∠B.