第八章 整式的乘法 单元测试卷

第八章 整式的乘法 单元测试卷
一、选择题(每题3分,共30分)
1.计算(4x2y3)3的结果是(　　)
A.4x6y9 B.4x5y6 C.64x6y9 D.64x5y6
2.计算a·a-1的结果为(　　)
A.-1 B.0 C.1 D.-a
3.下列运算中,结果是a5的是(　　)
A.a2·a3 B.a10÷a2 C.(a2)3 D.(-a)5
4.下列计算正确的是(　　)
A.x2·x3=x6 B.(x3)2=x5 C.(xy2)3=x3y6 D.x6÷x3=x2
5.化简代数式(x+y)2(x-y)2为(　　)
A.x4-y4 B.x4-2x2y2+y4 C.x2-2xy+y2 D.x4+y4
6.世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000 000 076克.将0.000 000 076用科学记数法表示为(　　)21cnjy.com
A.7.6×10-8 B.0.76×10-9 C.7.6×105 D.0.76×109
7.如果(2x+m)(x-5)的化简结果中不含x的一次项,那么m等于(　　)
A.-10 B.1 C.10 D.2
8.如果单项式-xa+1y3与ybx2是同类项,那么a,b的值分别为(　　)
A.a=2,b=3 B.a=1,b=2 C.a=1,b=3 D.a=2,b=2
9.若(-a2)·(-a)2·(-a)m>0,则(　　)
A.m为奇数 B.m为偶数 C.a>0,m为奇数 D.a>0,m为偶数
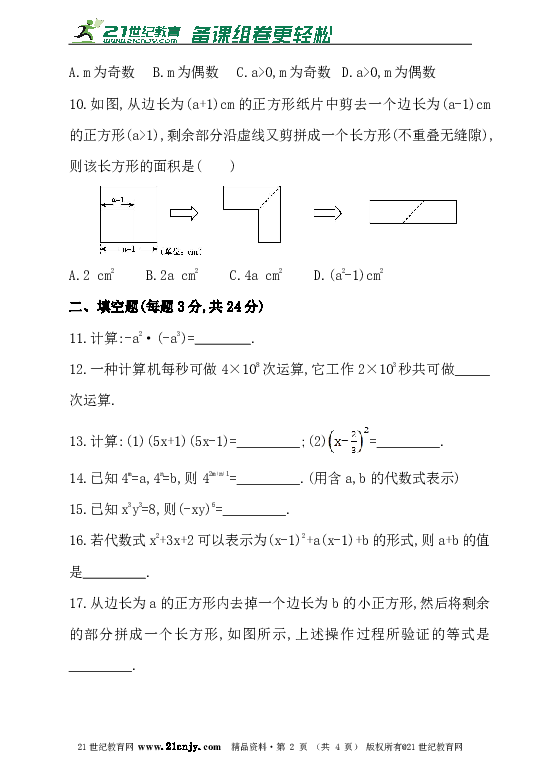
10.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则该长方形的面积是(　　)【来源：21·世纪·教育·网】
A.2 cm2 B.2a cm2 C.4a cm2 D.(a2-1)cm2
二、填空题(每题3分,共24分)
11.计算:-a2·(-a3)=________.
12.一种计算机每秒可做4×108次运算,它工作2×103秒共可做_____次运算.
13.计算:(1)(5x+1)(5x-1)=_________;(2)=_________.?
14.已知4m=a,4n=b,则42m+n+1=_________.(用含a,b的代数式表示)?
15.已知x3y3=8,则(-xy)6=_________.
16.若代数式x2+3x+2可以表示为(x-1)2+a(x-1)+b的形式,则a+b的值是_________.2·1·c·n·j·y
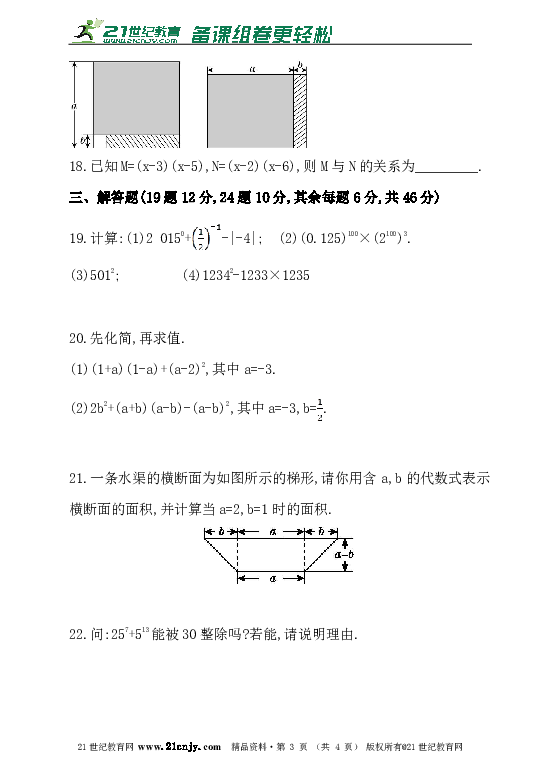
17.从边长为a的正方形内去掉一个边长为b的小正方形,然后将剩余的部分拼成一个长方形,如图所示,上述操作过程所验证的等式是_________.21·世纪*教育网
18.已知M=(x-3)(x-5),N=(x-2)(x-6),则M与N的关系为_________.
三、解答题(19题12分,24题10分,其余每题6分,共46分)
19.计算:(1)2 0150+-|-4|;　(2)(0.125)100×(2100)3.
(3)5012; (4)12342-1233×1235
20.先化简,再求值.
(1)(1+a)(1-a)+(a-2)2,其中a=-3.
(2)2b2+(a+b)(a-b)-(a-b)2,其中a=-3,b=.
21.一条水渠的横断面为如图所示的梯形,请你用含a,b的代数式表示横断面的面积,并计算当a=2,b=1时的面积.2-1-c-n-j-y
22.问:257+513能被30整除吗?若能,请说明理由.
23.若x3(3xn-2xm+4xk)=3x5-2x6+4x4,求-3k2(n3mk+2km2)的值.
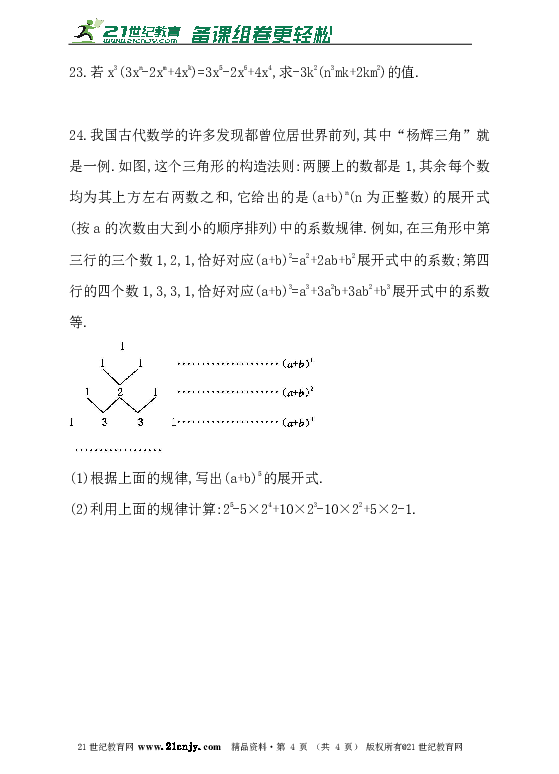
24.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出的是(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)中的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等.21·cn·jy·com
(1)根据上面的规律,写出(a+b)5的展开式.
(2)利用上面的规律计算:25-5×24+10×23-10×22+5×2-1.
参考答案
一、1.【答案】C　2.【答案】C　3.【答案】A　
4.【答案】C
5.【答案】B　
解：(x+y)2(x-y)2=[(x+y)(x-y)]2=(x2-y2)2=x4-2x2y2+y4.
6.【答案】A　7.【答案】C　8.【答案】C　9.【答案】C
10.【答案】C　
解：本题运用数形结合思想.根据题意得出长方形的面积是[(a+1)2-(a-1)2]cm2.
二、11.【答案】a5　12.【答案】8×1011
13.【答案】(1)25x2-1　(2)x2-x+
14.【答案】4a2b　
解：本题运用整体思想.42m+n+1=42m·4n·4=(4m)2·4n·4=4a2b.
15.【答案】64　
解：(-xy)6=x6y6=(x3y3)2=82=64.
16.【答案】11　
解：本题运用方程思想.(x-1)2+a(x-1)+b=x2+(a-2)x+1-a+b.这个代数式与x2+3x+2相等,因此对应的系数相等,即a-2=3,1-a+b=2,所以a=5,b=6,所以a+b=11.21世纪教育网版权所有
17.【答案】a2-b2=(a+b)(a-b)
18.【答案】M>N　
解：M=x2-8x+15,N=x2-8x+12.
三、19.解:(1)2 0150+-|-4|=1+2-4=-1.
(2)(0.125)100×(2100)3=(0.125)100×(23)100=(0.125×8)100=1100=1.
(3)5012=(500+1)2=5002+2×500×1+12
=250000+1000+1
=251001.
(4)12342-1233×1235
=12342-(1234-1)×(1234+1)
=12342-12342+1
=1.
20.解:(1)(1+a)(1-a)+(a-2)2
=1-a2+a2-4a+4
=5-4a
当a=-3时,原式=5-4×(-3)=17.
(2)2b2+(a+b)(a-b)-(a-b)2
=2b2+a2-b2-(a2-2ab+b2)
=a2+b2-a2+2ab-b2
=2ab
当a=-3,b=时,原式=2×(-3)×=-3.
21.解:水渠的横断面的面积:
　[(b+a+b)+a]·(a-b)
=(2a+2b)(a-b)
=(a+b)(a-b)
=a2-b2
当a=2,b=1时,水渠的横断面的面积为:a2-b2=22-12=4-1=3.
22.解:能.理由如下:
257+513=(52)7+513=514+513=5×513+513=513(5+1)=6×513=30×512.
因为512是个整数,所以257+513能被30整除.
分析：把257+513表示为30与一个整数乘积的形式是解本题的关键.
23.解:x3(3xn-2xm+4xk)=3x3+n-2x3+m+4x3+k=3x5-2x6+4x4www.21-cn-jy.com
∴3+n=5,3+m=6,3+k=4.
∴n=2,m=3,k=1.
∴-3k2(n3mk+2km2)
=-3k3n3m-6k3m2
=-3×1×23×3-6×1×32
=-72-54
=-126.
24.解:(1)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
(2)原式
=25+5×24×(-1)+10×23×(-1)2+10×22×(-1)3+5×2×(-1)4+(-1)5=(2-1)5=1.21教育网