第九章 三角形 单元测试卷

第九章 三角形 单元测试卷
一、选择题(每题3分,共30分)
1.下列命题中,是真命题的是(　　)
A.三角形的角平分线与角的平分线都是射线
B.三角形的角平分线与角的平分线都是线段
C.三角形的角平分线是射线,角的平分线是线段
D.三角形的角平分线是线段,角的平分线是射线
2.下列各组数可能是一个三角形的边长的是(　　)
A.1,2,4 B.4,5,9 C.4,6,8 D.5,5,11
3.一个三角形的两个内角分别是55°和65°,下列度数的角不可能是这个三角形的外角的是(　　)
A.130° B.125° C.120° D.115°
4.下列说法中,错误的是(　　)
A.一个三角形中至少有一个角不小于60°
B.直角三角形只有一条高
C.三角形的中线不可能在三角形外部
D.三角形的一条中线把三角形分成面积相等的两部分
5.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是(　　)
A.60° B.50° C.40° D.30°
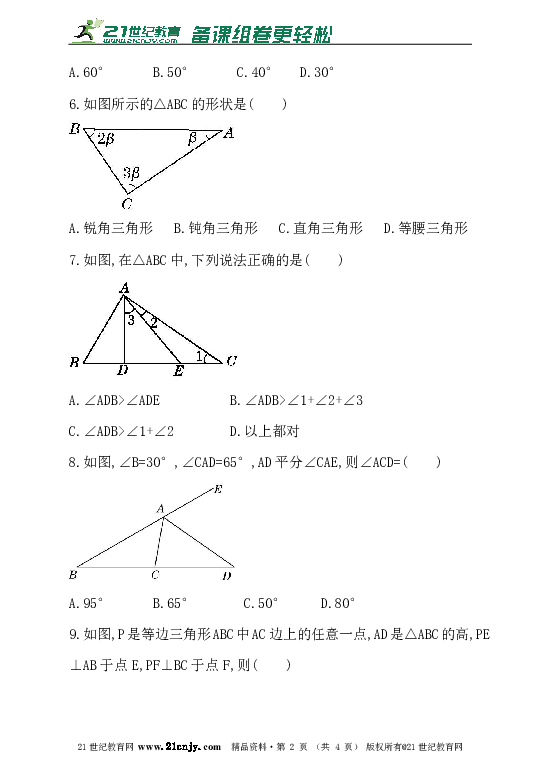
6.如图所示的△ABC的形状是(　　)
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
7.如图,在△ABC中,下列说法正确的是(　　)
A.∠ADB>∠ADE B.∠ADB>∠1+∠2+∠3
C.∠ADB>∠1+∠2 D.以上都对
8.如图,∠B=30°,∠CAD=65°,AD平分∠CAE,则∠ACD=(　　)
A.95° B.65° C.50° D.80°
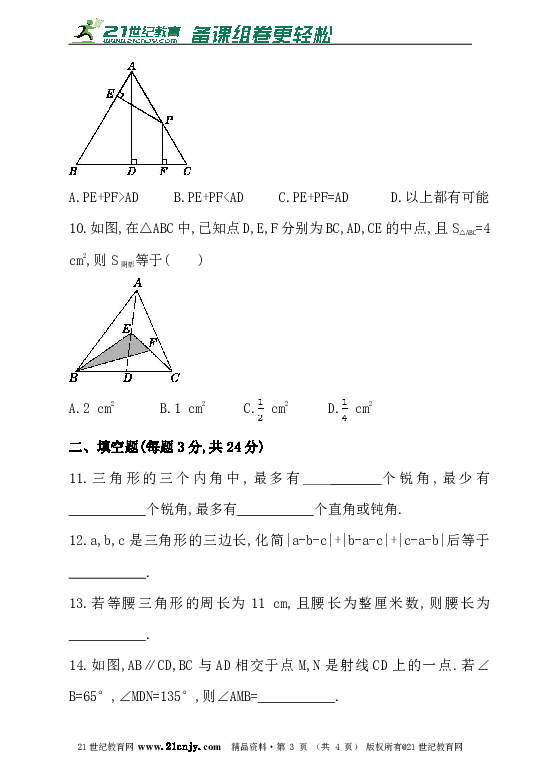
9.如图,P是等边三角形ABC中AC边上的任意一点,AD是△ABC的高,PE⊥AB于点E,PF⊥BC于点F,则(　　)21·cn·jy·com
A.PE+PF>AD B.PE+PF10.如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4 cm2,则S阴影等于(　　)21·世纪*教育网
A.2 cm2 B.1 cm2 C. cm2 D. cm2
二、填空题(每题3分,共24分)
11.三角形的三个内角中,最多有___________个锐角,最少有___________个锐角,最多有___________个直角或钝角.?
12.a,b,c是三角形的三边长,化简|a-b-c|+|b-a-c|+|c-a-b|后等于___________.21教育网
13.若等腰三角形的周长为11 cm,且腰长为整厘米数,则腰长为___________.?
14.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,则∠AMB=___________.21*cnjy*com
15.若一个三角形的三个内角的度数之比为1∶2∶3,则相对应的三个外角的度数之比为　　　　　.?
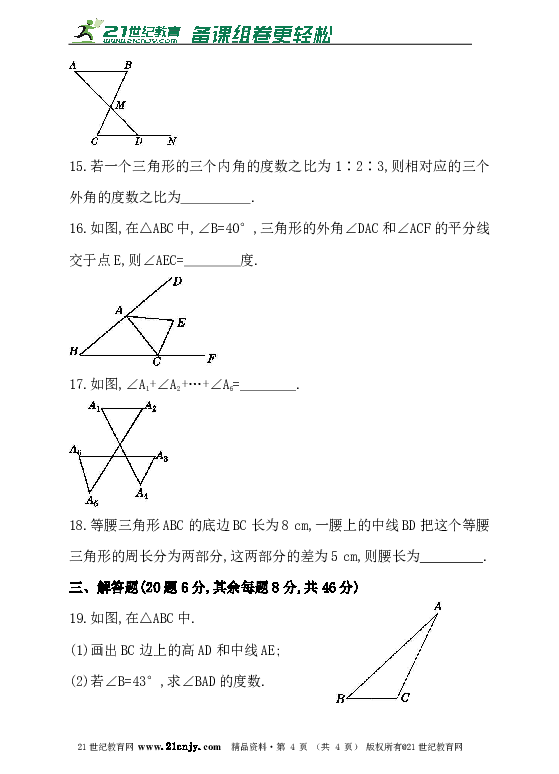
16.如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=　　　　度.【来源：21cnj*y.co*m】
17.如图,∠A1+∠A2+…+∠A6=　　　　.
18.等腰三角形ABC的底边BC长为8 cm,一腰上的中线BD把这个等腰三角形的周长分为两部分,这两部分的差为5 cm,则腰长为_________.
三、解答题(20题6分,其余每题8分,共46分)
19.如图,在△ABC中.
(1)画出BC边上的高AD和中线AE;
(2)若∠B=43°,求∠BAD的度数.
20.如图,小宇和小亮住在一起(A点),每天一块儿去学校(B点)上学.这天,小宇要先去文具店(C点)买圆规再去学校,小亮要先去书店(P点)买书再去学校,问这天两人从家到学校谁走的路远?为什么?
21.如图,已知AD∥BC,且AE,BE分别平分∠DAB,∠ABC,判断AE与BE的位置关系,并说明理由.www-2-1-cnjy-com
22.已知△ABC的高为AD,∠BAD=70°,∠CAD=20°,求∠BAC的度数.
23.如图,△ABC的角平分线BP,CP相交于点P,过点P作直线MN∥BC,分别交AB和AC于点M和N.若∠A=α,试用含α的代数式表示∠MPB+∠NPC的度数.若直线MN与BC不平行,上述结论仍成立吗?试说明理由.【出处：21教育名师】
24.如图,试探究∠BDC与∠A,∠B,∠C之间的关系.
参考答案
一、1.【答案】D　2.【答案】C　
3.【答案】A　
解：利用三角形内角和定理可求出第三个内角为180°-55°-65°=60°.根据三角形每个外角与和它相邻的内角互补,可求出三个外角分别为180°-55°=125°,180°-65°=115°,180°-60°=120°.故选A.
4.【答案】B　5.【答案】C
6.【答案】C　
解：根据三角形内角和定理,得β+2β+3β=180°,解得β=30°,所以三角形的三个内角的度数分别为30°,60°,90°,所以三角形为直角三角形.2·1·c·n·j·y
7.【答案】C　
解：由题图可知∠ADB=∠1+∠2+∠3,故∠ADB>∠1+∠2.
8.【答案】D　
解：因为AD平分∠CAE,所以∠CAD=∠EAD,所以∠EAC=65°×2=130°,所以∠BAC=180°-∠EAC=50°.根据三角形外角的性质,得∠ACD=∠B+∠BAC,所以∠ACD=30°+50°=80°.【版权所有：21教育】
9.【答案】C　
解：本题运用巧添辅助线法和等面积法.如图,连接BP,则S△ABC=S△ABP+S△CBP,即BC·AD=AB·PE+BC·PF.因为等边三角形的三边相等,所以PE+PF=AD.21cnjy.com
10.【答案】B　
解：S阴影=S△BCE=(S△BDE+S△CDE)=S△ABD+S△ACD=S△ABC=1cm2.
二、11.【答案】3;2;1
12.【答案】a+b+c　
解：|a-b-c|+|b-a-c|+|c-a-b|=|a-(b+c)|+|b-(a+c)|+|c-(a+b)|.因为三角形任意两边之和大于第三边,所以b+c>a,a+c>b,a+b>c,即a-(b+c)<0,b-(a+c)<0,c-(a+b)<0.所以|a-(b+c)|+|b-(a+c)|+|c-(a+b)|=(b+c)-a+(a+c)-b+(a+b)-c=a+b+c.
13.【答案】3 cm或4 cm或5 cm　
14.【答案】70°
15.【答案】5∶4∶3　
解：因为三个内角的度数之比为1∶2∶3,所以三个内角依次是30°,60°,90°,相对应的三个外角依次为150°,120°,90°.所以相对应的三个外角的度数之比为5∶4∶3.2-1-c-n-j-y
16.【答案】70　 17.【答案】360°
18.【答案】13 cm　
解：本题运用分类讨论思想和方程思想.设AD=CD=x cm,则AB=2x cm.当(AB+AD)-(BC+CD)=5 cm时,即2x+x-8-x=5,解得x=6.5,此时腰长为2×6.5=13(cm);当(BC+CD)-(AB+AD)=5 cm时,即8+x-2x-x=5,解得x=1.5,此时腰长为2×1.5=3(cm),因为3+3<8,所以腰长不可能为3 cm.所以腰长为13 cm.21教育名师原创作品
三、19.解:(1)如图所示.
(2)∵AD⊥BD,　∴∠D=90°.∵∠B=43°,∴∠BAD=90°-∠B=90°-43°=47°.21世纪教育网版权所有
20.解:小宇走的路远.因为小宇所走的路程为AC+BC,而BC=PC+BP,所以小宇所走的路程为AC+PC+BP.小亮所走的路程为AP+BP,在△ACP中,因为AC+PC>AP,所以小宇走的路远.21*cnjy*com
21.解:AE⊥BE.理由如下:
因为AD∥BC,
所以∠DAB+∠CBA=180°.
又因为AE,BE分别平分∠DAB与∠CBA,
所以∠BAE=∠BAD,∠ABE=∠CBA.
所以∠BAE+∠ABE=(∠BAD+∠CBA)=90°.
又因为∠BAE+∠ABE+∠AEB=180°,
所以∠AEB=180°-(∠BAE+∠ABE)=90°.
所以AE⊥BE.
22.解:(1)当垂足点D落在BC边上时,如图(1).∵∠BAD=70°,∠CAD=20°,
∴∠BAC=∠BAD+∠CAD=70°+20°=90°.
(2)当垂足点D落在BC的延长线上时,如图(2).
∵∠BAD=70°,∠CAD=20°,
∴∠BAC=∠BAD-∠CAD=70°-20°=50°.
综上所述,∠BAC的度数为90°或50°.
分析：由于AD为底边BC上的高,过点A作底边BC的垂线时,垂足点D可能落在BC边上,也可能落在BC的延长线上,因此,我们需要进行分类讨论.www.21-cn-jy.com
23.解:∵BP,CP分别平分∠ABC,∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB.
∵∠A=α,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-α,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=90°-α.
∵MN∥BC,
∴∠MPB=∠PBC,∠NPC=∠PCB,
∴∠MPB+∠NPC=∠PBC+∠PCB=90°-α.
若MN与BC不平行,上述结论仍成立.即:若MN与BC不平行,∠PBC+∠PCB仍为90°-α.
∵∠MPB+∠BPC+∠NPC=180°,
∠BPC+∠PBC+∠PCB=180°,
∴∠MPB+∠NPC=180°-∠BPC=180°-[180°-(∠PBC+∠PCB)]=∠PBC+∠PCB=90°-α.
分析：本题运用了整体思想.尤其当MN与BC不平行时,利用整体代换更能体现∠PBC+∠PCB与∠A的恒定关系.
24.解:如图,延长BD交AC于点E.因为∠BDC是△CED的一个外角,所以∠BDC=∠C+∠CED.又因为∠CED是△ABE的一个外角,所以∠CED=∠A+∠B.所以∠BDC=∠A+∠B+∠C.【来源：21·世纪·教育·网】