第二章相交线与平行线单元检测题A

第二章《相交线与平行线》单元检测题A
一．选择题（共12小题）
1．（2016?常州）已知△ABC中，BC=6，AC=3，CP⊥AB，垂足为P，则CP的长可能是（　　）【来源：21cnj*y.co*m】
A．2 B．4 C．5 D．7
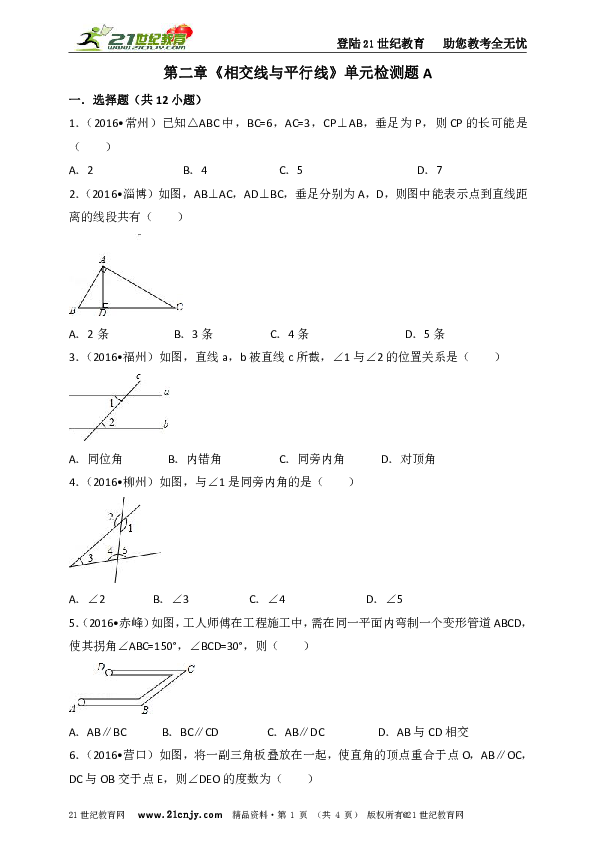
2．（2016?淄博）如图，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有（　　）
A．2条 B．3条 C．4条 D．5条
3．（2016?福州）如图，直线a，b被直线c所截，∠1与∠2的位置关系是（　　）
A．同位角 B．内错角 C．同旁内角 D．对顶角
4．（2016?柳州）如图，与∠1是同旁内角的是（　　）
A．∠2 B．∠3 C．∠4 D．∠5
5．（2016?赤峰）如图，工人师傅在工程施工中，需在同一平面内弯制一个变形管道ABCD，使其拐角∠ABC=150°，∠BCD=30°，则（　　）21教育名师原创作品
A．AB∥BC B．BC∥CD C．AB∥DC D．AB与CD相交
6．（2016?营口）如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为（　　）
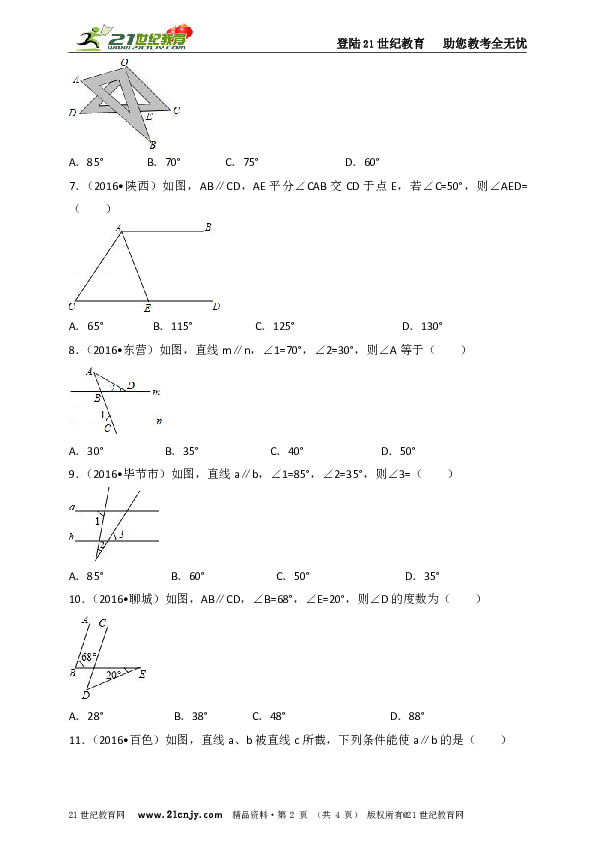
A．85° B．70° C．75° D．60°
7．（2016?陕西）如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=50°，则∠AED=（　　）21*cnjy*com
A．65° B．115° C．125° D．130°
8．（2016?东营）如图，直线m∥n，∠1=70°，∠2=30°，则∠A等于（　　）
A．30° B．35° C．40° D．50°
9．（2016?毕节市）如图，直线a∥b，∠1=85°，∠2=35°，则∠3=（　　）
A．85° B．60° C．50° D．35°
10．（2016?聊城）如图，AB∥CD，∠B=68°，∠E=20°，则∠D的度数为（　　）
A．28° B．38° C．48° D．88°
11．（2016?百色）如图，直线a、b被直线c所截，下列条件能使a∥b的是（　　）
A．∠1=∠6 B．∠2=∠6 C．∠1=∠3 D．∠5=∠7
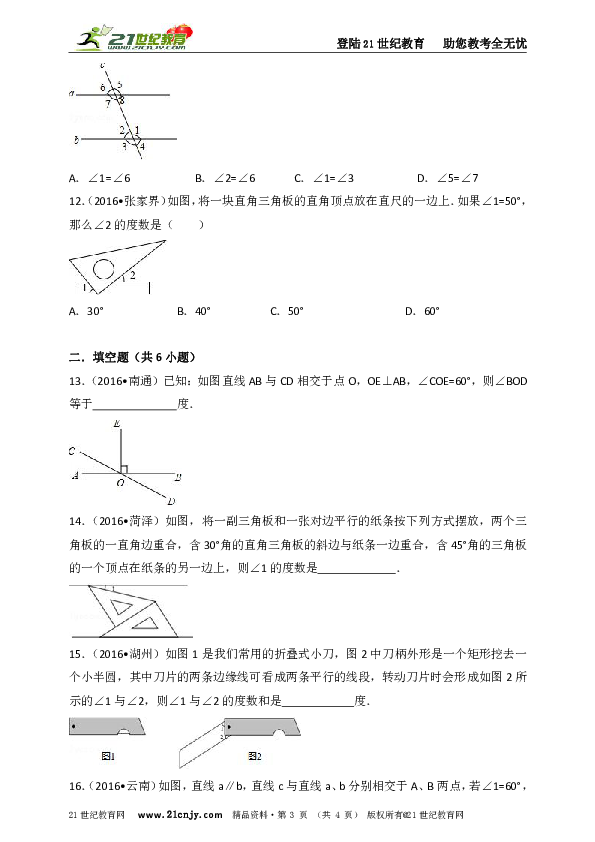
12．（2016?张家界）如图，将一块直角三角板的直角顶点放在直尺的一边上．如果∠1=50°，那么∠2的度数是（　　）
A．30° B．40° C．50° D．60°
　
二．填空题（共6小题）
13．（2016?南通）已知：如图直线AB与CD相交于点O，OE⊥AB，∠COE=60°，则∠BOD等于　 　度．
14．（2016?菏泽）如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是　 　．
15．（2016?湖州）如图1是我们常用的折叠式小刀，图2中刀柄外形是一个矩形挖去一个小半圆，其中刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图2所示的∠1与∠2，则∠1与∠2的度数和是　 　度．
16．（2016?云南）如图，直线a∥b，直线c与直线a、b分别相交于A、B两点，若∠1=60°，则∠2=　 　．21教育网
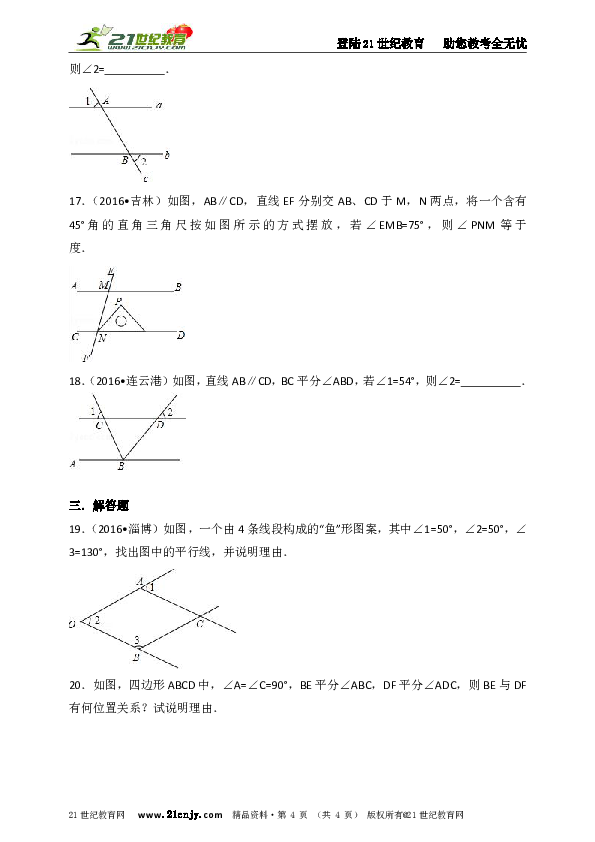
17．（2016?吉林）如图，AB∥CD，直线EF分别交AB、CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于　 　度．
18．（2016?连云港）如图，直线AB∥CD，BC平分∠ABD，若∠1=54°，则∠2=　 　．
　
三．解答题
19．（2016?淄博）如图，一个由4条线段构成的“鱼”形图案，其中∠1=50°，∠2=50°，∠3=130°，找出图中的平行线，并说明理由．www-2-1-cnjy-com
20．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠ADC，则BE与DF有何位置关系？试说明理由．
21．如图，AB∥CD，直线EF交AB、CD于点G、H．如果GM平分∠BGF，HN平分∠CHE，那么GM与HN平行吗？为什么？
22．如图，已知AC∥ED，AB∥FD，∠A=65°，求：∠EDF的度数．
23．如图，直线a∥b，BC平分∠ABD，DE⊥BC，若∠1=70°，求∠2的度数．
24．如图，已知AB∥CD，若∠C=40°，∠E=20°，求∠A的度数．
25．（2016?广州）如图，利用尺规，在△ABC的边AC上方作∠CAE=∠ACB，在射线AE上截取AD=BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法）
　
参考答案与解析
一．选择题
1．【分析】根据垂线段最短得出结论．
解：如图，根据垂线段最短可知：PC＜3，
∴CP的长可能是2，
故选A．
　
2．【分析】直接利用点到直线的距离的定义分析得出答案．
解：如图所示：线段AB是点B到AC的距离，
线段CA是点C到AB的距离，
线段AD是点A到BC的距离，
线段BD是点B到AD的距离，
线段CD是点C到AD的距离，
故图中能表示点到直线距离的线段共有5条．
故选：D．
　
3．【分析】根据内错角的定义求解．
解：直线a，b被直线c所截，∠1与∠2是内错角．
故选B．
　
4．【分析】根据同位角、内错角、同旁内角、对顶角的定义逐个判断即可．
解：A、∠1和∠2是对顶角，不是同旁内角，故本选项错误；
B、∠1和∠3是同位角，不是同旁内角，故本选项错误；
C、∠1和∠4是内错角，不是同旁内角，故本选项错误；
D、∠1和∠5是同旁内角，故本选项正确；
故选D．
　
5．【分析】根据同旁内角互补，两直线平行即可求解．
解：∵∠ABC=150°，∠BCD=30°，
∴∠ABC+∠BCD=180°，
∴AB∥DC．
故选：C．
　
6．【分析】由平行线的性质求出∠AOC=120°，再求出∠BOC=30°，然后根据三角形的外角性质即可得出结论．21世纪教育网版权所有
解：∵AB∥OC，∠A=60°，
∴∠A+∠AOC=180°，
∴∠AOC=120°，
∴∠BOC=120°﹣90°=30°，
∴∠DEO=∠C+∠BOC=45°+30°=75°；
故选：C．
　
7．【分析】根据平行线性质求出∠CAB的度数，根据角平分线求出∠EAB的度数，根据平行线性质求出∠AED的度数即可．2-1-c-n-j-y
解：∵AB∥CD，
∴∠C+∠CAB=180°，
∵∠C=50°，
∴∠CAB=180°﹣50°=130°，
∵AE平分∠CAB，
∴∠EAB=65°，
∵AB∥CD，
∴∠EAB+∠AED=180°，
∴∠AED=180°﹣65°=115°，
故选B．
　
8．【分析】首先根据平行线的性质求出∠3的度数，然后根据三角形的外角的知识求出∠A的度数．
解：如图，∵直线m∥n，
∴∠1=∠3，
∵∠1=70°，
∴∠3=70°，
∵∠3=∠2+∠A，∠2=30°，
∴∠A=40°，
故选C．
　
9．【分析】先利用三角形的外角定理求出∠4的度数，再利用平行线的性质得∠3=∠4=50°．
解：在△ABC中，
∵∠1=85°，∠2=35°，
∴∠4=85°﹣35°=50°，
∵a∥b，
∴∠3=∠4=50°，
故选C．
　
10．【分析】根据平行线的性质得到∠1=∠B=68°，由三角形的外角的性质即可得到结论．
解：如图，∵AB∥CD，
∴∠1=∠B=68°，
∵∠E=20°，
∴∠D=∠1﹣∠E=48°，
故选C．
　
11．【分析】利用平行线的判定方法判断即可．
解：∵∠2=∠6（已知），
∴a∥b（同位角相等，两直线平行），
则能使a∥b的条件是∠2=∠6，
故选B
　
12．【分析】由两直线平行，同位角相等，可求得∠3的度数，然后求得∠2的度数．
解：如图，
，
∵∠1=50°，
∴∠3=∠1=50°，
∴∠2=90°﹣50°=40°．
故选B．
　
二．填空题
13．【分析】根据垂线的定义，可得∠ACE的度数，根据余角的性质，可得∠AOC的度数，根据对顶角相等，可得答案．www.21-cn-jy.com
解：由垂线的定义，得
∠AOE=90°，
由余角的性质，得
∠AOC=∠AOE﹣∠COE=30°，
由对顶角相等，得
∠BOD=∠AOC=30°，
故答案为：30．
　
14．【分析】过A点作AB∥a，利用平行线的性质得AB∥b，所以∠1=∠2，∠3=∠4=30°，加上∠2+∠3=45°，易得∠1=15°．21·世纪*教育网
解：如图，过A点作AB∥a，
∴∠1=∠2，
∵a∥b，
∴AB∥b，
∴∠3=∠4=30°，
而∠2+∠3=45°，
∴∠2=15°，
∴∠1=15°．
故答案为15°．
　
15．【分析】如图2，AB∥CD，∠AEC=90°，作EF∥AB，根据平行线的传递性得到EF∥CD，则根据平行线的性质得∠1=∠AEF，∠2=∠CEF，所以∠1+∠2=∠AEC=90°
解：如图2，AB∥CD，∠AEC=90°，
作EF∥AB，则EF∥CD，
所以∠1=∠AEF，∠2=∠CEF，
所以∠1+∠2=∠AEF+∠CEF=∠AEC=90°．
故答案为90．
　
16．【分析】先根据平行线的性质求出∠3的度数，再由对顶角的定义即可得出结论．
解：∵直线a∥b，∠1=60°，
∴∠1=∠3=60°．
∵∠2与∠3是对顶角，
∴∠2=∠3=60°．
故答案为：60°．
　
17．【分析】根据平行线的性质得到∠DNM=∠BME=75°，由等腰直角三角形的性质得到∠PND=45°，即可得到结论．【来源：21·世纪·教育·网】
解：∵AB∥CD，
∴∠DNM=∠BME=75°，
∵∠PND=45°，
∴∠PNM=∠DNM﹣∠DNP=30°，
故答案为：30．
　
18．【分析】由AB∥CD，根据平行线的性质找出∠ABC=∠1，由BC平分∠ABD，根据角平分线的定义即可得出∠CBD=∠ABC，再结合三角形的内角和为180°以及对顶角相等即可得出结论．2·1·c·n·j·y
解：∵AB∥CD，∠1=54°，
∴∠ABC=∠1=54°，
又∵BC平分∠ABD，
∴∠CBD=∠ABC=54°．
∵∠CBD+∠BDC+∠DCB=180°，∠1=∠DCB，∠2=∠BDC，
∴∠2=180°﹣∠1﹣∠CBD=180°﹣54°﹣54°=72°．
故答案为：72°．
　
三．解答题
19．【分析】根据同位角相等，两直线平行证明OB∥AC，根据同旁内角互补，两直线平行证明OA∥BC．21*cnjy*com
解：OA∥BC，OB∥AC．
∵∠1=50°，∠2=50°，
∴∠1=∠2，
∴OB∥AC，
∵∠2=50°，∠3=130°，
∴∠2+∠3=180°，
∴OA∥BC．
　
20．【分析】根据四边形的内角和定理和∠A=∠C=90°，得∠ABC+∠ADC=180°；根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等，从而证明两条直线平行．【版权所有：21教育】
解：BE∥DF．理由如下：
∵∠A=∠C=90°（已知），
∴∠ABC+∠ADC=180°（四边形的内角和等于360°）．
∵BE平分∠ABC，DF平分∠ADC，
∴∠1=∠2=∠ABC，∠3=∠4=∠ADC（角平分线的定义）．
∴∠1+∠3=（∠ABC+∠ADC）=×180°=90°（等式的性质）．
又∠1+∠AEB=90°（三角形的内角和等于180°），
∴∠3=∠AEB（同角的余角相等）．
∴BE∥DF（同位角相等，两直线平行）．
　
21．【分析】首先根据平行线的性质可得∠BGF=∠CHE，再根据角平分线的性质可证明∠NHG=∠MGH，然后根据内错角相等，两直线平行可得HN∥GM．
解：GM与HN平行．
∵AB∥CD，
∴∠BGF=∠CHE，
∵GM平分∠BGF，
∴∠MGH=∠BGF，
同理，∠NHG=∠CHE，
∴∠CHE=∠BGF，
∴∠NHG=∠MGH，
∴HN∥GM．
　
22．【分析】根据平行线的性质，即可解答．
解：∵AC∥ED，
∴∠BED=∠A=65°，
∵AB∥FD，
∴∠EDF=∠BED=65°．
　
23．【分析】根据平行线的性质得到∠1=∠ABD=70°，由角平分线的定义得到∠EBD=ABD=35°，根据三角形的内角和即可得到结论．21cnjy.com
解：∵直线a∥b，
∴∠1=∠ABD=70°，
∵BC平分∠ABD，
∴∠EBD=ABD=35°，
∵DE⊥BC，
∴∠2=90°﹣∠EBD=55°．
　
24．【分析】根据两直线平行，同位角相等可得∠1=∠C，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．21·cn·jy·com
解：如图，∵AB∥CD，
∴∠1=∠C=40°，
∴∠A=∠1﹣∠E=40°﹣20°=20°．
　
25．【分析】利用尺规作∠EAC=∠ACB即可，先证明四边形ABCD是平行四边形，再证明CD∥AB即可．【出处：21教育名师】
解：图象如图所示，
∵∠EAC=∠ACB，
∴AD∥CB，
∵AD=BC，
∴四边形ABCD是平行四边形，
∴AB∥CD．