7.5.1 平行线的性质 同步练习

7.5.1 平行线的性质
基础训练
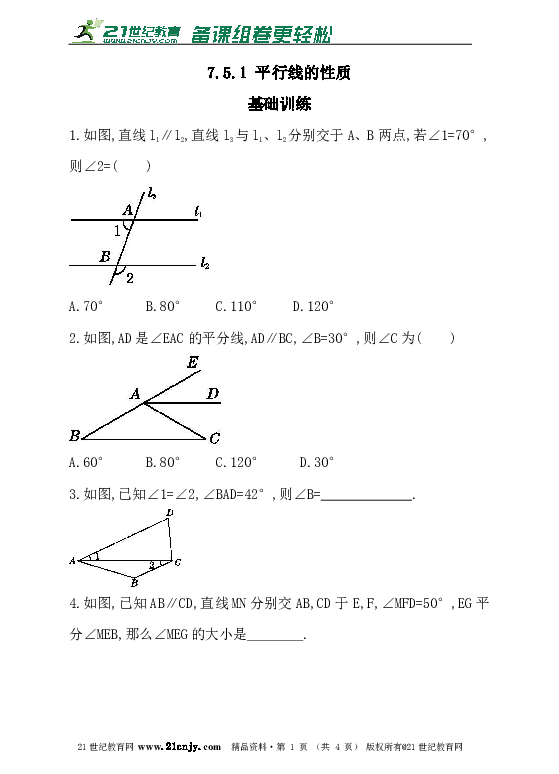
1.如图,直线l1∥l2,直线l3与l1、l2分别交于A、B两点,若∠1=70°,则∠2=(　　)
A.70° B.80° C.110° D.120°
2.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为(　　)
A.60° B.80° C.120° D.30°
3.如图,已知∠1=∠2,∠BAD=42°,则∠B=_____________.
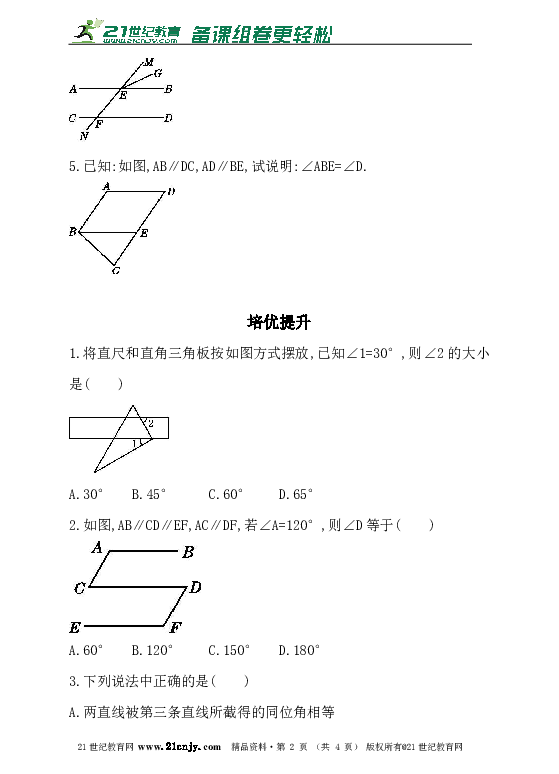
4.如图,已知AB∥CD,直线MN分别交AB,CD于E,F,∠MFD=50°,EG平分∠MEB,那么∠MEG的大小是　　　　.21世纪教育网版权所有
5.已知:如图,AB∥DC,AD∥BE,试说明:∠ABE=∠D.
培优提升
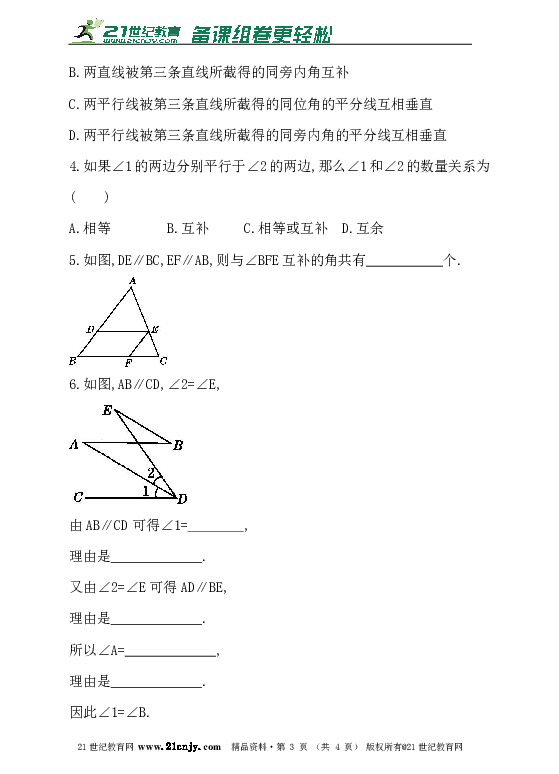
1.将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是(　　)
A.30° B.45° C.60° D.65°
2.如图,AB∥CD∥EF,AC∥DF,若∠A=120°,则∠D等于(　　)
A.60° B.120° C.150° D.180°
3.下列说法中正确的是(　　)
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
4.如果∠1的两边分别平行于∠2的两边,那么∠1和∠2的数量关系为(　　)
A.相等 B.互补 C.相等或互补 D.互余
5.如图,DE∥BC,EF∥AB,则与∠BFE互补的角共有___________个.?
6.如图,AB∥CD,∠2=∠E,
由AB∥CD可得∠1=　　　　,?
理由是_____________.
又由∠2=∠E可得AD∥BE,
理由是_____________.?
所以∠A=_____________,?
理由是_____________.?
因此∠1=∠B.
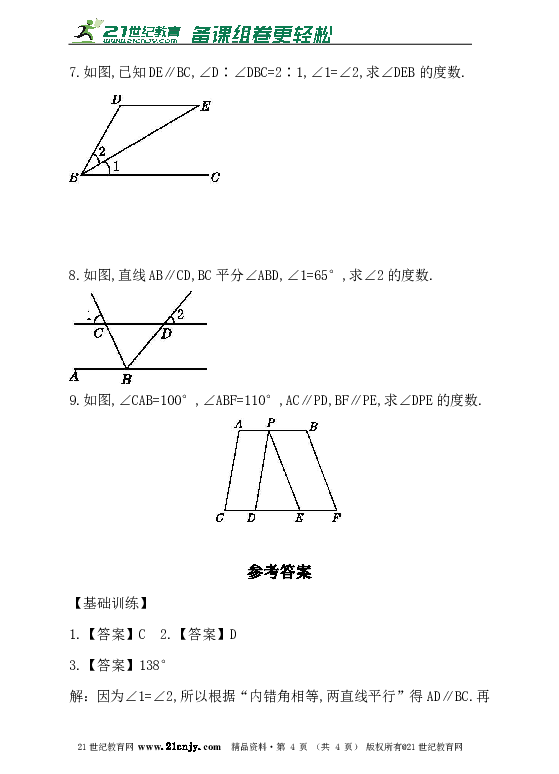
7.如图,已知DE∥BC,∠D∶∠DBC=2∶1,∠1=∠2,求∠DEB的度数.
8.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
9.如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.
参考答案
【基础训练】
1.【答案】C　2.【答案】D
3.【答案】138°　
解：因为∠1=∠2,所以根据“内错角相等,两直线平行”得AD∥BC.再根据“两直线平行,同旁内角互补”得∠B=180°-∠BAD=180°-42°=138°.21cnjy.com
4.【答案】25°
解：由AB∥CD,得∠MEB=∠MFD=50°.由EG平分∠MEB,得∠MEG=∠
MEB=25°.
5.解:∵AB∥DC(已知),∴∠ABE=∠BEC(两直线平行,内错角相等).∵AD∥BE(已知),∴∠D=∠BEC(两直线平行,同位角相等).∴∠ABE=∠D(等量代换).21·cn·jy·com
【培优提升】
1.【答案】C
2.【答案】A　
解：∵AB∥CD,∴∠A+∠C=180°,∴∠C=180°-∠A=60°.又∵AC∥DF,∴∠D=∠C=60°.www.21-cn-jy.com
3.【答案】D　
解：对于A,B两选项,只有在两直线平行的前提下才会成立.对于C选项,如图(1):BC∥EF,BD平分∠ABC,EH平分∠BEF,2·1·c·n·j·y
(1)
(2)
则∠ABD=∠BEH.
∴BD∥EH.C选项错.
对于D选项,如图(2),BC∥EF,BD平分∠EBC,
ED平分∠BEF,
则2∠1+2∠2=180°,
∴∠1+∠2=90°,
即:△BDE为直角三角形,
∴BD⊥DE.
4.【答案】C　
解：本题运用了分类讨论思想.此题易分析不全情况而错选A或B.根据题目中的条件,这两个角的关系有两种情况,如图所示,故选C.
5.【答案】4　
解：从题图中可以看出有∠B,∠EFC,∠DEF,∠ADE共4个角与∠BFE互补.
6.【答案】∠A;两直线平行,内错角相等;内错角相等,两直线平行;∠B;两直线平行,内错角相等
7.解:∵DE∥BC(已知),∴∠D+∠DBC=180°(两直线平行,同旁内角互补).又∵∠D∶∠DBC=2∶1,∴∠DBC=60°.∵∠DBC=∠1+∠2,∠1=∠2(已知),∴∠1=30°.∵DE∥BC(已知),∴∠DEB=∠1(两直线平行,内错角相等),∴∠DEB=30°.21教育网
解：题图中BD和BE都可作为平行线DE,BC的截线,由此可得∠DEB=∠1,∠D+∠1+∠2=180°,再结合已知条件便可求得∠DEB的度数.
8.解:∵AB∥CD,
∴∠ABC=∠1=65°,∠ABD+∠BDC=180°.
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠BDC=180°-∠ABD=50°,
∴∠2=∠BDC=50°.
9.解法一:∵AC∥PD,∴∠CAB+∠APD=180°.∵∠CAB=100°,∴∠APD=180°-∠CAB=180°-100°=80°.同理可求得∠BPE=70°.∴∠DPE=180°-∠APD-∠BPE=180°-80°-70°=30°.【来源：21·世纪·教育·网】
解法二:∵AC∥PD,∴∠DPB=∠CAB=100°.∵BF∥PE,∴∠ABF+∠BPE=180°.∵∠ABF=110°,∴∠BPE=180°-∠21·世纪*教育网
ABF=180°-110°=70°.∴∠DPE=∠DPB-∠BPE=100°-70°=30°.
分析：对于解法一,由AC∥PD,可以得出∠CAB+∠APD=180°.又知∠CAB的度数,即可求出∠APD的度数.同理可以求出∠BPE的度数,再由平角的定义求出∠DPE的度数.www-2-1-cnjy-com