6.2.1 代入消元法(一) 同步练习
文档属性
| 名称 | 6.2.1 代入消元法(一) 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 386.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-23 08:46:22 | ||
图片预览
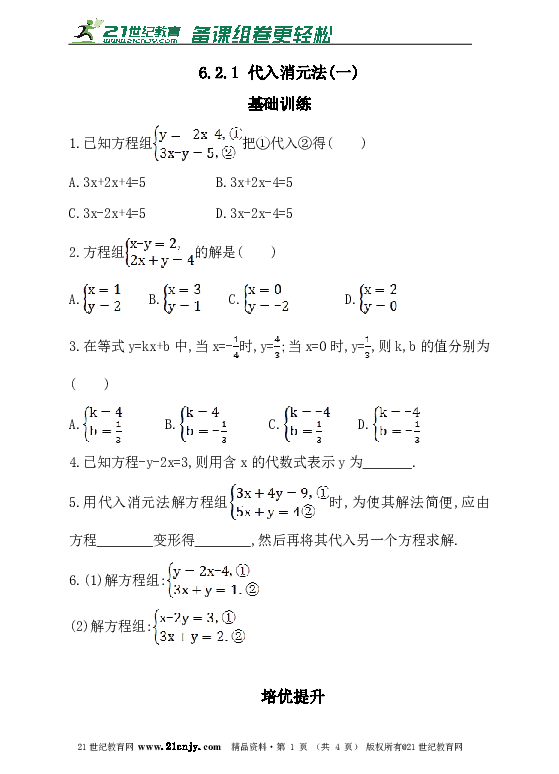
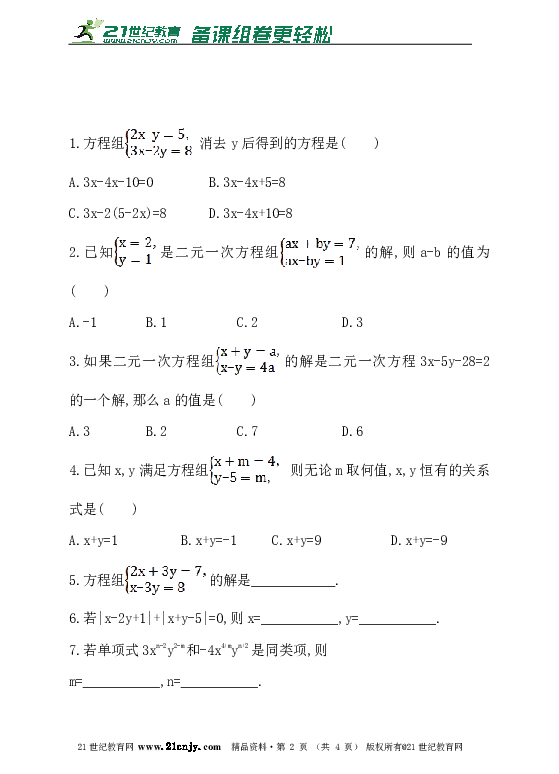


文档简介
6.2.1 代入消元法(一)
基础训练
1.已知方程组把①代入②得( )
A.3x+2x+4=5 B.3x+2x-4=5
C.3x-2x+4=5 D.3x-2x-4=5
2.方程组的解是( )
A. B. C. D.
3.在等式y=kx+b中,当x=-时,y=;当x=0时,y=,则k,b的值分别为( )
A. B. C. D.
4.已知方程-y-2x=3,则用含x的代数式表示y为_______.
5.用代入消元法解方程组时,为使其解法简便,应由方程________变形得________,然后再将其代入另一个方程求解.?
6.(1)解方程组:
(2)解方程组:
培优提升
1.方程组 消去y后得到的方程是( )
A.3x-4x-10=0 B.3x-4x+5=8
C.3x-2(5-2x)=8 D.3x-4x+10=8
2.已知是二元一次方程组的解,则a-b的值为( )
A.-1 B.1 C.2 D.3
3.如果二元一次方程组的解是二元一次方程3x-5y-28=2的一个解,那么a的值是( )
A.3 B.2 C.7 D.6
4.已知x,y满足方程组 则无论m取何值,x,y恒有的关系式是( )
A.x+y=1 B.x+y=-1 C.x+y=9 D.x+y=-9
5.方程组的解是____________.
6.若|x-2y+1|+|x+y-5|=0,则x=___________,y=___________.
7.若单项式3xn-2y2-m和-4x4+myn+2是同类项,则
m=___________,n=___________.
8.(1)解方程组
(2)解方程组
参考答案
【基础训练】
1.【答案】A
2.【答案】D
解:将x-y=2变形得x=2+y,将x=2+y代入2x+y=4得:2(2+y)+y=4,解得y=0.所以x=2+y=2.21教育网
3.【答案】C
解:将x=-,y=代入方程得=-k+b;将x=0,y=代入方程得=0+b.
解方程组得
4.【答案】y=-2x-3 5.【答案】②;y=4-5x
6.解:(1)把①代入②,得3x+2x-4=1,x=1,
把x=1代入①,得y=-2,
所以这个方程组的解是
(2)由①,得x=2y+3,③
把③代入②,得3(2y+3)+y=2,解得y=-1,
把y=-1代入③,得x=1,所以这个方程组的解是
【培优提升】
1.【答案】D
解:将2x-y=5变形得y=2x-5,将y=2x-5代入3x-2y=8,得3x-2(2x-5)=8,整理得:3x-4x+10=8.21世纪教育网版权所有
2.【答案】A
解:将代入方程组,
得解得所以a-b=-1.
3.【答案】B
解:解方程组得
将x=a,y=-a代入3x-5y-28=2,得3×a-5×-28=2,解得a=2.
4.【答案】C
解:将m=y-5代入x+m=4,得x+y-5=4,整理得x+y=9.
5.【答案】
6.【答案】3;2
解:方程思想是指在求解数学问题时,从题中的已知量和未知量之间的数量关系入手,找出数量关系,列出方程(组),再通过解方程(组)使问题获得解决,本题运用方程思想解答.因为|x-2y+1|≥0,|x+y-5|≥0,且|x-2y+1|+|x+y-5|=0,所以解得
7.【答案】-3;3
解:因为两个单项式是同类项,所以解得
8.解:(1)由①得y=4-2x,③
将③代入②,得
2(4-2x)+1=5x,
解得x=1.
将x=1代入③,得
y=2.
所以原方程组的解为
(2)
由②得x=5-y,③
将③代入①,得
5(5-y)-2y-4=0,
解得y=3.
将y=3代入③,得x=2.
所以原方程组的解为
基础训练
1.已知方程组把①代入②得( )
A.3x+2x+4=5 B.3x+2x-4=5
C.3x-2x+4=5 D.3x-2x-4=5
2.方程组的解是( )
A. B. C. D.
3.在等式y=kx+b中,当x=-时,y=;当x=0时,y=,则k,b的值分别为( )
A. B. C. D.
4.已知方程-y-2x=3,则用含x的代数式表示y为_______.
5.用代入消元法解方程组时,为使其解法简便,应由方程________变形得________,然后再将其代入另一个方程求解.?
6.(1)解方程组:
(2)解方程组:
培优提升
1.方程组 消去y后得到的方程是( )
A.3x-4x-10=0 B.3x-4x+5=8
C.3x-2(5-2x)=8 D.3x-4x+10=8
2.已知是二元一次方程组的解,则a-b的值为( )
A.-1 B.1 C.2 D.3
3.如果二元一次方程组的解是二元一次方程3x-5y-28=2的一个解,那么a的值是( )
A.3 B.2 C.7 D.6
4.已知x,y满足方程组 则无论m取何值,x,y恒有的关系式是( )
A.x+y=1 B.x+y=-1 C.x+y=9 D.x+y=-9
5.方程组的解是____________.
6.若|x-2y+1|+|x+y-5|=0,则x=___________,y=___________.
7.若单项式3xn-2y2-m和-4x4+myn+2是同类项,则
m=___________,n=___________.
8.(1)解方程组
(2)解方程组
参考答案
【基础训练】
1.【答案】A
2.【答案】D
解:将x-y=2变形得x=2+y,将x=2+y代入2x+y=4得:2(2+y)+y=4,解得y=0.所以x=2+y=2.21教育网
3.【答案】C
解:将x=-,y=代入方程得=-k+b;将x=0,y=代入方程得=0+b.
解方程组得
4.【答案】y=-2x-3 5.【答案】②;y=4-5x
6.解:(1)把①代入②,得3x+2x-4=1,x=1,
把x=1代入①,得y=-2,
所以这个方程组的解是
(2)由①,得x=2y+3,③
把③代入②,得3(2y+3)+y=2,解得y=-1,
把y=-1代入③,得x=1,所以这个方程组的解是
【培优提升】
1.【答案】D
解:将2x-y=5变形得y=2x-5,将y=2x-5代入3x-2y=8,得3x-2(2x-5)=8,整理得:3x-4x+10=8.21世纪教育网版权所有
2.【答案】A
解:将代入方程组,
得解得所以a-b=-1.
3.【答案】B
解:解方程组得
将x=a,y=-a代入3x-5y-28=2,得3×a-5×-28=2,解得a=2.
4.【答案】C
解:将m=y-5代入x+m=4,得x+y-5=4,整理得x+y=9.
5.【答案】
6.【答案】3;2
解:方程思想是指在求解数学问题时,从题中的已知量和未知量之间的数量关系入手,找出数量关系,列出方程(组),再通过解方程(组)使问题获得解决,本题运用方程思想解答.因为|x-2y+1|≥0,|x+y-5|≥0,且|x-2y+1|+|x+y-5|=0,所以解得
7.【答案】-3;3
解:因为两个单项式是同类项,所以解得
8.解:(1)由①得y=4-2x,③
将③代入②,得
2(4-2x)+1=5x,
解得x=1.
将x=1代入③,得
y=2.
所以原方程组的解为
(2)
由②得x=5-y,③
将③代入①,得
5(5-y)-2y-4=0,
解得y=3.
将y=3代入③,得x=2.
所以原方程组的解为
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
