6.2.3 加减消元法 同步练习
图片预览


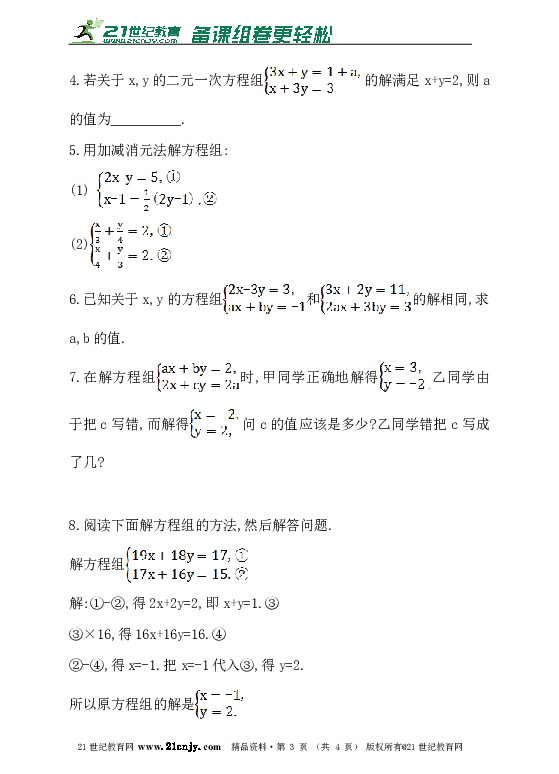

文档简介
6.2.3 加减消元法
基础训练
1.已知二元一次方程组用方程①减去方程②,得( )
A.2y=-2 B.2y=-36 C.12y=-2 D.12y=2
2.用加减消元法解方程组时,要使其中一个未知数的系数相同或互为相反数,必须适当变形,以下四种变形中正确的是( )
① ②
③ ④
A.①② B.③④ C.①④ D.②④
3.若x,y满足方程组则x-y的值等于( )
A.-1 B.1 C.2 D.3
4.若|x-2y-1|+(2x-y-5)2=0,则x+y=_____________.
5.解方程组:
(1)
(2)
(3)
培优提升
1.利用加减消元法解方程组下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
2.用加减消元法解方程组解法如下:
解:(1)①×2,②×3,得
(2)③-④,得y=-5.
(3)把y=-5代入②,得x=11.
(4)所以原方程组的解是
以上解题过程中,开始出错的一步是( )
A.(1) B.(2) C.(3) D.(4)
3.若|x-y-2|+(x+3y+10)2=0,则的值为( )
A. B.- C. D.-
4.若关于x,y的二元一次方程组的解满足x+y=2,则a的值为__________.
5.用加减消元法解方程组:
(1)
(2)
6.已知关于x,y的方程组和的解相同,求a,b的值.
7.在解方程组时,甲同学正确地解得乙同学由于把c写错,而解得问c的值应该是多少?乙同学错把c写成了几?21世纪教育网版权所有
8.阅读下面解方程组的方法,然后解答问题.
解方程组
解:①-②,得2x+2y=2,即x+y=1.③
③×16,得16x+16y=16.④
②-④,得x=-1.把x=-1代入③,得y=2.
所以原方程组的解是
(1)请你仿照上面的解法解方程组
(2)请大胆猜测关于x,y的方程组
(a≠b)的解.
参考答案
【基础训练】
1.【答案】D 2.【答案】B 3.【答案】A
4.【答案】4
解:由题意可得方程组
①×2得:2x-4y-2=0③,③-②得-3y+3=0,解得y=1,代入①解得:x=3.所以原方程组的解为所以x+y=4.
5.解:(1)①+②得:3x=15,所以x=5.
将x=5代入①,得:5+y=6,所以y=1,所以方程组的解为
(2)②×3,得3x+9y=21,③
③-①,得11y=22.所以y=2.
把y=2代入②,得x+6=7,所以x=1,所以原方程组的解为
(3)①×3+②,得10x=20,解得x=2.
把x=2代入①,得6-y=7,解得y=-1.所以原方程组的解为
分析:解二元一次方程组的基本思想是消元,基本方法有代入法和加减法. 当其中一个未知数的系数是1或-1时,用代入法简单;当同一未知数的系数相等、互为相反数或绝对值成整数关系时,用加减法简单.
【培优提升】
1.【答案】D 2.【答案】A
3.【答案】A
解:由题意得方程组
解得所以=.
4.【答案】4
解:本题运用整体思想解答.把x+y看成一个整体,可使问题简单化. ①+②,得4x+4y=a+4,x+y=.又因为x+y=2,所以=2,解得a=4.21教育网
5.解:(1)由②得:x-y=,③
①-③得:x=.
将x=代入③得:y=4.
所以这个方程组的解是
(2)①×36得,12x+9y=72 ③,②×48得,12x+16y=96 ④,④-③,得7y=24,解得y=.将y=代入①,解得x=.所以原方程组的解为21cnjy.com
6.解:解方程组得将其代入ax+by=-1,2ax+3by=3,可得①×2-②,得-b=-5,所以b=5.把b=5代入①,得a=-2.所以a,b的值分别为-2,5.21·cn·jy·com
分析:既然两个方程组的解相同,那么两个方程组的解也应与方程组的解相同,将此方程组的解代入含有a,b的两个方程中,得到关于a,b的二元一次方程组,从而求出a,b的值.
7.解:由题意,得设乙同学错把c写为c',则
所以解得a=4.
把a=4分别代入①,②,得6-2c=2×4,-4+2c'=2×4,所以c=-1,c'=6.所以c的值为-1,乙同学错把c写成了6.www.21-cn-jy.com
8.解:(1)①-②,得2x+2y=2,即x+y=1③.③×2 014,得2 014x+2 014y=2 014④.②-④,得x=-1.把x=-1代入③,得y=2.所以原方程组的解是2·1·c·n·j·y
(2)
分析:观察例题中方程组的特点找出规律,利用此规律解方程组.
基础训练
1.已知二元一次方程组用方程①减去方程②,得( )
A.2y=-2 B.2y=-36 C.12y=-2 D.12y=2
2.用加减消元法解方程组时,要使其中一个未知数的系数相同或互为相反数,必须适当变形,以下四种变形中正确的是( )
① ②
③ ④
A.①② B.③④ C.①④ D.②④
3.若x,y满足方程组则x-y的值等于( )
A.-1 B.1 C.2 D.3
4.若|x-2y-1|+(2x-y-5)2=0,则x+y=_____________.
5.解方程组:
(1)
(2)
(3)
培优提升
1.利用加减消元法解方程组下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
2.用加减消元法解方程组解法如下:
解:(1)①×2,②×3,得
(2)③-④,得y=-5.
(3)把y=-5代入②,得x=11.
(4)所以原方程组的解是
以上解题过程中,开始出错的一步是( )
A.(1) B.(2) C.(3) D.(4)
3.若|x-y-2|+(x+3y+10)2=0,则的值为( )
A. B.- C. D.-
4.若关于x,y的二元一次方程组的解满足x+y=2,则a的值为__________.
5.用加减消元法解方程组:
(1)
(2)
6.已知关于x,y的方程组和的解相同,求a,b的值.
7.在解方程组时,甲同学正确地解得乙同学由于把c写错,而解得问c的值应该是多少?乙同学错把c写成了几?21世纪教育网版权所有
8.阅读下面解方程组的方法,然后解答问题.
解方程组
解:①-②,得2x+2y=2,即x+y=1.③
③×16,得16x+16y=16.④
②-④,得x=-1.把x=-1代入③,得y=2.
所以原方程组的解是
(1)请你仿照上面的解法解方程组
(2)请大胆猜测关于x,y的方程组
(a≠b)的解.
参考答案
【基础训练】
1.【答案】D 2.【答案】B 3.【答案】A
4.【答案】4
解:由题意可得方程组
①×2得:2x-4y-2=0③,③-②得-3y+3=0,解得y=1,代入①解得:x=3.所以原方程组的解为所以x+y=4.
5.解:(1)①+②得:3x=15,所以x=5.
将x=5代入①,得:5+y=6,所以y=1,所以方程组的解为
(2)②×3,得3x+9y=21,③
③-①,得11y=22.所以y=2.
把y=2代入②,得x+6=7,所以x=1,所以原方程组的解为
(3)①×3+②,得10x=20,解得x=2.
把x=2代入①,得6-y=7,解得y=-1.所以原方程组的解为
分析:解二元一次方程组的基本思想是消元,基本方法有代入法和加减法. 当其中一个未知数的系数是1或-1时,用代入法简单;当同一未知数的系数相等、互为相反数或绝对值成整数关系时,用加减法简单.
【培优提升】
1.【答案】D 2.【答案】A
3.【答案】A
解:由题意得方程组
解得所以=.
4.【答案】4
解:本题运用整体思想解答.把x+y看成一个整体,可使问题简单化. ①+②,得4x+4y=a+4,x+y=.又因为x+y=2,所以=2,解得a=4.21教育网
5.解:(1)由②得:x-y=,③
①-③得:x=.
将x=代入③得:y=4.
所以这个方程组的解是
(2)①×36得,12x+9y=72 ③,②×48得,12x+16y=96 ④,④-③,得7y=24,解得y=.将y=代入①,解得x=.所以原方程组的解为21cnjy.com
6.解:解方程组得将其代入ax+by=-1,2ax+3by=3,可得①×2-②,得-b=-5,所以b=5.把b=5代入①,得a=-2.所以a,b的值分别为-2,5.21·cn·jy·com
分析:既然两个方程组的解相同,那么两个方程组的解也应与方程组的解相同,将此方程组的解代入含有a,b的两个方程中,得到关于a,b的二元一次方程组,从而求出a,b的值.
7.解:由题意,得设乙同学错把c写为c',则
所以解得a=4.
把a=4分别代入①,②,得6-2c=2×4,-4+2c'=2×4,所以c=-1,c'=6.所以c的值为-1,乙同学错把c写成了6.www.21-cn-jy.com
8.解:(1)①-②,得2x+2y=2,即x+y=1③.③×2 014,得2 014x+2 014y=2 014④.②-④,得x=-1.把x=-1代入③,得y=2.所以原方程组的解是2·1·c·n·j·y
(2)
分析:观察例题中方程组的特点找出规律,利用此规律解方程组.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
