11.1三角形的有关线段复习课件
图片预览


文档简介
课件31张PPT。知识点1. 三角形的概念
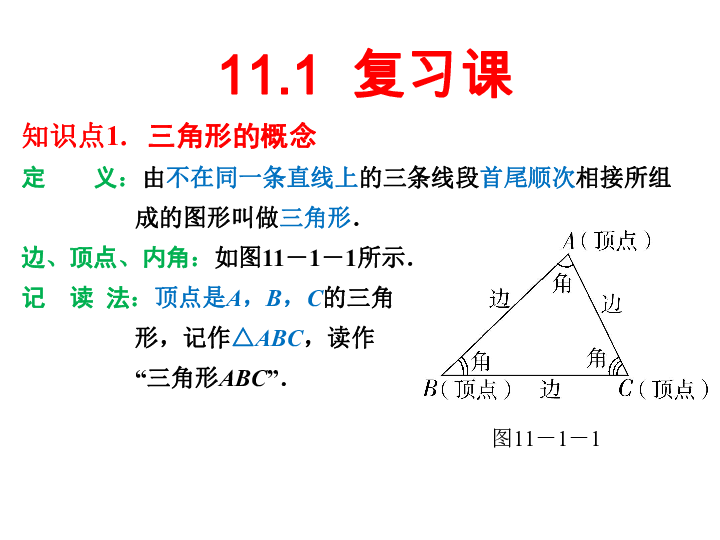
定 义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
边、顶点、内角:如图11-1-1所示.
记 读 法:顶点是A,B,C的三角
形,记作△ABC,读作
“三角形ABC”.
11.1 复习课 图11-1-1知识点2.三角形的三边关系
性 质:三角形两边的和________第三边.
说 明:三角形两边的差________第三边.
注 意:通过三角形三边关系可判断三条线段能否构成三角形.
知识点3.等腰三角形
定 义:有两边相等的三角形叫做等腰三角形;
三边相等的三角形叫做等边三角形.
腰、底:在等腰三角形中,相等的两边叫做腰,另一边叫做底.
顶 角:两腰的夹角叫做顶角.
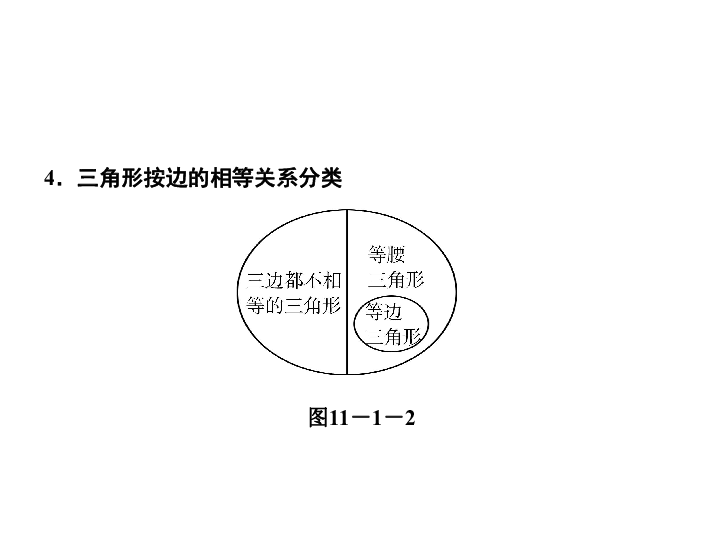
底 角:腰和底边的夹角叫做底角.大于小于4.三角形按边的相等关系分类
图11-1-2 类型之一 三角形的概念
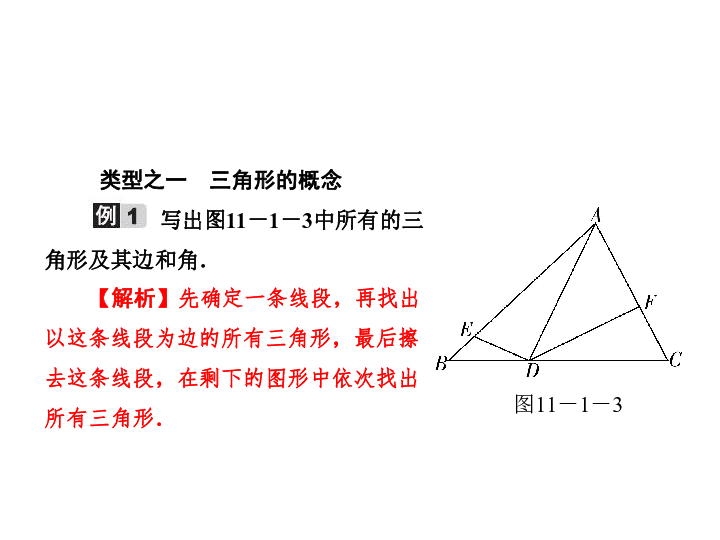
写出图11-1-3中所有的三
角形及其边和角.
图11-1-3【解析】先确定一条线段,再找出以这条线段为边的所有三角形,最后擦去这条线段,在剩下的图形中依次找出所有三角形.解:△ADE,边为AD,DE,EA,角为∠ADE,∠DEA,∠EAD;
△ADB,边为AD,DB,BA,角为∠ADB,∠DBA,∠BAD;
△ADF,边为AD,DF,FA,角为∠ADF,∠DFA,∠FAD;
△ADC,边为AD,DC,CA,角为∠ADC,∠DCA,∠CAD;
△DEB,边为DE,EB,BD,角为∠DEB,∠EBD,∠BDE;
△DFC,边为DF,FC,CD,角为∠DFC,∠FCD,∠CDF;
△ABC,边为AB,BC,CA,角为∠ABC,∠BCA,∠CAB.
【点悟】 找三角形时应按一定的规律,以边为线索找三角形或以角为线索找三角形,体现了分类讨论思想.类型之二 三角形的三边关系
已知三角形的两边长分别为3和6,第三边长是奇数,则第三边长可以是 ( )
A.1 B.3 C.5 D.9
【解析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围;又知道第三边长为奇数,就可以得出第三边的长度.
设第三边的长为x,根据三角形的三边关系,
得6-3又∵第三边长是奇数,
∴x=5或7.C
【点悟】 求三角形第三边的范围的问题就是根据三角形三边关系列出不等式组,然后解不等式组.1.[2014·西宁]下列线段能构成三角形的是 ( )
A.2,2,4 B.3,4,5
C.1,2,3 D.2,3,6
2.[2014·宜昌]已知三角形两边长分别为3和8,则该三角形第三边的长可能是 ( )
A.5 B.10
C.11 D.12
【解析】三角形两边之和大于第三边,两边之差小于第三边.BB3.如图11-1-4,图中三角形的个数共有 ( )
图11-1-4
A.1个 B.2个
C.3个 D.4个
【解析】图中三角形有△ABD,△ADC,△ABC.
C4.[2014·淮安]若一个三角形三边长分别为2,3,x,则x的值可以为_________________.(只需填一个数)2(答案不唯一)1.三角形的高、中线与角平分线的概念
高 :从三角形的一个顶点向它所对的边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高.
中 线:在三角形中,连接一个顶点和它所对的边的中点的线段叫做三角形的中线.
角平分线:在三角形中,一个内角的平分线和它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
注 意:三角形的高、中线与角平分线均指________,而垂线是________,角平分线是________.线段直线射线2.三角形的重心及面积公式
重 心:三角形三条中线的交点叫做三角形的重心.
规 律:三角形一边上的中线把三角形面积两等分.类型之一 三角形的高、中线与角平分线的概念
图11-1-9 如图11-1-9所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,给出下列判断:①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高.其中正确的个数是 ( )
B A.0 B.1 C.2 D.3【解析】由∠1=∠2得AD平分∠BAE,但AD不是△ABE内的线段,所以①不正确;同样BE虽然经过边AD的中点G,但BE也不是△ABD内的线段,所以②也不正确;由于CH⊥AD于H,所以CH是△ACD的边AD上的高,所以③是正确的,即三个判断中只有一个正确.故选B.
【点悟】 三角形的角平分线、中线、高是三条重要的线段,掌握它们的概念是关键.类型之二 三角形的面积
如图11-1-10所示,已知AD,AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
图11-1-10【点悟】 (1)利用面积关系求直角三角形斜边上的高;(2)三角形一边上的中线把三角形的面积两等分.1.小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是
( )C2.不一定在三角形内部的线段是 ( )
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.以上答案均不正确3.如图11-1-11,图中共有______个三角形,若BC=CD=DE,则AC,AD分别是__________,__________的中线.
【解析】图中共有6个三角形,它们分别是△ABC,△ACD,△ADE,△ABD,△ACE,△ABE.因为BC=CD,所以AC是△ABD的中线;因为CD=DE,所以AD是△ACE的中线.
图11-1-11C6△ABD△ACE4.如图11-1-12,AD、AM、AH分别是△ABC的角平分线、中线和高.图11-1-12BADCADBAC(3)因为AH是△ABC的高,所以∠_________=∠________=90°.BMCMBCAHBAHC1.三角形的稳定性
规 律:三角形具有________性,而四边形具有_________性.
2.判定多边形是否具有稳定性
方 法:因为三角形具有稳定性,所以多边形只要可以分解成三角形,就有稳定性.稳定不稳定
在建筑工地我们常看见如图11-1-20所示,用木条EF固定矩形门框ABCD的情形,这种做法是根据 ( )
A.两点之间线段最短
B.两点确定一条直线
C.三角形的稳定性
D.矩形的四个角是直角
类型之一 三角形的稳定性及四边形的不稳定性的应用图11-1-20C【点悟】 考查三角形具有稳定性这一知识点,类似的利用三角形具有稳定性原理的例子还有桥梁、自行车、横梁等. 如图11-1-21是一个活动挂衣架,你能说明制作这个活动挂衣架的依据吗?你知道如何使用这个挂衣架吗?
解:四边形具有不稳定性.不用时,把衣架两端往中间挤,以便收起,使用时,可以把衣架朝两边拉开.图11-1-21类型之二 判断图形是否具有稳定性
(1)如图11-1-22所示的图形中,哪些具有稳定性?图11-1-22(2)对不具有稳定性的图形,请适当的添加线段,使之具有稳定性.
【解析】(1)根据“三角形具有稳定性,而四边形不具有稳定性”可作出判断;(2)添加后须构成三角形.
解:(1)具有稳定性的图形是(1)(4)(6).
(2)答案不唯一,如图所示.
例3答图【点悟】 (1)三角形具有稳定性,而四边形不具有稳定性;(2)对不具有稳定性的图形,添加线段后构成三角形,使之具有稳定性.1.下列图形中具有稳定性的是 ( )
A.正方形 B.长方形
C.梯形 D.直角三角形
2.下列图形中具有稳定性的是 ( )DD3.用小木条钉成一个三角形木架和一个四边形木架,分别扭动它们就会发现,三角形木架的形状不会发生改变,这是因为____ ________________,而四边形木架的形状会发生改变,这是因为______________________.三角形具有稳定性四边形具有不稳定性
4.空调安装在墙上时,一般都会像如图11-1-23所示的方法固定在墙上,这种方法应用的数学知识是__________________.
图11-1-23三角形的稳定性
定 义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
边、顶点、内角:如图11-1-1所示.
记 读 法:顶点是A,B,C的三角
形,记作△ABC,读作
“三角形ABC”.
11.1 复习课 图11-1-1知识点2.三角形的三边关系
性 质:三角形两边的和________第三边.
说 明:三角形两边的差________第三边.
注 意:通过三角形三边关系可判断三条线段能否构成三角形.
知识点3.等腰三角形
定 义:有两边相等的三角形叫做等腰三角形;
三边相等的三角形叫做等边三角形.
腰、底:在等腰三角形中,相等的两边叫做腰,另一边叫做底.
顶 角:两腰的夹角叫做顶角.
底 角:腰和底边的夹角叫做底角.大于小于4.三角形按边的相等关系分类
图11-1-2 类型之一 三角形的概念
写出图11-1-3中所有的三
角形及其边和角.
图11-1-3【解析】先确定一条线段,再找出以这条线段为边的所有三角形,最后擦去这条线段,在剩下的图形中依次找出所有三角形.解:△ADE,边为AD,DE,EA,角为∠ADE,∠DEA,∠EAD;
△ADB,边为AD,DB,BA,角为∠ADB,∠DBA,∠BAD;
△ADF,边为AD,DF,FA,角为∠ADF,∠DFA,∠FAD;
△ADC,边为AD,DC,CA,角为∠ADC,∠DCA,∠CAD;
△DEB,边为DE,EB,BD,角为∠DEB,∠EBD,∠BDE;
△DFC,边为DF,FC,CD,角为∠DFC,∠FCD,∠CDF;
△ABC,边为AB,BC,CA,角为∠ABC,∠BCA,∠CAB.
【点悟】 找三角形时应按一定的规律,以边为线索找三角形或以角为线索找三角形,体现了分类讨论思想.类型之二 三角形的三边关系
已知三角形的两边长分别为3和6,第三边长是奇数,则第三边长可以是 ( )
A.1 B.3 C.5 D.9
【解析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围;又知道第三边长为奇数,就可以得出第三边的长度.
设第三边的长为x,根据三角形的三边关系,
得6-3
∴x=5或7.C
【点悟】 求三角形第三边的范围的问题就是根据三角形三边关系列出不等式组,然后解不等式组.1.[2014·西宁]下列线段能构成三角形的是 ( )
A.2,2,4 B.3,4,5
C.1,2,3 D.2,3,6
2.[2014·宜昌]已知三角形两边长分别为3和8,则该三角形第三边的长可能是 ( )
A.5 B.10
C.11 D.12
【解析】三角形两边之和大于第三边,两边之差小于第三边.BB3.如图11-1-4,图中三角形的个数共有 ( )
图11-1-4
A.1个 B.2个
C.3个 D.4个
【解析】图中三角形有△ABD,△ADC,△ABC.
C4.[2014·淮安]若一个三角形三边长分别为2,3,x,则x的值可以为_________________.(只需填一个数)2(答案不唯一)1.三角形的高、中线与角平分线的概念
高 :从三角形的一个顶点向它所对的边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高.
中 线:在三角形中,连接一个顶点和它所对的边的中点的线段叫做三角形的中线.
角平分线:在三角形中,一个内角的平分线和它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
注 意:三角形的高、中线与角平分线均指________,而垂线是________,角平分线是________.线段直线射线2.三角形的重心及面积公式
重 心:三角形三条中线的交点叫做三角形的重心.
规 律:三角形一边上的中线把三角形面积两等分.类型之一 三角形的高、中线与角平分线的概念
图11-1-9 如图11-1-9所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,给出下列判断:①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高.其中正确的个数是 ( )
B A.0 B.1 C.2 D.3【解析】由∠1=∠2得AD平分∠BAE,但AD不是△ABE内的线段,所以①不正确;同样BE虽然经过边AD的中点G,但BE也不是△ABD内的线段,所以②也不正确;由于CH⊥AD于H,所以CH是△ACD的边AD上的高,所以③是正确的,即三个判断中只有一个正确.故选B.
【点悟】 三角形的角平分线、中线、高是三条重要的线段,掌握它们的概念是关键.类型之二 三角形的面积
如图11-1-10所示,已知AD,AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
图11-1-10【点悟】 (1)利用面积关系求直角三角形斜边上的高;(2)三角形一边上的中线把三角形的面积两等分.1.小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是
( )C2.不一定在三角形内部的线段是 ( )
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.以上答案均不正确3.如图11-1-11,图中共有______个三角形,若BC=CD=DE,则AC,AD分别是__________,__________的中线.
【解析】图中共有6个三角形,它们分别是△ABC,△ACD,△ADE,△ABD,△ACE,△ABE.因为BC=CD,所以AC是△ABD的中线;因为CD=DE,所以AD是△ACE的中线.
图11-1-11C6△ABD△ACE4.如图11-1-12,AD、AM、AH分别是△ABC的角平分线、中线和高.图11-1-12BADCADBAC(3)因为AH是△ABC的高,所以∠_________=∠________=90°.BMCMBCAHBAHC1.三角形的稳定性
规 律:三角形具有________性,而四边形具有_________性.
2.判定多边形是否具有稳定性
方 法:因为三角形具有稳定性,所以多边形只要可以分解成三角形,就有稳定性.稳定不稳定
在建筑工地我们常看见如图11-1-20所示,用木条EF固定矩形门框ABCD的情形,这种做法是根据 ( )
A.两点之间线段最短
B.两点确定一条直线
C.三角形的稳定性
D.矩形的四个角是直角
类型之一 三角形的稳定性及四边形的不稳定性的应用图11-1-20C【点悟】 考查三角形具有稳定性这一知识点,类似的利用三角形具有稳定性原理的例子还有桥梁、自行车、横梁等. 如图11-1-21是一个活动挂衣架,你能说明制作这个活动挂衣架的依据吗?你知道如何使用这个挂衣架吗?
解:四边形具有不稳定性.不用时,把衣架两端往中间挤,以便收起,使用时,可以把衣架朝两边拉开.图11-1-21类型之二 判断图形是否具有稳定性
(1)如图11-1-22所示的图形中,哪些具有稳定性?图11-1-22(2)对不具有稳定性的图形,请适当的添加线段,使之具有稳定性.
【解析】(1)根据“三角形具有稳定性,而四边形不具有稳定性”可作出判断;(2)添加后须构成三角形.
解:(1)具有稳定性的图形是(1)(4)(6).
(2)答案不唯一,如图所示.
例3答图【点悟】 (1)三角形具有稳定性,而四边形不具有稳定性;(2)对不具有稳定性的图形,添加线段后构成三角形,使之具有稳定性.1.下列图形中具有稳定性的是 ( )
A.正方形 B.长方形
C.梯形 D.直角三角形
2.下列图形中具有稳定性的是 ( )DD3.用小木条钉成一个三角形木架和一个四边形木架,分别扭动它们就会发现,三角形木架的形状不会发生改变,这是因为____ ________________,而四边形木架的形状会发生改变,这是因为______________________.三角形具有稳定性四边形具有不稳定性
4.空调安装在墙上时,一般都会像如图11-1-23所示的方法固定在墙上,这种方法应用的数学知识是__________________.
图11-1-23三角形的稳定性
