8.4.2 单项式与多项式相乘 同步练习
文档属性
| 名称 | 8.4.2 单项式与多项式相乘 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 365.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-24 09:07:41 | ||
图片预览
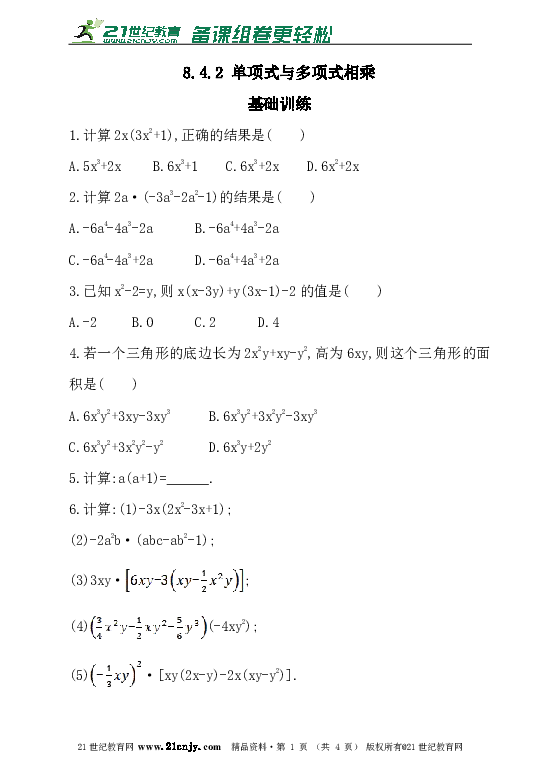


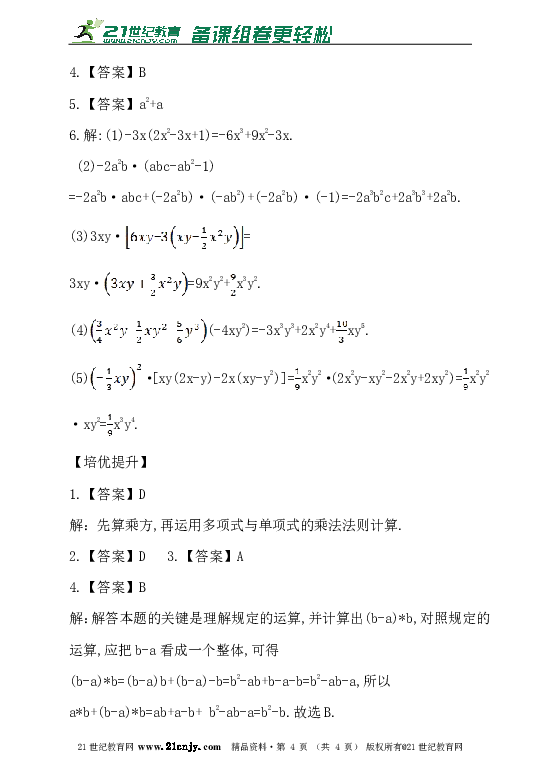
文档简介
8.4.2 单项式与多项式相乘
基础训练
1.计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1 C.6x3+2x D.6x2+2x
2.计算2a·(-3a3-2a2-1)的结果是( )
A.-6a4-4a3-2a B.-6a4+4a3-2a
C.-6a4-4a3+2a D.-6a4+4a3+2a
3.已知x2-2=y,则x(x-3y)+y(3x-1)-2的值是( )
A.-2 B.0 C.2 D.4
4.若一个三角形的底边长为2x2y+xy-y2,高为6xy,则这个三角形的面积是( )
A.6x3y2+3xy-3xy3 B.6x3y2+3x2y2-3xy3
C.6x3y2+3x2y2-y2 D.6x3y+2y2
5.计算:a(a+1)=______.
6.计算:(1)-3x(2x2-3x+1);
(2)-2a2b·(abc-ab2-1);
(3)3xy·;
(4)(-4xy2);
(5)·[xy(2x-y)-2x(xy-y2)].
培优提升
1.(-3x+1)(-2x)2等于( )
A.-6x3-2x2 B.6x3-2x2 C.6x3+2x2 D.-12x3+4x2
2.当a=4,b=2,c=时,a(b-c)-b(c-a)+c(a-b)的值为( )
A.5 B.10 C.12 D.14
3.下列计算正确的是( )
A.xn(xn-x2+3)=x2n-xn+2+3xn
B.(2x+3y)(-4xy)=-8x2y-12xy2=-20xy
C.(-2xy2-4x2y)(-3xyz)=6x2y3+12x3y2
D.(xyz-7x2y+1)(-xz)=-x2yz2+7x3yz
4.现规定一种运算:a*b=ab+a-b,其中a,b为有理数,则a*b+(b-a)*b等于( )
A.a2-b B.b2-b C.b2 D.b2-a
5.若-2x2y(-xmy+3xy3)=2x5y2-6x3yn,则m=__________,n= .?
6.计算下列各题:
(1);
(2)2ab(a2b2-ab+1)+3ab(1-ab).
7.先化简,再求值:3(2x+1)+2(3-x),其中x=-1.
8.已知ab2=-1,求(-ab)(a2b5-ab3-b)的值.
9.已知-2m2(3m2-pm-6)-3m3+m2中不含m3项,试确定p的值.
10.一张长方形硬纸片,长为(5a2+4b2)m,宽为6a4 m,若在它的四个角上分别剪去一个边长为a3 m的小正方形,然后折叠成一个无盖的盒子,求这个无盖的盒子的表面积.21cnjy.com
参考答案
【基础训练】
1.【答案】C 2.【答案】A
3.【答案】B
解:x(x-3y)+y(3x-1)-2化简后的结果是x2-y-2,由x2-2=y可得x2-y-2=0.21·cn·jy·com
4.【答案】B
5.【答案】a2+a
6.解:(1)-3x(2x2-3x+1)=-6x3+9x2-3x.
(2)-2a2b·(abc-ab2-1)
=-2a2b·abc+(-2a2b)·(-ab2)+(-2a2b)·(-1)=-2a3b2c+2a3b3+2a2b.
(3)3xy·=
3xy·=9x2y2+x3y2.
(4)(-4xy2)=-3x3y3+2x2y4+xy5.
(5)·[xy(2x-y)-2x(xy-y2)]=x2y2·(2x2y-xy2-2x2y+2xy2)=x2y2·xy2=x3y4.【来源:21·世纪·教育·网】
【培优提升】
1.【答案】D
解:先算乘方,再运用多项式与单项式的乘法法则计算.
2.【答案】D 3.【答案】A
4.【答案】B
解:解答本题的关键是理解规定的运算,并计算出(b-a)*b,对照规定的运算,应把b-a看成一个整体,可得21世纪教育网版权所有
(b-a)*b=(b-a)b+(b-a)-b=b2-ab+b-a-b=b2-ab-a,所以
a*b+(b-a)*b=ab+a-b+ b2-ab-a=b2-b.故选B.
5.【答案】3;4
解:∵-2x2y(-xmy+3xy3)=2xm+2y2-6x3y4=2x5y2-6x3yn,
∴m+2=5,n=4,∴m=3,n=4.
6.解:(1)原式
=x2y2·=x2y2·x2y-x2y2·8xy2+x2y2·5x-x2y2=x4y3-2x3y4+x3y2-x2y2; 2·1·c·n·j·y
(2)原式
=2ab·a2b2-2ab·ab+2ab+3ab-3ab·ab=2a3b3-2a2b2+5ab-3a2b2=2a3b3-5a2b2+5ab.21教育网
7.解:原式=6x+3+6-2x
=4x+9.
当x=-1时,原式=4×(-1)+9=5.
8.解:原式=-a3b6+a2b4+ab2=-(ab2)3+(ab2)2+ab2=-(-1)3+(-1)2+(-1)=1.
9.解:-2m2(3m2-pm-6)-3m3+m2=-6m4+2pm3+12m2-3m3+m2=-6m4+(2p-3)m3+13m2,由题意可知2p-3=0,∴p=.www.21-cn-jy.com
10.解:这个无盖的盒子的表面积为:
6a4(5a2+4b2)-4×
=6a4(5a2+4b2)-4×a6
=30a6+24a4b2-9a6
=(21a6+24a4b2)(m2).
答:这个无盖的盒子的表面积为(21a6+24a4b2)m2.
基础训练
1.计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1 C.6x3+2x D.6x2+2x
2.计算2a·(-3a3-2a2-1)的结果是( )
A.-6a4-4a3-2a B.-6a4+4a3-2a
C.-6a4-4a3+2a D.-6a4+4a3+2a
3.已知x2-2=y,则x(x-3y)+y(3x-1)-2的值是( )
A.-2 B.0 C.2 D.4
4.若一个三角形的底边长为2x2y+xy-y2,高为6xy,则这个三角形的面积是( )
A.6x3y2+3xy-3xy3 B.6x3y2+3x2y2-3xy3
C.6x3y2+3x2y2-y2 D.6x3y+2y2
5.计算:a(a+1)=______.
6.计算:(1)-3x(2x2-3x+1);
(2)-2a2b·(abc-ab2-1);
(3)3xy·;
(4)(-4xy2);
(5)·[xy(2x-y)-2x(xy-y2)].
培优提升
1.(-3x+1)(-2x)2等于( )
A.-6x3-2x2 B.6x3-2x2 C.6x3+2x2 D.-12x3+4x2
2.当a=4,b=2,c=时,a(b-c)-b(c-a)+c(a-b)的值为( )
A.5 B.10 C.12 D.14
3.下列计算正确的是( )
A.xn(xn-x2+3)=x2n-xn+2+3xn
B.(2x+3y)(-4xy)=-8x2y-12xy2=-20xy
C.(-2xy2-4x2y)(-3xyz)=6x2y3+12x3y2
D.(xyz-7x2y+1)(-xz)=-x2yz2+7x3yz
4.现规定一种运算:a*b=ab+a-b,其中a,b为有理数,则a*b+(b-a)*b等于( )
A.a2-b B.b2-b C.b2 D.b2-a
5.若-2x2y(-xmy+3xy3)=2x5y2-6x3yn,则m=__________,n= .?
6.计算下列各题:
(1);
(2)2ab(a2b2-ab+1)+3ab(1-ab).
7.先化简,再求值:3(2x+1)+2(3-x),其中x=-1.
8.已知ab2=-1,求(-ab)(a2b5-ab3-b)的值.
9.已知-2m2(3m2-pm-6)-3m3+m2中不含m3项,试确定p的值.
10.一张长方形硬纸片,长为(5a2+4b2)m,宽为6a4 m,若在它的四个角上分别剪去一个边长为a3 m的小正方形,然后折叠成一个无盖的盒子,求这个无盖的盒子的表面积.21cnjy.com
参考答案
【基础训练】
1.【答案】C 2.【答案】A
3.【答案】B
解:x(x-3y)+y(3x-1)-2化简后的结果是x2-y-2,由x2-2=y可得x2-y-2=0.21·cn·jy·com
4.【答案】B
5.【答案】a2+a
6.解:(1)-3x(2x2-3x+1)=-6x3+9x2-3x.
(2)-2a2b·(abc-ab2-1)
=-2a2b·abc+(-2a2b)·(-ab2)+(-2a2b)·(-1)=-2a3b2c+2a3b3+2a2b.
(3)3xy·=
3xy·=9x2y2+x3y2.
(4)(-4xy2)=-3x3y3+2x2y4+xy5.
(5)·[xy(2x-y)-2x(xy-y2)]=x2y2·(2x2y-xy2-2x2y+2xy2)=x2y2·xy2=x3y4.【来源:21·世纪·教育·网】
【培优提升】
1.【答案】D
解:先算乘方,再运用多项式与单项式的乘法法则计算.
2.【答案】D 3.【答案】A
4.【答案】B
解:解答本题的关键是理解规定的运算,并计算出(b-a)*b,对照规定的运算,应把b-a看成一个整体,可得21世纪教育网版权所有
(b-a)*b=(b-a)b+(b-a)-b=b2-ab+b-a-b=b2-ab-a,所以
a*b+(b-a)*b=ab+a-b+ b2-ab-a=b2-b.故选B.
5.【答案】3;4
解:∵-2x2y(-xmy+3xy3)=2xm+2y2-6x3y4=2x5y2-6x3yn,
∴m+2=5,n=4,∴m=3,n=4.
6.解:(1)原式
=x2y2·=x2y2·x2y-x2y2·8xy2+x2y2·5x-x2y2=x4y3-2x3y4+x3y2-x2y2; 2·1·c·n·j·y
(2)原式
=2ab·a2b2-2ab·ab+2ab+3ab-3ab·ab=2a3b3-2a2b2+5ab-3a2b2=2a3b3-5a2b2+5ab.21教育网
7.解:原式=6x+3+6-2x
=4x+9.
当x=-1时,原式=4×(-1)+9=5.
8.解:原式=-a3b6+a2b4+ab2=-(ab2)3+(ab2)2+ab2=-(-1)3+(-1)2+(-1)=1.
9.解:-2m2(3m2-pm-6)-3m3+m2=-6m4+2pm3+12m2-3m3+m2=-6m4+(2p-3)m3+13m2,由题意可知2p-3=0,∴p=.www.21-cn-jy.com
10.解:这个无盖的盒子的表面积为:
6a4(5a2+4b2)-4×
=6a4(5a2+4b2)-4×a6
=30a6+24a4b2-9a6
=(21a6+24a4b2)(m2).
答:这个无盖的盒子的表面积为(21a6+24a4b2)m2.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
