9.2.1 三角形的内角 同步练习

9.2.1 三角形的内角
基础训练
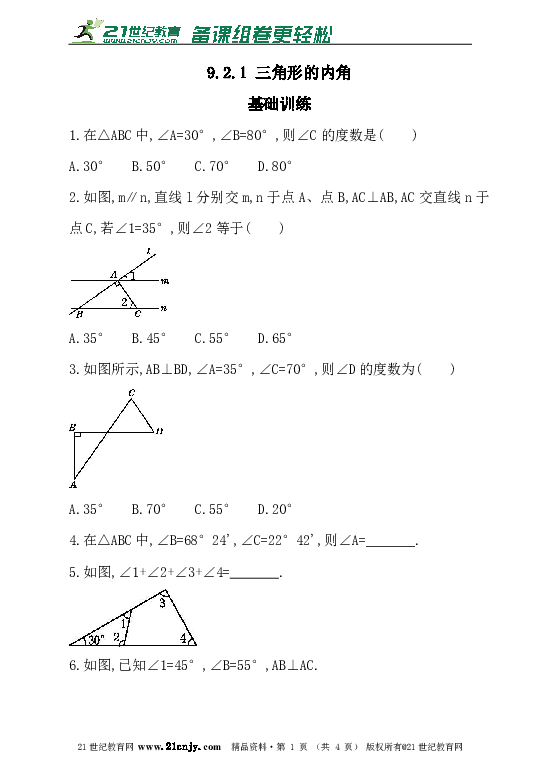
1.在△ABC中,∠A=30°,∠B=80°,则∠C的度数是(　　)
A.30° B.50° C.70° D.80°
2.如图,m∥n,直线l分别交m,n于点A、点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于(　　)21cnjy.com
A.35° B.45° C.55° D.65°
3.如图所示,AB⊥BD,∠A=35°,∠C=70°,则∠D的度数为(　　)
A.35° B.70° C.55° D.20°
4.在△ABC中,∠B=68°24',∠C=22°42',则∠A=_______.
5.如图,∠1+∠2+∠3+∠4=_______.
6.如图,已知∠1=45°,∠B=55°,AB⊥AC.
(1)求∠ACB的度数;
(2)AD与BC平行吗?为什么?
　 　　
培优提升
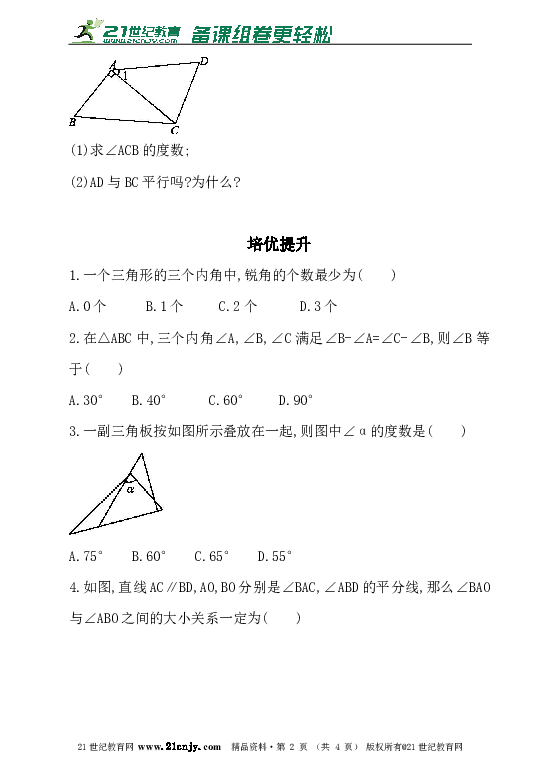
1.一个三角形的三个内角中,锐角的个数最少为(　　)
A.0个 B.1个 C.2个 D.3个
2.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B等于(　　)
A.30° B.40° C.60° D.90°
3.一副三角板按如图所示叠放在一起,则图中∠α的度数是(　　)
A.75° B.60° C.65° D.55°
4.如图,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么∠BAO与∠ABO之间的大小关系一定为(　　)21世纪教育网版权所有
A.互余 　　　B.相等 C.互补 　　　D.不等
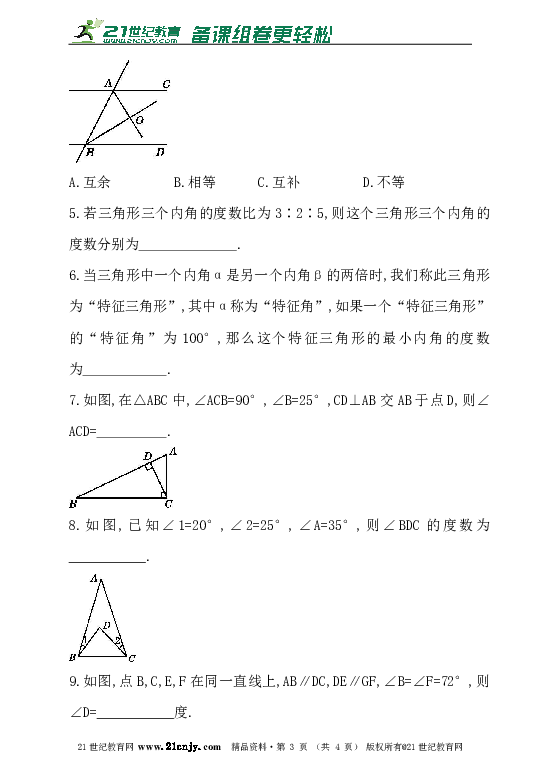
5.若三角形三个内角的度数比为3∶2∶5,则这个三角形三个内角的度数分别为　　　　　　　.
6.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”,如果一个“特征三角形”的“特征角”为100°,那么这个特征三角形的最小内角的度数为　　　　　　.www.21-cn-jy.com
7.如图,在△ABC中,∠ACB=90°,∠B=25°,CD⊥AB交AB于点D,则∠ACD=　　　　　.?2·1·c·n·j·y
8.如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为___________.
9.如图,点B,C,E,F在同一直线上,AB∥DC,DE∥GF,∠B=∠F=72°,则∠D=___________度.21·cn·jy·com
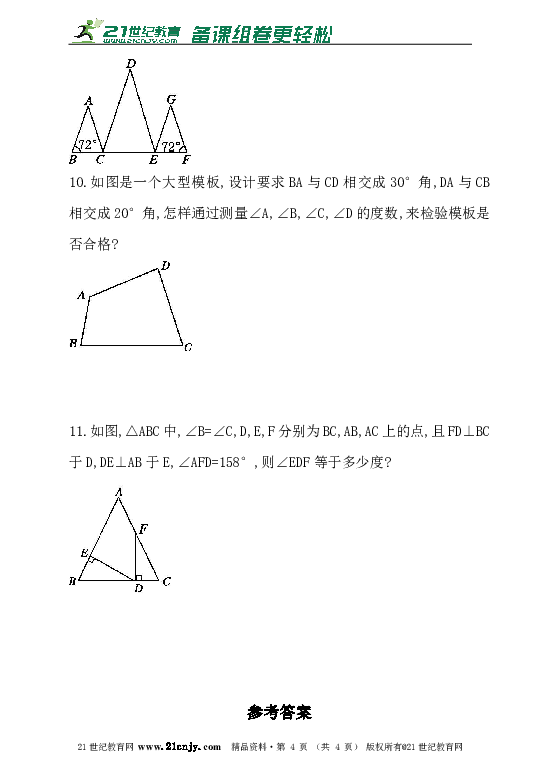
10.如图是一个大型模板,设计要求BA与CD相交成30°角,DA与CB相交成20°角,怎样通过测量∠A,∠B,∠C,∠D的度数,来检验模板是否合格?【来源：21·世纪·教育·网】
11.如图,△ABC中,∠B=∠C,D,E,F分别为BC,AB,AC上的点,且FD⊥BC于D,DE⊥AB于E,∠AFD=158°,则∠EDF等于多少度?
参考答案
【基础训练】
1.【答案】C
解：由三角形内角和为180°可知:∠A+∠B+∠C=180°,所以∠
C=180°-∠A-∠B=180°-30°-80°=70°.
2.【答案】C
3.【答案】C
4.【答案】88°54'
解：根据三角形内角和是180°,可得∠A=180°-(∠B+∠C)=180°-(68°24'+22°42')=180°-91°6'=88°54'.
5.【答案】300°
解：由三角形内角和定理可得出∠1+∠2=∠3+∠4=150°,从而可确定4个角的和.
6.解:(1)因为∠B=55°,AB⊥AC,即∠BAC=90°,所以∠ACB=90°-∠
B=35°.
(2)AD与BC不平行.理由:由(1)知,∠ACB=35°,而∠1=45°,∠1≠∠ACB,所以AD与BC不平行.21教育网
【培优提升】
1.【答案】C
解：本题运用转化思想.问题可转化为一个三角形的三个内角中,钝角或直角的个数最多为几个.
2.【答案】C
解：本题运用方程思想和整体思想.由∠B-∠A=∠C-∠B,得2∠B=∠A+∠C.根据三角形内角和是180°,可得∠A+∠B+∠C=180°,将∠A+∠C=2∠B整体代入,得∠B+2∠B=180°,解得∠B=60°.
3.【答案】A
解：根据三角形内角和定理与三角板中角的度数可得∠α=180°-45°-60°=75°.
4.【答案】A
5.【答案】54°、36°、90°
解：本题运用方程思想.设三角形的三个内角的度数分别为3x、2x、5x,由三角形的内角和定理可得3x+2x+5x=180°,解得x=18°.故
3x=54°,2x=36°,5x=90°.
6.【答案】30°
解：本题关键在于将“特征角”的定义理解透彻.即当α=100°时,β=α=50°,再根据三角形内角和求得另一个角为
180°-100°-50°=30°,即最小内角度数为30°.
7.【答案】25°　 8.【答案】80°
9.【答案】36
解：根据两直线平行,同位角相等可得∠DCE=∠B=72°,∠DEC=∠
F=72°,再利用三角形内角和定理,得∠D=180°-∠DCE-∠
DEC=180°-72°-72°=36°.
10.解:如图,延长DA,CB交于点F,延长CD,BA交于点E.测量∠ABC,∠C,∠CDA的度数,若180°-(∠ABC+∠C)=30°与180°-(∠C+∠
CDA)=20°同时成立,则模板合格;否则不合格.
11.解:∵∠AFD=158°,∴∠CFD=180°-158°=22°.
∵DF⊥BC,
∴∠BDF=∠CDF=90°.∴在Rt△CDF中,∠C=90°-∠
CFD=90°-22°=68°.又∵∠B=∠C,∴∠B=68°.∵DE⊥AB,∴∠
BED=90°.
∴在Rt△BDE中,∠BDE=90°-∠B=90°-68°=22°.
∴∠EDF=∠BDF-∠BDE=90°-22°=68°.