9.2.2 三角形的外角 同步练习

9.2.2 三角形的外角
基础训练
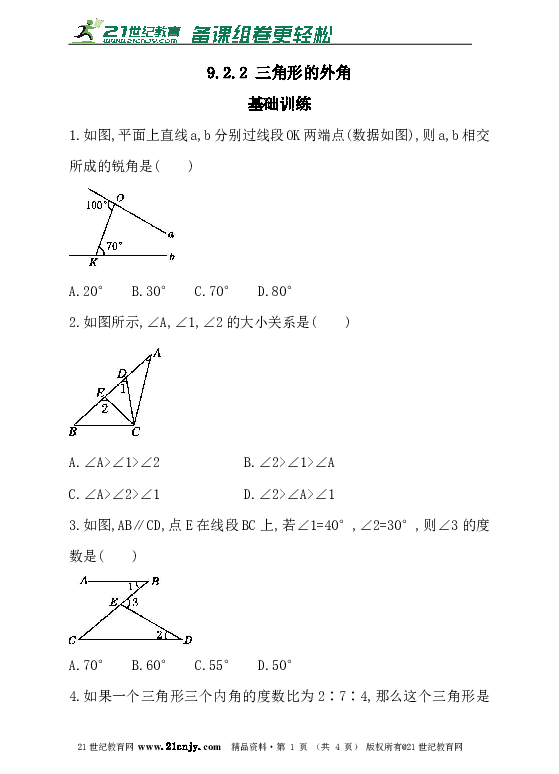
1.如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是(　　)
A.20° B.30° C.70° D.80°
2.如图所示,∠A,∠1,∠2的大小关系是(　　)
A.∠A>∠1>∠2 B.∠2>∠1>∠A
C.∠A>∠2>∠1 D.∠2>∠A>∠1
3.如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是(　　)
A.70° B.60° C.55° D.50°
4.如果一个三角形三个内角的度数比为2∶7∶4,那么这个三角形是(　　)
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
5.如图是一副三角板叠放的示意图,则∠α=　　　　　.
6.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
培优提升
1.如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为(　　)21·cn·jy·com
A.30° B.60° C.90° D.120°
2.如图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上,如果∠2=60°,那么∠1的度数为(　　)
A.60° B.50° C.40° D.30°
3.如图,把一直尺放置在一个三角形纸片上,则下列结论正确的是(　　)
A.∠1+∠6>180° B.∠2+∠5<180°
C.∠3+∠4<180° D.∠3+∠7>180°
4.如图,在△ABC中,外角∠EBC和外角∠FCB的平分线交于点D,设∠BDC=m, 则∠A=(　　)【来源：21·世纪·教育·网】
A.90°-m B.90°-
C.180°-2m D.180°-
5.下列条件中,能判断△ABC是直角三角形的条件有_____.(填序号)
①∠A+∠B=∠C; ②∠A∶∠B∶∠C=1∶2∶3;
③∠A=90°-∠B;④∠A=∠B=∠C;⑤∠A=2∠B=3∠C.
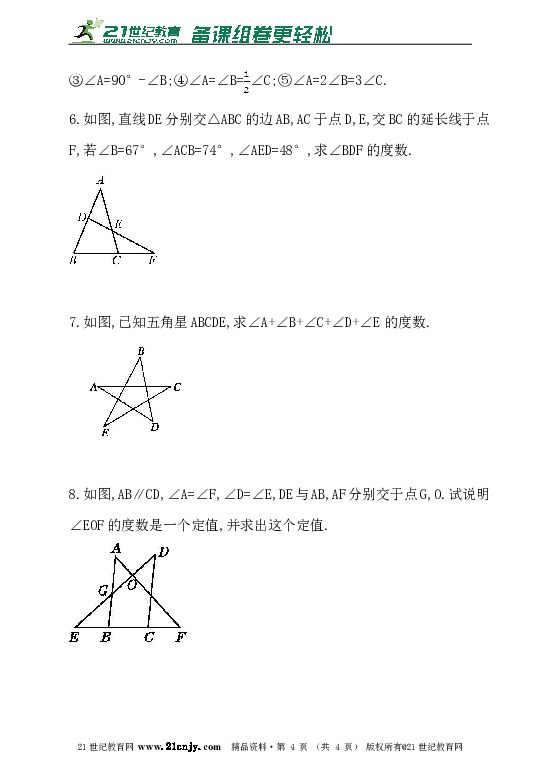
6.如图,直线DE分别交△ABC的边AB,AC于点D,E,交BC的延长线于点F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.
7.如图,已知五角星ABCDE,求∠A+∠B+∠C+∠D+∠E的度数.

8.如图,AB∥CD,∠A=∠F,∠D=∠E,DE与AB,AF分别交于点G,O.试说明∠EOF的度数是一个定值,并求出这个定值.21·世纪*教育网
9.如图,已知CE为△ABC的外角∠ACD的平分线,CE交BA的延长线于点E.试说明∠BAC>∠B.21教育网

参考答案
【基础训练】
1.【答案】B
2.【答案】B
解：先根据∠1是△ACD的外角,可得∠1>∠A,再根据∠2是△CDE的外角,可得∠2>∠1,进而可得出结论.2·1·c·n·j·y
3.【答案】A
4.【答案】C
解：这个三角形中最大内角的度数为180°×>180°×=90°,所以这个三角形是钝角三角形.
5.【答案】75°
6.(1)证明:由题意知,△ACB是等腰直角三角形,且∠ACB=∠DCE=90°,∠B=45°.∵CF平分∠DCE,www-2-1-cnjy-com
∴∠DCF=∠ECF=45°,∴∠B=∠ECF,∴CF∥AB.
(2)解:由题意知,∠E=60°, 由(1)知,∠ECF=45°.∴∠DFC=∠ECF+∠E=45°+60°=105°.2-1-c-n-j-y
【培优提升】
1.【答案】C
解：如图所示,∠1=∠A+∠B,由题意可知,∠1+∠A+∠B=180°,所以∠1=90°,所以∠ACB=90°.【来源：21cnj*y.co*m】
2.【答案】D
3.【答案】D
解：根据平行线的性质定理、三角形内角和定理及推论可得:∠3+∠7=∠5+∠7>180°.
4.【答案】C
解：∵∠DBC=(∠A+∠ACB),
∠DCB=(∠A+∠ABC),
∴∠DBC+∠DCB=(∠A+180°),
又∵∠DBC+∠DCB=180°-∠BDC,
∴(∠A+180°)=180°-m.
∴∠A=180°-2m.
本题中,∠BDC与∠A的关系是∠BDC=90°-∠A.
5.【答案】①②③④
6.解:因为∠A+∠B+∠ACB=180°,∠B=67°,∠ACB=74°,所以∠A=180°-67°-74°=39°.21世纪教育网版权所有
所以∠BDF=∠A+∠AED=39°+48°=87°.
分析：先根据三角形的内角和定理求出∠A的度数,再根据三角形外角的性质求出∠BDF的度数.
7.解法一:如图(1),连接 ED,设AD与CE交于点H.因为在△BDE中,∠B+∠BED+∠BDE=180°,∠BED=∠BEC+∠CED,∠BDE=∠BDA+∠ADE,所以∠B+∠BDA+∠BEC+∠ADE+∠CED=180°.因为∠A+∠C+∠AHC=180°,∠CED+∠ADE+∠EHD=180°,∠AHC=∠EHD,所以∠A+∠C =∠ADE+∠CED,所以∠A+∠B+∠C+∠BDA+∠BEC=180°.21cnjy.com
(1)
(2)
解法二:如图(2),设AD与CE交于点H,易知∠1=∠B+∠E,∠2=∠1+∠D,所以∠B+∠E+∠D=∠2.因为在△ACH中,∠A+∠C+∠2=180°,所以∠A+∠C+∠B+∠D+∠E=180°.www.21-cn-jy.com
8. 解:因为∠EOF是△AOG的一个外角,所以∠EOF=∠A+∠AGO.因为AB∥CD,所以∠D=∠AGO,所以∠EOF=∠A+∠D.又因为∠A=∠F,∠D=∠E,所以∠EOF=∠E+∠F.在△EOF中,∠EOF+∠E+∠F=180°,所以∠EOF=90°,即∠EOF的度数是定值,为90°.21*cnjy*com
9.解:因为∠BAC是△ACE的外角,所以∠BAC>∠ACE,又因为CE平分∠ACD,所以∠ACE=∠DCE,所以∠BAC>∠DCE.【出处：21教育名师】
又因为∠DCE是△BCE的外角,所以∠DCE>∠B,所以∠BAC>∠B.