9.3 三角形的角平分线、中线和高 同步练习
文档属性
| 名称 | 9.3 三角形的角平分线、中线和高 同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 454.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-24 00:00:00 | ||
图片预览




文档简介
9.3 三角形的角平分线、中线和高
基础训练
1.下列说法正确的是( )
A.三角形的角平分线是射线
B.三角形的高是一条直线
C.三角形的三条中线相交于一点
D.三角形的中线是经过顶点和对边中点的直线
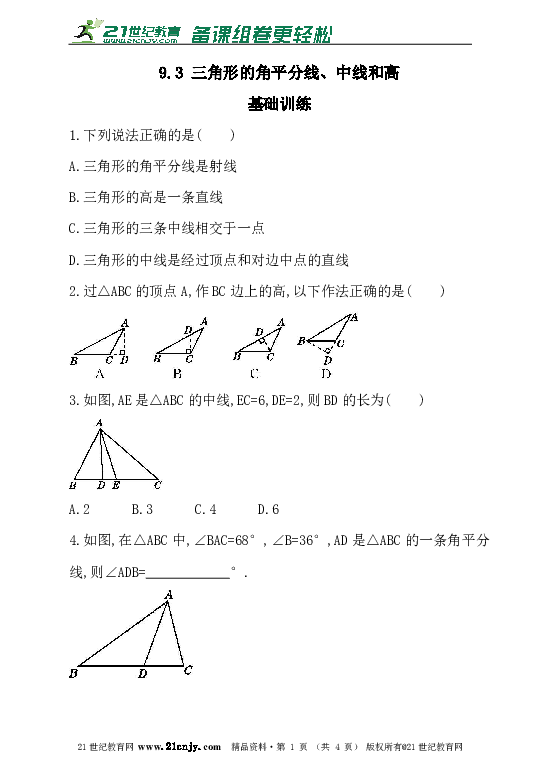
2.过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
3.如图,AE是△ABC的中线,EC=6,DE=2,则BD的长为( )
A.2 B.3 C.4 D.6
4.如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,则∠ADB=____________°.21cnjy.com
5.如图,在△ABC中,CD是AB边上的中线,线段AC比BC短2 cm,则△BCD和△ACD的周长的差是 cm.www-2-1-cnjy-com
6.如图,AD是△ABC的角平分线,DE∥AC交AB于E,EF∥AD交BC于F,试问EF是△BED的角平分线吗?为什么?2-1-c-n-j-y
培优提升
1.下列叙述中错误的是( )
A.三角形的中线、角平分线、高都是线段
B.三角形的三条高中至少有一条在三角形内部
C.只有一条高在三角形内部的三角形一定是钝角三角形
D.三角形的三条角平分线都在三角形内部
2.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于F,∠ABC=42°,∠A=60°,则∠BFC等于( )21世纪教育网版权所有
A.118° B.119° C.120° D.121°
3.如图,在△ABC中,D,E分别为BC,AD的中点,且△ABC的面积为4,则图中阴影部分的面积是( )【来源:21·世纪·教育·网】
A.2 B.1 C. D.
4.如图,△ABC中BC边上的高是________,△ACD中CD边上的高是________,△BCE中BC边上的高是________,以CF为高的三角形是________.21·cn·jy·com
5.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,BC=16,AD=6,BE=8,则AC=________.【来源:21cnj*y.co*m】
6.如图,△ABC中,∠ACB=110°,∠B=30°,作出∠BAC的平分线AE和BC边上的高AD,并求出∠DAE的度数.【出处:21教育名师】
7.如图,在△ABC中,AD是△ABC的角平分线,P为线段AD上的一个点,PE⊥AD交直线BC于点E.【版权所有:21教育】
(1)若∠B=30°,∠ACB=70°,则∠ADC= ,∠E= ;?
(2)若∠B=m°,∠ACB=n°,且n>m,请用含m,n的式子表示∠ADC,∠E的度数.
8.在等腰三角形ABC中,AB=AC,若一腰AC上的中线BD将等腰三角形ABC的周长分成15和6两部分,求三角形ABC的腰长及底边长.
参考答案
【基础训练】
1.【答案】C
解:任何一个三角形都有三条高、三条中线和三条角平分线,它们都是线段,不是射线或直线.
2.【答案】A
3.【答案】C
4.【答案】110
解:根据三角形的角平分线定义求得∠BAD=∠BAC=34°.∠ADC是△ABD的外角,故∠ADC=∠B+∠BAD=36°+34°=70°,所以∠ADB=180°-∠ADC=110°.21*cnjy*com
5.【答案】2
解:∵CD是AB边上的中线,∴AD=BD.
∵AC+2 cm=BC,
∴AC+AD+CD+2 cm=BC+BD+CD,
即△BCD与△ACD的周长的差为2 cm.
6.解:EF是△BED的角平分线.理由如下:如图,因为AD是△ABC的角平分线,所以∠1=∠2.因为EF∥AD,所以∠1=∠3,∠4=∠ADE.因为DE∥AC,所以∠2=∠ADE.所以∠2=∠4,所以∠3=∠4,所以EF是△BED的角平分线.21教育网
【培优提升】
1.【答案】C
解:直角三角形和钝角三角形都是只有一条高在三角形内部,故C错误.
2.【答案】C
3.【答案】B
解:因为D是BC的中点,所以△ABD与△ACD是等底同高的三角形,则S△ABD=S△ACD=S△ABC.同理可得S△AEC=S△DEC=S△ADC,所以S△AEC=S△ABC=×4=1.
4.【答案】AD;AD;BE;△ABC、△BCF和△ACF
5.【答案】12
解:由三角形面积公式可得S△ABC=BC·AD=AC·BE,所以16×6=8AC,所以AC=12.www.21-cn-jy.com
6.解:如图.
∵AD⊥BC,∴∠ADC=90°.
∵∠ACB+∠B+∠CAB=180°,∠ACB=110°,∠B=30°,
∴∠CAB=180°-110°-30°=40°.
∵AE平分∠CAB,
∴∠CAE=∠CAB=20°.
∵∠ACB是△ACD的外角,
∴∠DAC=∠ACB-∠ADC=110°-90°=20°.
∴∠DAE=∠DAC+∠CAE=40°.
7.解:(1)70°;20°
(2)∵∠B=m°,∠ACB=n°,
∠B+∠ACB+∠BAC=180°,
∴∠BAC=180°-m°-n°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=90°-m°-n°.
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=m°+90°-m°-n°=90°+m°-n°.
∵PE⊥AD,∴∠DPE=90°.
∴∠E=90°-∠ADC=90°-=
n°-m°.
8.解:设AB=AC=2x,则AD=CD=x.
(1)当AB+AD=15,BC+CD=6时,有2x+x=15,所以x=5,所以AB=AC=2x=10,BC=6-5=1.2·1·c·n·j·y
(2)当BC+CD=15,AB+AD=6时,有2x+x=6,所以x=2,AB=AC=2x=4,BC=13.因4+4<13,故不能组成三角形.21·世纪*教育网
所以三角形ABC的腰长为10,底边长为1.
基础训练
1.下列说法正确的是( )
A.三角形的角平分线是射线
B.三角形的高是一条直线
C.三角形的三条中线相交于一点
D.三角形的中线是经过顶点和对边中点的直线
2.过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
3.如图,AE是△ABC的中线,EC=6,DE=2,则BD的长为( )
A.2 B.3 C.4 D.6
4.如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,则∠ADB=____________°.21cnjy.com
5.如图,在△ABC中,CD是AB边上的中线,线段AC比BC短2 cm,则△BCD和△ACD的周长的差是 cm.www-2-1-cnjy-com
6.如图,AD是△ABC的角平分线,DE∥AC交AB于E,EF∥AD交BC于F,试问EF是△BED的角平分线吗?为什么?2-1-c-n-j-y
培优提升
1.下列叙述中错误的是( )
A.三角形的中线、角平分线、高都是线段
B.三角形的三条高中至少有一条在三角形内部
C.只有一条高在三角形内部的三角形一定是钝角三角形
D.三角形的三条角平分线都在三角形内部
2.如图,在△ABC中,∠ABC、∠ACB的平分线BE、CD相交于F,∠ABC=42°,∠A=60°,则∠BFC等于( )21世纪教育网版权所有
A.118° B.119° C.120° D.121°
3.如图,在△ABC中,D,E分别为BC,AD的中点,且△ABC的面积为4,则图中阴影部分的面积是( )【来源:21·世纪·教育·网】
A.2 B.1 C. D.
4.如图,△ABC中BC边上的高是________,△ACD中CD边上的高是________,△BCE中BC边上的高是________,以CF为高的三角形是________.21·cn·jy·com
5.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,BC=16,AD=6,BE=8,则AC=________.【来源:21cnj*y.co*m】
6.如图,△ABC中,∠ACB=110°,∠B=30°,作出∠BAC的平分线AE和BC边上的高AD,并求出∠DAE的度数.【出处:21教育名师】
7.如图,在△ABC中,AD是△ABC的角平分线,P为线段AD上的一个点,PE⊥AD交直线BC于点E.【版权所有:21教育】
(1)若∠B=30°,∠ACB=70°,则∠ADC= ,∠E= ;?
(2)若∠B=m°,∠ACB=n°,且n>m,请用含m,n的式子表示∠ADC,∠E的度数.
8.在等腰三角形ABC中,AB=AC,若一腰AC上的中线BD将等腰三角形ABC的周长分成15和6两部分,求三角形ABC的腰长及底边长.
参考答案
【基础训练】
1.【答案】C
解:任何一个三角形都有三条高、三条中线和三条角平分线,它们都是线段,不是射线或直线.
2.【答案】A
3.【答案】C
4.【答案】110
解:根据三角形的角平分线定义求得∠BAD=∠BAC=34°.∠ADC是△ABD的外角,故∠ADC=∠B+∠BAD=36°+34°=70°,所以∠ADB=180°-∠ADC=110°.21*cnjy*com
5.【答案】2
解:∵CD是AB边上的中线,∴AD=BD.
∵AC+2 cm=BC,
∴AC+AD+CD+2 cm=BC+BD+CD,
即△BCD与△ACD的周长的差为2 cm.
6.解:EF是△BED的角平分线.理由如下:如图,因为AD是△ABC的角平分线,所以∠1=∠2.因为EF∥AD,所以∠1=∠3,∠4=∠ADE.因为DE∥AC,所以∠2=∠ADE.所以∠2=∠4,所以∠3=∠4,所以EF是△BED的角平分线.21教育网
【培优提升】
1.【答案】C
解:直角三角形和钝角三角形都是只有一条高在三角形内部,故C错误.
2.【答案】C
3.【答案】B
解:因为D是BC的中点,所以△ABD与△ACD是等底同高的三角形,则S△ABD=S△ACD=S△ABC.同理可得S△AEC=S△DEC=S△ADC,所以S△AEC=S△ABC=×4=1.
4.【答案】AD;AD;BE;△ABC、△BCF和△ACF
5.【答案】12
解:由三角形面积公式可得S△ABC=BC·AD=AC·BE,所以16×6=8AC,所以AC=12.www.21-cn-jy.com
6.解:如图.
∵AD⊥BC,∴∠ADC=90°.
∵∠ACB+∠B+∠CAB=180°,∠ACB=110°,∠B=30°,
∴∠CAB=180°-110°-30°=40°.
∵AE平分∠CAB,
∴∠CAE=∠CAB=20°.
∵∠ACB是△ACD的外角,
∴∠DAC=∠ACB-∠ADC=110°-90°=20°.
∴∠DAE=∠DAC+∠CAE=40°.
7.解:(1)70°;20°
(2)∵∠B=m°,∠ACB=n°,
∠B+∠ACB+∠BAC=180°,
∴∠BAC=180°-m°-n°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=90°-m°-n°.
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=m°+90°-m°-n°=90°+m°-n°.
∵PE⊥AD,∴∠DPE=90°.
∴∠E=90°-∠ADC=90°-=
n°-m°.
8.解:设AB=AC=2x,则AD=CD=x.
(1)当AB+AD=15,BC+CD=6时,有2x+x=15,所以x=5,所以AB=AC=2x=10,BC=6-5=1.2·1·c·n·j·y
(2)当BC+CD=15,AB+AD=6时,有2x+x=6,所以x=2,AB=AC=2x=4,BC=13.因4+4<13,故不能组成三角形.21·世纪*教育网
所以三角形ABC的腰长为10,底边长为1.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
