第7章 一元一次不等式与不等式组 单元测试卷
文档属性
| 名称 | 第7章 一元一次不等式与不等式组 单元测试卷 | 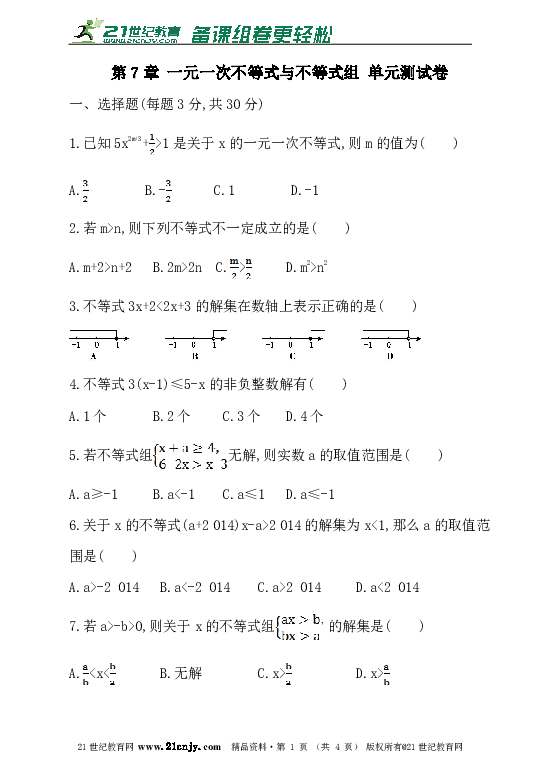 | |
| 格式 | zip | ||
| 文件大小 | 419.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-24 11:01:24 | ||
图片预览


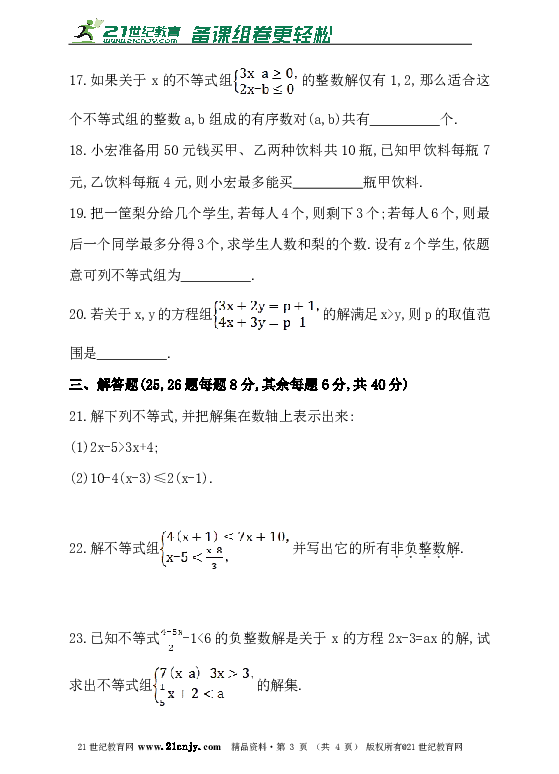

文档简介
第7章 一元一次不等式与不等式组 单元测试卷
一、选择题(每题3分,共30分)
1.已知5x2m+3+>1是关于x的一元一次不等式,则m的值为( )
A. B.- C.1 D.-1
2.若m>n,则下列不等式不一定成立的是( )
A.m+2>n+2 B.2m>2n C.> D.m2>n2
3.不等式3x+2<2x+3的解集在数轴上表示正确的是( )
4.不等式3(x-1)≤5-x的非负整数解有( )
A.1个 B.2个 C.3个 D.4个
5.若不等式组无解,则实数a的取值范围是( )
A.a≥-1 B.a<-1 C.a≤1 D.a≤-1
6.关于x的不等式(a+2 014)x-a>2 014的解集为x<1,那么a的取值范围是( )
A.a>-2 014 B.a<-2 014 C.a>2 014 D.a<2 014
7.若a>-b>0,则关于x的不等式组的解集是( )
A. D.x>
8.已知且-1A.-19.不等式组的解集是x>1,则m的取值范围是( )
A.m≥1 B.m≤1 C.m≥0 D.m≤0
10.某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )21教育网
A.103块 B.104块 C.105块 D.106块
二、填空题(每题3分,共30分)
11.写出一个解为x≥1的一元一次不等式:_____________.
12. 若a13.不等式组的所有整数解的和为___________.?
14.当x___________时,代数式1-的值不大于代数式的值.?
15.已知那么|x-3|+|x-1|=___________.
16.在实数范围内规定新运算“△”,其规则是:a△b=2a-b.已知不等式x△k≥1的解集表示在数轴上如图所示,则k的值是__________.
17.如果关于x的不等式组的整数解仅有1,2,那么适合这个不等式组的整数a,b组成的有序数对(a,b)共有__________个.
18.小宏准备用50元钱买甲、乙两种饮料共10瓶,已知甲饮料每瓶7元,乙饮料每瓶4元,则小宏最多能买__________瓶甲饮料.
19.把一筐梨分给几个学生,若每人4个,则剩下3个;若每人6个,则最后一个同学最多分得3个,求学生人数和梨的个数.设有z个学生,依题意可列不等式组为__________.21·世纪*教育网
20.若关于x,y的方程组的解满足x>y,则p的取值范围是__________.
三、解答题(25,26题每题8分,其余每题6分,共40分)
21.解下列不等式,并把解集在数轴上表示出来:
(1)2x-5>3x+4;
(2)10-4(x-3)≤2(x-1).
22.解不等式组并写出它的所有非负整数解.
23.已知不等式-1<6的负整数解是关于x的方程2x-3=ax的解,试求出不等式组的解集.
24.在某校班际篮球联赛中,每场比赛都要分出胜负,每队胜一场得3分,负一场得1分,如果某班要在第一轮的28场比赛中至少得43分,那么这个班至少要胜多少场?www-2-1-cnjy-com
25.某校七(2)班有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36千克,乙种制作材料29千克,制作A,B两种型号的陶艺品用料情况如下表:【来源:21cnj*y.co*m】
需甲种材料
需乙种材料
1件A型陶艺品
0.9千克
0.3千克
1件B型陶艺品
0.4千克
1千克
(1)设制作B型陶艺品x件,求x的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作A型和B型陶艺品的件数.
26.为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.21cnjy.com
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.www.21-cn-jy.com
参考答案
一、1.【答案】D 2.【答案】D 3.【答案】D
4.【答案】C 5.【答案】C 6.【答案】B
7.【答案】B
解:原不等式组可化为因为a>-b>0,所以<0,<0.而=<1,=>1,所以<,所以>,所以原不等式组无解,故选B.
8.【答案】D 9.【答案】D 10.【答案】C
二、11.【答案】x-1≥0(答案不唯一)
12.【答案】1<1-b<1-a
解:1-b,1-a都比1大,根据不等式的基本性质可知1-a比1-b大.
13.【答案】-2 14.【答案】≥
15.【答案】2
解:先求出不等式组的解集是116.【答案】-3
解:根据定义得到不等式2x-k≥1,从而得到x≥(k+1).由数轴知,不等式的解集是x≥-1,所以得方程(k+1)=-1,解得k=-3.
17.【答案】6
解:原不等式组可变形为所以≤x≤,因为不等式组仅有1,2两个整数解,所以0<≤1,2≤<3,从而解得018.【答案】3
解:设买x瓶甲饮料,则7x+4(10-x)≤50,解得x≤,所以最多能买3瓶甲饮料.
19.【答案】
20.【答案】p>-6
解:解方程组,得由题意可得p+5>-p-7,解得p>-6.
三、21.解:(1)移项,得2x-3x>4+5.合并同类项,得-x>9.系数化为1,得x<-9.在数轴上表示其解集如图①所示.21·cn·jy·com
①
②
(2)去括号、移项,得-4x-2x≤-2-10-12.合并同类项,得-6x≤-24.系数化为1,得x≥4.在数轴上表示其解集如图②所示.2·1·c·n·j·y
22.解:
由①得4x+4≤7x+10,
-3x≤6,x≥-2,
由②得3x-152x<7,x<,
所以-2≤x<,
所以非负整数解为0,1,2,3.
23.解:解不等式-1<6,得x>-2,其负整数解是x=-1,由题意,得2×(-1)-3=-a,所以a=5.2-1-c-n-j-y
所以原不等式组为解得分析:先求出不等式的负整数解,将其代入方程得到a的值,再将a的值代入不等式组,解不等式组即可.
24.解:设这个班要胜x场,根据题意得,3x+(28-x)≥43,解得x≥,所以这个班至少要胜8场.21*cnjy*com
25.解:(1)制作B型陶艺品x件,则制作A型陶艺品(50-x)件,由题意,得解得18≤x≤20.又因为x为正整数,所以x=18,19,20.【出处:21教育名师】
(2)由(1)知x=18,19,20,所以50-x=32,31,30,所以七(2)班制作A型和B型陶艺品的件数有三种可能:可能一:制作A型陶艺品32件,B型陶艺品18件;可能二:制作A型陶艺品31件,B型陶艺品19件;可能三:制作A型陶艺品30件,B型陶艺品20件.【版权所有:21教育】
解:题目中没有出现明显的表示不等关系的语句,分析题意可发现,制作两种型号的陶艺品的材料已给出限制,所用材料不能超过这个限制,因此我们就可以根据总材料的限制来列出本题的不等式组.
26.解:(1)设A型污水处理设备每周每台可以处理污水x t,B型污水处理设备每周每台可以处理污水y t,由题意得21教育名师原创作品
解得
即A型污水处理设备每周每台可以处理污水240 t,B型污水处理设备每周每台可以处理污水200 t.
(2)设购买A型污水处理设备m台,则购买B型污水处理设备(20-m)台,
则
解得12.5≤m≤15.
第一种方案:当m=13时,20-m=7,所需资金为13×12+7×10=226(万元);
第二种方案:当m=14时,20-m=6,所需资金为14×12+6×10=228(万元);
第三种方案:当m=15时,20-m=5,所需资金为15×12+5×10=230(万元);
即购买A型污水处理设备13台,购买B型污水处理设备7台时,所需资金最少,最少是226万元.
一、选择题(每题3分,共30分)
1.已知5x2m+3+>1是关于x的一元一次不等式,则m的值为( )
A. B.- C.1 D.-1
2.若m>n,则下列不等式不一定成立的是( )
A.m+2>n+2 B.2m>2n C.> D.m2>n2
3.不等式3x+2<2x+3的解集在数轴上表示正确的是( )
4.不等式3(x-1)≤5-x的非负整数解有( )
A.1个 B.2个 C.3个 D.4个
5.若不等式组无解,则实数a的取值范围是( )
A.a≥-1 B.a<-1 C.a≤1 D.a≤-1
6.关于x的不等式(a+2 014)x-a>2 014的解集为x<1,那么a的取值范围是( )
A.a>-2 014 B.a<-2 014 C.a>2 014 D.a<2 014
7.若a>-b>0,则关于x的不等式组的解集是( )
A.
8.已知且-1
A.m≥1 B.m≤1 C.m≥0 D.m≤0
10.某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )21教育网
A.103块 B.104块 C.105块 D.106块
二、填空题(每题3分,共30分)
11.写出一个解为x≥1的一元一次不等式:_____________.
12. 若a
14.当x___________时,代数式1-的值不大于代数式的值.?
15.已知那么|x-3|+|x-1|=___________.
16.在实数范围内规定新运算“△”,其规则是:a△b=2a-b.已知不等式x△k≥1的解集表示在数轴上如图所示,则k的值是__________.
17.如果关于x的不等式组的整数解仅有1,2,那么适合这个不等式组的整数a,b组成的有序数对(a,b)共有__________个.
18.小宏准备用50元钱买甲、乙两种饮料共10瓶,已知甲饮料每瓶7元,乙饮料每瓶4元,则小宏最多能买__________瓶甲饮料.
19.把一筐梨分给几个学生,若每人4个,则剩下3个;若每人6个,则最后一个同学最多分得3个,求学生人数和梨的个数.设有z个学生,依题意可列不等式组为__________.21·世纪*教育网
20.若关于x,y的方程组的解满足x>y,则p的取值范围是__________.
三、解答题(25,26题每题8分,其余每题6分,共40分)
21.解下列不等式,并把解集在数轴上表示出来:
(1)2x-5>3x+4;
(2)10-4(x-3)≤2(x-1).
22.解不等式组并写出它的所有非负整数解.
23.已知不等式-1<6的负整数解是关于x的方程2x-3=ax的解,试求出不等式组的解集.
24.在某校班际篮球联赛中,每场比赛都要分出胜负,每队胜一场得3分,负一场得1分,如果某班要在第一轮的28场比赛中至少得43分,那么这个班至少要胜多少场?www-2-1-cnjy-com
25.某校七(2)班有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36千克,乙种制作材料29千克,制作A,B两种型号的陶艺品用料情况如下表:【来源:21cnj*y.co*m】
需甲种材料
需乙种材料
1件A型陶艺品
0.9千克
0.3千克
1件B型陶艺品
0.4千克
1千克
(1)设制作B型陶艺品x件,求x的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作A型和B型陶艺品的件数.
26.为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.21cnjy.com
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.www.21-cn-jy.com
参考答案
一、1.【答案】D 2.【答案】D 3.【答案】D
4.【答案】C 5.【答案】C 6.【答案】B
7.【答案】B
解:原不等式组可化为因为a>-b>0,所以<0,<0.而=<1,=>1,所以<,所以>,所以原不等式组无解,故选B.
8.【答案】D 9.【答案】D 10.【答案】C
二、11.【答案】x-1≥0(答案不唯一)
12.【答案】1<1-b<1-a
解:1-b,1-a都比1大,根据不等式的基本性质可知1-a比1-b大.
13.【答案】-2 14.【答案】≥
15.【答案】2
解:先求出不等式组的解集是1
解:根据定义得到不等式2x-k≥1,从而得到x≥(k+1).由数轴知,不等式的解集是x≥-1,所以得方程(k+1)=-1,解得k=-3.
17.【答案】6
解:原不等式组可变形为所以≤x≤,因为不等式组仅有1,2两个整数解,所以0<≤1,2≤<3,从而解得0
解:设买x瓶甲饮料,则7x+4(10-x)≤50,解得x≤,所以最多能买3瓶甲饮料.
19.【答案】
20.【答案】p>-6
解:解方程组,得由题意可得p+5>-p-7,解得p>-6.
三、21.解:(1)移项,得2x-3x>4+5.合并同类项,得-x>9.系数化为1,得x<-9.在数轴上表示其解集如图①所示.21·cn·jy·com
①
②
(2)去括号、移项,得-4x-2x≤-2-10-12.合并同类项,得-6x≤-24.系数化为1,得x≥4.在数轴上表示其解集如图②所示.2·1·c·n·j·y
22.解:
由①得4x+4≤7x+10,
-3x≤6,x≥-2,
由②得3x-15
所以-2≤x<,
所以非负整数解为0,1,2,3.
23.解:解不等式-1<6,得x>-2,其负整数解是x=-1,由题意,得2×(-1)-3=-a,所以a=5.2-1-c-n-j-y
所以原不等式组为解得
24.解:设这个班要胜x场,根据题意得,3x+(28-x)≥43,解得x≥,所以这个班至少要胜8场.21*cnjy*com
25.解:(1)制作B型陶艺品x件,则制作A型陶艺品(50-x)件,由题意,得解得18≤x≤20.又因为x为正整数,所以x=18,19,20.【出处:21教育名师】
(2)由(1)知x=18,19,20,所以50-x=32,31,30,所以七(2)班制作A型和B型陶艺品的件数有三种可能:可能一:制作A型陶艺品32件,B型陶艺品18件;可能二:制作A型陶艺品31件,B型陶艺品19件;可能三:制作A型陶艺品30件,B型陶艺品20件.【版权所有:21教育】
解:题目中没有出现明显的表示不等关系的语句,分析题意可发现,制作两种型号的陶艺品的材料已给出限制,所用材料不能超过这个限制,因此我们就可以根据总材料的限制来列出本题的不等式组.
26.解:(1)设A型污水处理设备每周每台可以处理污水x t,B型污水处理设备每周每台可以处理污水y t,由题意得21教育名师原创作品
解得
即A型污水处理设备每周每台可以处理污水240 t,B型污水处理设备每周每台可以处理污水200 t.
(2)设购买A型污水处理设备m台,则购买B型污水处理设备(20-m)台,
则
解得12.5≤m≤15.
第一种方案:当m=13时,20-m=7,所需资金为13×12+7×10=226(万元);
第二种方案:当m=14时,20-m=6,所需资金为14×12+6×10=228(万元);
第三种方案:当m=15时,20-m=5,所需资金为15×12+5×10=230(万元);
即购买A型污水处理设备13台,购买B型污水处理设备7台时,所需资金最少,最少是226万元.
