2017年中考数学复习指导-利用几何变换求解多动点线段和的最值问题
文档属性
| 名称 | 2017年中考数学复习指导-利用几何变换求解多动点线段和的最值问题 |
|
|
| 格式 | zip | ||
| 文件大小 | 217.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-25 00:00:00 | ||
图片预览

文档简介
利用几何变换求解多动点线段和的最值问题
多动点产生的线段和的最值问题,涉及的知识面广,表现形式灵活,已成为中考的热点,也是考生颇感困惑的问题之一历年来,虽经命题者不断更新变化、赋予新意,但万变不离其宗,解题存在一定的规律与技巧,一般就是通过化归,利用对称、平移、旋转等几何变换,将相关线段转化到同一条直线上,达到化折为直的目的,再根据模型1——垂线段最短,或模型2——两点之间线段最短来求解.下面就不同情形举例分析.
一、求两动点到一定点距离和的最小值
此类问题一般借助轴对称变换,将定点所在直线同侧的两个动点中的一个对称变换
至直线的另一侧,利用模型1、2求解.
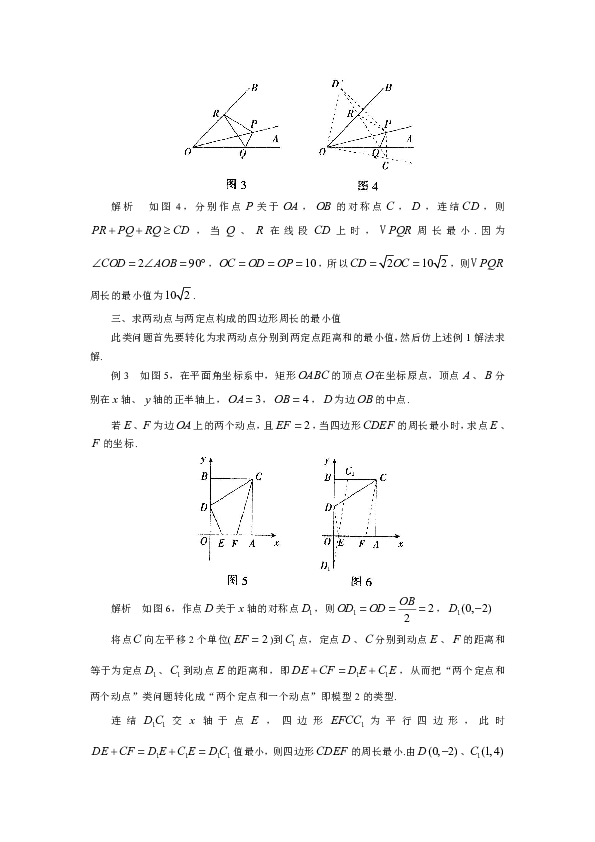
例1如图1,菱形的边长为,.
为上的一动点,为上的一动点,为上一个定点,则的最小值为
.
解析
如图2,根据菱形的对称性作点关于的对称点,连结,则有.所以,当点、、三点共线且垂直时最小.作点,所以的最小值即为为长.因为菱形的边长为,
,所以,,从而的最小值为.
二、求两动点与一定点构成的三角形周长的最小值
此类问题仍是借助轴对称变换,作定点关于两动点所在定直线的对称点,使两动点在两对称点的折线段上,利用模型2求解.
例2
如图3,,是内一点,,、分别是和上的动点,求周长的最小值.
解析
如图4,分别作点关于,的对称点,,连结,则,当、在线段上时,周长最小.因为,,所以,则
周长的最小值为.
三、求两动点与两定点构成的四边形周长的最小值
此类问题首先要转化为求两动点分别到两定点距离和的最小值,然后仿上述例1解法求解.
例3
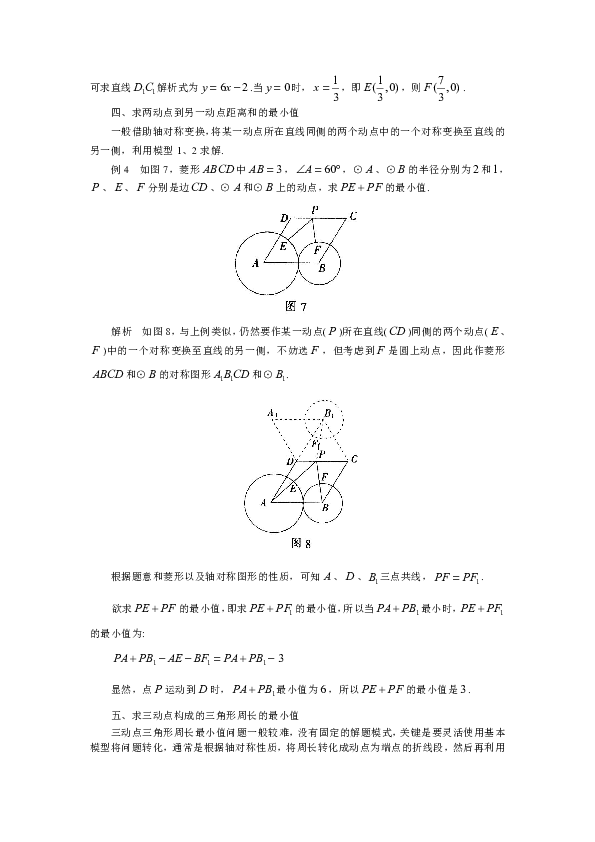
如图5,在平面角坐标系中,矩形的顶点在坐标原点,顶点、分别在轴、轴的正半轴上,,,为边的中点.
若、为边上的两个动点,且,当四边形的周长最小时,求点、的坐标.
解析
如图6,作点关于轴的对称点,则,
将点向左平移2个单位()到点,定点、分别到动点、的距离和等于为定点、到动点的距离和,即,从而把“两个定点和两个动点”类问题转化成“两个定点和一个动点”即模型2的类型.
连结交轴于点,四边形为平行四边形,此时值最小,则四边形的周长最小.由、可求直线解析式为.当时,,即,则.
四、求两动点到另一动点距离和的最小值
一般借助轴对称变换,将某一动点所在直线同侧的两个动点中的一个对称变换至直线的另一侧,利用模型1、2求解.
例4
如图7,菱形中,,⊙、⊙的半径分别为和,、、分别是边、⊙和⊙上的动点,求的最小值.
解析
如图8,与上例类似,仍然要作某一动点()所在直线()同侧的两个动点(、)中的一个对称变换至直线的另一侧,不妨选,但考虑到是圆上动点,因此作菱形和⊙的对称图形和⊙.
根据题意和菱形以及轴对称图形的性质,可知、、三点共线,.
欲求的最小值,即求的最小值,所以当最小时,的最小值为:
显然,点运动到时,最小值为,所以的最小值是.
五、求三动点构成的三角形周长的最小值
三动点三角形周长最小值问题一般较难,没有固定的解题模式,关键是要灵活使用基本模型将问题转化,通常是根据轴对称性质,将周长转化成动点为端点的折线段,然后再利用模型1,设法固定一个动点,将问题转化成双动点线段长最值问题,最后根据模型2求解.
例5
如图9,在平面直角坐标系中,已知,,.
点是线段上的动点(点不与、重合),点是线段上动点(点不与、重合),点是线段上动点(点不与、重合),求周长的最小值.
解析
如图10,不妨作关于的对称点,交于,作关于的对称点,交于,连结、、、.
由对称性可知:
,
当最小时,、、、四点共线,即、分别为与边、的交点,的最小值为.
由对称性可知
,,,
所以.
所以
(作等腰三角形底边的高,根据三线合一可得).
从条件不难发现为定值,根据模型1(垂线段最短),当(点即运动
到点)时,最小,从而最小.
又根据条件,不难求出
,,,,,
,
,
.
即最小值为:.
六、求三动点到一定点距离和的最小值
解决此类问题一般是应用旋转变换,将交于同一点的三条线段改变位置,等量转换为两定点之间的折线之和,然后利用模型1求解.
例6
如图11,四边形是边长为的正方形,为对角线上任意一点,当在何处时,最小,并求出最小值.
解析
如图12,将绕点逆时针旋转得到,连结,由旋转性质得,,为等边三角形,所以,此时转化为折线.根据模型2,
、、、四点共线时,最小,等于,所以位于与的交点处.
过点作的垂线交的延长线于点.由题意得,所以,.从而
.
即最小值是.
多动点产生的线段和的最值问题,涉及的知识面广,表现形式灵活,已成为中考的热点,也是考生颇感困惑的问题之一历年来,虽经命题者不断更新变化、赋予新意,但万变不离其宗,解题存在一定的规律与技巧,一般就是通过化归,利用对称、平移、旋转等几何变换,将相关线段转化到同一条直线上,达到化折为直的目的,再根据模型1——垂线段最短,或模型2——两点之间线段最短来求解.下面就不同情形举例分析.
一、求两动点到一定点距离和的最小值
此类问题一般借助轴对称变换,将定点所在直线同侧的两个动点中的一个对称变换
至直线的另一侧,利用模型1、2求解.
例1如图1,菱形的边长为,.
为上的一动点,为上的一动点,为上一个定点,则的最小值为
.
解析
如图2,根据菱形的对称性作点关于的对称点,连结,则有.所以,当点、、三点共线且垂直时最小.作点,所以的最小值即为为长.因为菱形的边长为,
,所以,,从而的最小值为.
二、求两动点与一定点构成的三角形周长的最小值
此类问题仍是借助轴对称变换,作定点关于两动点所在定直线的对称点,使两动点在两对称点的折线段上,利用模型2求解.
例2
如图3,,是内一点,,、分别是和上的动点,求周长的最小值.
解析
如图4,分别作点关于,的对称点,,连结,则,当、在线段上时,周长最小.因为,,所以,则
周长的最小值为.
三、求两动点与两定点构成的四边形周长的最小值
此类问题首先要转化为求两动点分别到两定点距离和的最小值,然后仿上述例1解法求解.
例3
如图5,在平面角坐标系中,矩形的顶点在坐标原点,顶点、分别在轴、轴的正半轴上,,,为边的中点.
若、为边上的两个动点,且,当四边形的周长最小时,求点、的坐标.
解析
如图6,作点关于轴的对称点,则,
将点向左平移2个单位()到点,定点、分别到动点、的距离和等于为定点、到动点的距离和,即,从而把“两个定点和两个动点”类问题转化成“两个定点和一个动点”即模型2的类型.
连结交轴于点,四边形为平行四边形,此时值最小,则四边形的周长最小.由、可求直线解析式为.当时,,即,则.
四、求两动点到另一动点距离和的最小值
一般借助轴对称变换,将某一动点所在直线同侧的两个动点中的一个对称变换至直线的另一侧,利用模型1、2求解.
例4
如图7,菱形中,,⊙、⊙的半径分别为和,、、分别是边、⊙和⊙上的动点,求的最小值.
解析
如图8,与上例类似,仍然要作某一动点()所在直线()同侧的两个动点(、)中的一个对称变换至直线的另一侧,不妨选,但考虑到是圆上动点,因此作菱形和⊙的对称图形和⊙.
根据题意和菱形以及轴对称图形的性质,可知、、三点共线,.
欲求的最小值,即求的最小值,所以当最小时,的最小值为:
显然,点运动到时,最小值为,所以的最小值是.
五、求三动点构成的三角形周长的最小值
三动点三角形周长最小值问题一般较难,没有固定的解题模式,关键是要灵活使用基本模型将问题转化,通常是根据轴对称性质,将周长转化成动点为端点的折线段,然后再利用模型1,设法固定一个动点,将问题转化成双动点线段长最值问题,最后根据模型2求解.
例5
如图9,在平面直角坐标系中,已知,,.
点是线段上的动点(点不与、重合),点是线段上动点(点不与、重合),点是线段上动点(点不与、重合),求周长的最小值.
解析
如图10,不妨作关于的对称点,交于,作关于的对称点,交于,连结、、、.
由对称性可知:
,
当最小时,、、、四点共线,即、分别为与边、的交点,的最小值为.
由对称性可知
,,,
所以.
所以
(作等腰三角形底边的高,根据三线合一可得).
从条件不难发现为定值,根据模型1(垂线段最短),当(点即运动
到点)时,最小,从而最小.
又根据条件,不难求出
,,,,,
,
,
.
即最小值为:.
六、求三动点到一定点距离和的最小值
解决此类问题一般是应用旋转变换,将交于同一点的三条线段改变位置,等量转换为两定点之间的折线之和,然后利用模型1求解.
例6
如图11,四边形是边长为的正方形,为对角线上任意一点,当在何处时,最小,并求出最小值.
解析
如图12,将绕点逆时针旋转得到,连结,由旋转性质得,,为等边三角形,所以,此时转化为折线.根据模型2,
、、、四点共线时,最小,等于,所以位于与的交点处.
过点作的垂线交的延长线于点.由题意得,所以,.从而
.
即最小值是.
同课章节目录
