苏科版数学八年级上册第6章一次函数 综合测评(含答案)
文档属性
| 名称 | 苏科版数学八年级上册第6章一次函数 综合测评(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 226.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-25 00:00:00 | ||
图片预览



文档简介
第6章
一次函数综合测评
时间:
满分:120分
班级:
姓名:
得分:
一、精心选一选(每小题3分,共24分)
1.
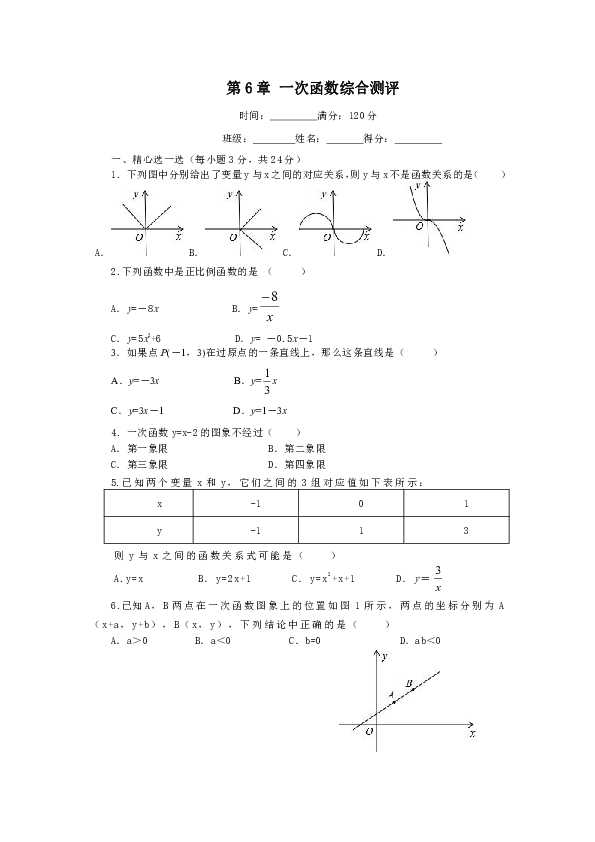
下列图中分别给出了变量y与x之间的对应关系,则y与x不是函数关系的是( )
A.
B.
C.
D.
2.下列函数中是正比例函数的是
(
)
A.y=-8x
B.y=
C.y=5x2+6
D.y=
-0.5x-1
3.如果点P(-1,3)在过原点的一条直线上,那么这条直线是(
)
A.y=-3x
B.y=x
C.y=3x-1
D.y=1-3x
4.
一次函数y=x-2的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.已知两个变量x和y,它们之间的3组对应值如下表所示:
x
-1
0
1
y
-1
1
3
则y与x之间的函数关系式可能是( )
A.y=x
B.y=2x+1
C.y=x2+x+1
D.y=
6.已知A,B两点在一次函数图象上的位置如图1所示,两点的坐标分别为A(x+a,y+b),B(x,y),下列结论中正确的是( )
A.a>0
B.a<0
C.b=0
D.ab<0
7.
在如图2所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A.
B.
C.
D.
8.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱中有油25升,途中加油若干升,加油前后汽车都以100千米/时的速度匀速行驶.已知油箱中的剩余油量y(升)与行驶时间t(时)之间的关系如图3所示,则下列说法错误的是(
)
A.加油前油箱中的剩余油量y(升)与行驶时间t(小时)的函数关系式是y=-8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还剩油6升
二、细心填一填(每小题4分,共32分)
9.已知函数y=(m-1)x|m|+2是一次函数,则m=_______
.
10.
已知一次函数y=mx+3中,y随x的增大而减小,写出符合题意的m的一个值
.
11.
函数y=2x+2的值为0时自变量的值为________,它是方程_______的解.
12.
甲、乙两人沿相同路线前往离学校12千米的地方参加植树活动,图4中、分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶______千米.
13.
某公司销售人员的个人月收入与其每月的销售量成一次函数关系,其图象如图5所示,则此销售人员的销售量为3千件时的月收入是_________元.
14.
一次函数y=x+2的图象与坐标轴围成的封闭图形的周长是___________.(结果保留根号)
15.
如图6,直线y=-x+4与x轴交于点A,与y轴交于点B,正方形OCDE的顶点C,E,D分别在边OA,OB,AB上,则点D的坐标为____________.
16.
某市出租车的收费标准是:起步价7元(即行驶距离不超过3千米需付7元车费),超过3千米以后,每增加1千米,加收2元(不足1千米按1千米计).小王乘该市出租车从甲地到乙地共支付车费19元,那么小王乘车路程的最大值是__________.
三、耐心做一做(共64分)
17.(8分)如图7,已知一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的表达式;
(2)试判断点B(-1,5),C(0,3)是否在这个一次函数的图象上.
18.(10分)填表并观察下列两个函数的变化情况.
x
1
2
3
4
5
…
y1=10+2x
y2=5x
(1)在同一个直角坐标系中画出这两个函数的图象;
(2)预测哪一个函数值先到100.
19.(10分)某生物小组观察一植物生长,得到植物高度y(厘米)与观察时间x(天)的关系,并画出如图8所示的图象(AC是线段,直线CD平行于x轴).
(1)该植物从观察时起,多少天以后停止长高?
(2)求AC的函数表达式,并求该植物最高增长多少厘米.
20.(10分)我们规定[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[2,k-2]的一次函数为正比例函数,求k的值;
(2)若一次函数与坐标轴的交点为A(0,-1),B(1,0),求这个一次函数的特征数.
21.(12分)阅读材料:一次函数y=kx+b(k≠0),
当自变量x增加1时,函数值y增加:
k(x+1)+b-(
kx+b)=k;
当自变量x增加2时,函数值y增加:
k(x+2)+b-(
kx+b)=2k;
当自变量x增加3时,函数值y增加:
k(x+3)+b-(
kx+b)=3k;
……
归纳:①一次函数中常数k的意义是自变量x增加1时,函数y的变化值;
②反之,若函数值y随自变量x均匀变化,则y与x是一次函数关系.
根据上述材料解答:
用同样大小的黑色棋子按如图9所示的规律摆放,则第2014个图中共有多少枚棋子?
22.(14分)某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图10所示.
请结合图象,回答下列问题:
(1)根据图中信息,请你写出一个结论;
(2)请问:前15位同学接水结束共需要几分钟
(3)小敏说:“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟.”你认为可能吗 请说明理由.
参考答案
一、
1.
B
2.A
3.
A
4.
B
5.
B
6.B
7.
D
8.
C
提示:易知选项A,B均正确;由图可知汽车每小时用油(25-9)÷2=8(升),所以汽车加油后还可行驶30÷8=3<4(小时),选项C错误;因为汽车从甲地到达乙地,所需时间为500÷100=5(小时),所以5小时耗油量为8×5=40(升).又因为汽车出发前油箱有油25升,途中加油21升,所以汽车到达乙地时油箱中还剩油:25+21-40=6(升),选项D正确.
二、9.
-1
10.答案不唯一,m<0的任意实数,如-2,-等
11.
-1
2x+2=0
12.
0.6
13.1400
14.
4+2
15.
D(2,2)
提示:因为四边形OCDE是正方形,所以可设D(x,x).因为D在直线y=-x+4上,所以x=-x+4,解得x=2.所以D(2,2).
16.
9千米
三、
17.
解:(1)将点(1,4)代入y=kx+3,得k+3=4,解得k=1.
所以该一次函数的表达式是y=x+3;
(2)由(1)知,一次函数的表达式是y=x+3.
当x=-1时,y=2,即点B(-1,5)不在该一次函数图象上;
当x=0时,y=3,即点C(0,3)在该一次函数图象上.
18.
解:(1)列表可得:
x
1
2
3
4
5
…
y1=10+2x
12
14
16
18
20
…
y2=5x
5
10
15
20
25
…
在同一个直角坐标系中画出这两个函数的图象如图所示:
(2)由函数的图象可知函数y2=5x的函数值先到100.
19.解:(1)根据图象可知,该植物从观察时起50天后停止长高;
(2)设AC的函数表达式是y=kx+b,则,解得,
所以AC的函数表达式是(0≤x≤50).
当x=50时,.
16-6=10.
所以该植物最高增长10厘米.
20.
解:(1)因为特征数为[2,k-2]的一次函数为y=2x+k-2,所以k-2=0,解得k=2;
(2)设一次函数的表达式为y=kx+b,将(1,0),(0,-1)分别代入y=kx+b,
得k+b=0,b=-1.解得k=1,b= 1.
所以一次函数的表达式为y=x-1.
所以一次函数的特征数为[1,-1].
21.解:因为相邻两个图形棋子个数依次增加3,即棋子个数与图形个数均匀变化,所以棋子个数y与图形个数x是一次函数关系.
设y=kx+b,因为x增加1,y增加3,所以k=3.所以y=3x+b.
把(1,4)代入y=3x+b,解得b=1.
所以y=3x+1.
当x=2014时,y=3×2014+1=6043.
所以第2014个图形中有6043枚棋子.
22.解:(1)结论不唯一,如一个水笼头一分钟流4升水.
(2)前2分钟,共流水16升,可供8位同学用;2分后,每分钟流4升水,还需(15-8)×2÷4=3.5(分).所以接水共需5.5分钟.
(3)可能.
理由:8位同学从1分时开始接水,到2分时接水8升,即4人水量,2分到4分一个水笼头出水8升,即4人水量.所以从1分到4分刚好3分钟.
S(千米)
t(分)
O
12
6
18
30
一次函数综合测评
时间:
满分:120分
班级:
姓名:
得分:
一、精心选一选(每小题3分,共24分)
1.
下列图中分别给出了变量y与x之间的对应关系,则y与x不是函数关系的是( )
A.
B.
C.
D.
2.下列函数中是正比例函数的是
(
)
A.y=-8x
B.y=
C.y=5x2+6
D.y=
-0.5x-1
3.如果点P(-1,3)在过原点的一条直线上,那么这条直线是(
)
A.y=-3x
B.y=x
C.y=3x-1
D.y=1-3x
4.
一次函数y=x-2的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.已知两个变量x和y,它们之间的3组对应值如下表所示:
x
-1
0
1
y
-1
1
3
则y与x之间的函数关系式可能是( )
A.y=x
B.y=2x+1
C.y=x2+x+1
D.y=
6.已知A,B两点在一次函数图象上的位置如图1所示,两点的坐标分别为A(x+a,y+b),B(x,y),下列结论中正确的是( )
A.a>0
B.a<0
C.b=0
D.ab<0
7.
在如图2所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A.
B.
C.
D.
8.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱中有油25升,途中加油若干升,加油前后汽车都以100千米/时的速度匀速行驶.已知油箱中的剩余油量y(升)与行驶时间t(时)之间的关系如图3所示,则下列说法错误的是(
)
A.加油前油箱中的剩余油量y(升)与行驶时间t(小时)的函数关系式是y=-8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达乙地时油箱中还剩油6升
二、细心填一填(每小题4分,共32分)
9.已知函数y=(m-1)x|m|+2是一次函数,则m=_______
.
10.
已知一次函数y=mx+3中,y随x的增大而减小,写出符合题意的m的一个值
.
11.
函数y=2x+2的值为0时自变量的值为________,它是方程_______的解.
12.
甲、乙两人沿相同路线前往离学校12千米的地方参加植树活动,图4中、分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶______千米.
13.
某公司销售人员的个人月收入与其每月的销售量成一次函数关系,其图象如图5所示,则此销售人员的销售量为3千件时的月收入是_________元.
14.
一次函数y=x+2的图象与坐标轴围成的封闭图形的周长是___________.(结果保留根号)
15.
如图6,直线y=-x+4与x轴交于点A,与y轴交于点B,正方形OCDE的顶点C,E,D分别在边OA,OB,AB上,则点D的坐标为____________.
16.
某市出租车的收费标准是:起步价7元(即行驶距离不超过3千米需付7元车费),超过3千米以后,每增加1千米,加收2元(不足1千米按1千米计).小王乘该市出租车从甲地到乙地共支付车费19元,那么小王乘车路程的最大值是__________.
三、耐心做一做(共64分)
17.(8分)如图7,已知一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的表达式;
(2)试判断点B(-1,5),C(0,3)是否在这个一次函数的图象上.
18.(10分)填表并观察下列两个函数的变化情况.
x
1
2
3
4
5
…
y1=10+2x
y2=5x
(1)在同一个直角坐标系中画出这两个函数的图象;
(2)预测哪一个函数值先到100.
19.(10分)某生物小组观察一植物生长,得到植物高度y(厘米)与观察时间x(天)的关系,并画出如图8所示的图象(AC是线段,直线CD平行于x轴).
(1)该植物从观察时起,多少天以后停止长高?
(2)求AC的函数表达式,并求该植物最高增长多少厘米.
20.(10分)我们规定[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[2,k-2]的一次函数为正比例函数,求k的值;
(2)若一次函数与坐标轴的交点为A(0,-1),B(1,0),求这个一次函数的特征数.
21.(12分)阅读材料:一次函数y=kx+b(k≠0),
当自变量x增加1时,函数值y增加:
k(x+1)+b-(
kx+b)=k;
当自变量x增加2时,函数值y增加:
k(x+2)+b-(
kx+b)=2k;
当自变量x增加3时,函数值y增加:
k(x+3)+b-(
kx+b)=3k;
……
归纳:①一次函数中常数k的意义是自变量x增加1时,函数y的变化值;
②反之,若函数值y随自变量x均匀变化,则y与x是一次函数关系.
根据上述材料解答:
用同样大小的黑色棋子按如图9所示的规律摆放,则第2014个图中共有多少枚棋子?
22.(14分)某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图10所示.
请结合图象,回答下列问题:
(1)根据图中信息,请你写出一个结论;
(2)请问:前15位同学接水结束共需要几分钟
(3)小敏说:“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟.”你认为可能吗 请说明理由.
参考答案
一、
1.
B
2.A
3.
A
4.
B
5.
B
6.B
7.
D
8.
C
提示:易知选项A,B均正确;由图可知汽车每小时用油(25-9)÷2=8(升),所以汽车加油后还可行驶30÷8=3<4(小时),选项C错误;因为汽车从甲地到达乙地,所需时间为500÷100=5(小时),所以5小时耗油量为8×5=40(升).又因为汽车出发前油箱有油25升,途中加油21升,所以汽车到达乙地时油箱中还剩油:25+21-40=6(升),选项D正确.
二、9.
-1
10.答案不唯一,m<0的任意实数,如-2,-等
11.
-1
2x+2=0
12.
0.6
13.1400
14.
4+2
15.
D(2,2)
提示:因为四边形OCDE是正方形,所以可设D(x,x).因为D在直线y=-x+4上,所以x=-x+4,解得x=2.所以D(2,2).
16.
9千米
三、
17.
解:(1)将点(1,4)代入y=kx+3,得k+3=4,解得k=1.
所以该一次函数的表达式是y=x+3;
(2)由(1)知,一次函数的表达式是y=x+3.
当x=-1时,y=2,即点B(-1,5)不在该一次函数图象上;
当x=0时,y=3,即点C(0,3)在该一次函数图象上.
18.
解:(1)列表可得:
x
1
2
3
4
5
…
y1=10+2x
12
14
16
18
20
…
y2=5x
5
10
15
20
25
…
在同一个直角坐标系中画出这两个函数的图象如图所示:
(2)由函数的图象可知函数y2=5x的函数值先到100.
19.解:(1)根据图象可知,该植物从观察时起50天后停止长高;
(2)设AC的函数表达式是y=kx+b,则,解得,
所以AC的函数表达式是(0≤x≤50).
当x=50时,.
16-6=10.
所以该植物最高增长10厘米.
20.
解:(1)因为特征数为[2,k-2]的一次函数为y=2x+k-2,所以k-2=0,解得k=2;
(2)设一次函数的表达式为y=kx+b,将(1,0),(0,-1)分别代入y=kx+b,
得k+b=0,b=-1.解得k=1,b= 1.
所以一次函数的表达式为y=x-1.
所以一次函数的特征数为[1,-1].
21.解:因为相邻两个图形棋子个数依次增加3,即棋子个数与图形个数均匀变化,所以棋子个数y与图形个数x是一次函数关系.
设y=kx+b,因为x增加1,y增加3,所以k=3.所以y=3x+b.
把(1,4)代入y=3x+b,解得b=1.
所以y=3x+1.
当x=2014时,y=3×2014+1=6043.
所以第2014个图形中有6043枚棋子.
22.解:(1)结论不唯一,如一个水笼头一分钟流4升水.
(2)前2分钟,共流水16升,可供8位同学用;2分后,每分钟流4升水,还需(15-8)×2÷4=3.5(分).所以接水共需5.5分钟.
(3)可能.
理由:8位同学从1分时开始接水,到2分时接水8升,即4人水量,2分到4分一个水笼头出水8升,即4人水量.所以从1分到4分刚好3分钟.
S(千米)
t(分)
O
12
6
18
30
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
