广西钦州市钦州港经济技术开发区中学2016-2017学年度高二文科数学下学期3月份考试试题(解析版)
文档属性
| 名称 | 广西钦州市钦州港经济技术开发区中学2016-2017学年度高二文科数学下学期3月份考试试题(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-27 00:00:00 | ||
图片预览


文档简介
广西钦州市钦州港经济技术开发区中学2016-2017学年度高二文科数学下学期3月份考试试题解析版
一、
选择题
1.
下列关于回归分析与独立性检验的说法正确的是(
)
A.回归分析和独立性检验没有什么区别
B.回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定关系
C.回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验
D.独立性检验可以100%确定两个变量之间是否具有某种关系
解析:
回归分析是对两个变量之间的相关关
( http: / / www.21cnjy.com )系的一种分析,而相关关系是一种不确定的关系,通过回归分析可以确定两个变量之间具有的近似关系;而独立性检验是对两个变量之间是否具有某种关系的分析,并且可以分析这两个变量在多大程度上具有这种关系,但不能100%肯定这种关系.
答案:
C
2.
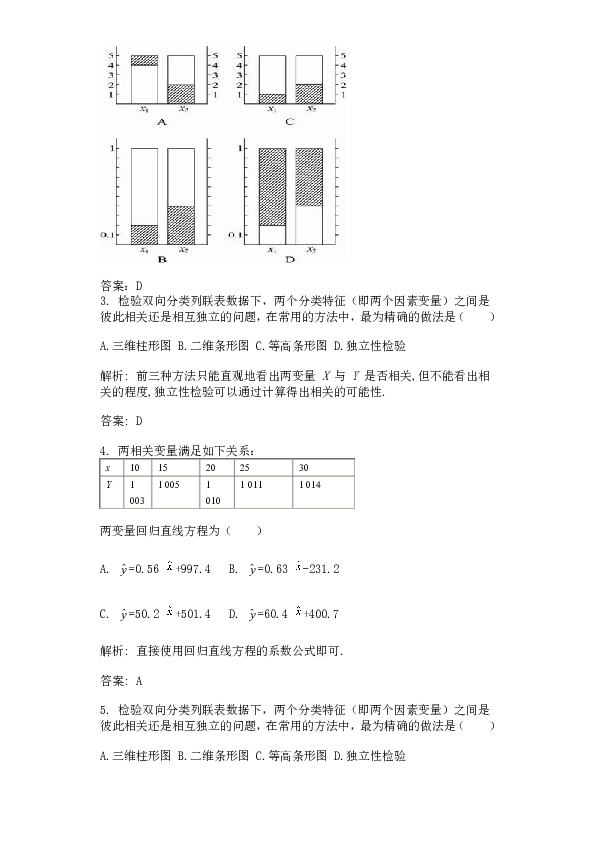
根据下面列联表作出的条形图中正确的有…( )
y
1
y
2
总 计
x
1
1
5
x
2
2
总 计
10
( http: / / www.21cnjy.com )
答案:D
3.
检验双向分类列联表数据下,两个分类特征(即两个因素变量)之间是彼此相关还是相互独立的问题,在常用的方法中,最为精确的做法是( )
A.三维柱形图
B.二维条形图
C.等高条形图
D.独立性检验
解析:
前三种方法只能直观地看出两变量
X
与
Y
是否相关,但不能看出相关的程度,独立性检验可以通过计算得出相关的可能性.
答案:
D
4.
两相关变量满足如下关系:
x
10
15
20
25
30
Y
1
003
1
005
1
010
1
011
1
014
两变量回归直线方程为( )
A.
=0.56
+997.4
B.
=0.63
-231.2
C.
=50.2
+501.4
D.
=60.4
+400.7
解析:
直接使用回归直线方程的系数公式即可.
答案:
A
5.
检验双向分类列联表数据下,两个分类特征(即两个因素变量)之间是彼此相关还是相互独立的问题,在常用的方法中,最为精确的做法是( )
A.三维柱形图
B.二维条形图
C.等高条形图
D.独立性检验
解析:前三种方法只能直观地看出两变量
X
与
Y
是否相关,但不能看出相关的程度,独立性检验可以通过计算得出相关的可能性.
答案:D
6.
某化工厂为预测某产品的回收率
y
,需要研究它和原料有效成份含量
x
之间的相关关系,现取了8对观察值,计算得
=52,
=228,
=478,
=1
849,则
y
对
x
的回归方程是( )
A.
=11.47+2.62
x
B.
=-11.47+2.62
x
C.
=2.62+11.47
x
D.
=11.47-2.62
x
答案:A
7.
在二维条形图中,两个比值
相差越大,要推断的论述成立的可能性就越大.( )
A.
与
B.
与
C.
与
D.
与
解析:
与
相差越大,说明
ad
与
bc
相差越大(即主对角线与副对角线乘积相差越大),则推断的论述成立的可能性就越大.
答案:
A
8.
根据下表可知,K
2
等于( )
y
1
y
2
总 计
x
1
20
100
x
2
70
总 计
200
A.43.3
B.2.67
C.53.3
D.23.3
答案:B
9.
关于下面等高条形图说法正确的有…( )
( http: / / www.21cnjy.com )
A.在被调查的
x
1
中,
y
1
占70%
B.在被调查的
x
2
中,
y
2
占20%
C.
x
1
与
y
1
有关
D.以上都不对
答案:A
10.
如果有95%的把握说事件A和B有关,那么具体算出的数据满足(
)
A.K
2
>3.841
B.K
2
<
3.841
C
.K
2
>6.635
D.K
2
<6.635
解析:
利用两个临界值来判断.若有95%的把握说事件A和B有关,则K
2
>3.841.
答案:
A
11.
在三维柱形图中,主对角线上两个柱形高度的乘积与副对角线上的两个柱形高度的乘积相差越大两个变量有关系的可能性就……( )
A.越大 B.越小
C.无法判断
D.以上都不对
答案:A
12.
若某地财政收入
x
与支出
Y
满
( http: / / www.21cnjy.com )足线性回归方程
Y
=
bx
+
a
+
e
(单位:亿元),其中
b
=0.8,
a
=2,|
e
|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
A.10亿
B.9亿
C.10.5亿
D.9.5亿
解析:
代入数据
y
=10+
e
,因为|
e
|<0.5,所以|
y
|≤10.5,故不会超过10.5亿.
答案:
C
二、
填空题
13.
计算下面事件A与事件B的2×2列联表的χ
2
统计量值,得χ
2
≈________,从而得出结论________.
B
总计
A
39
157
196
29
167
196
总计
68
324
392
答案:
1.779 没有充分的证据显示两者有关系
【解析】χ
2
=
≈1.779.
∵1.779<2.076,∴没有充分的证据显示两者有关系.
14.
三维柱形图与独立性检验判断两个分类变量是否有关系,哪一个能更精确地判断可能程度:
.
答案:独立性检验
15.
对于左边2×2列联表,在二维条形图中,两个比例的值
与
相差越大,
H
:“
x
与
Y
有关系”的可能性
.
答案:越大
16.
有甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
优秀
不优秀
总计
甲班
10
35
45
乙班
7
38
45
总计
17
73
90
利用列联表的独立性检验估计,成绩与班级_________(填有或无)关系.
解析:
成绩与班级有无关系,就是看随机变量的值与临界值2.706的大小关系.
由公式求得K
2
=
≈0.653<2.706,所以成绩与班级无关系.
答案:
无
解答题
17.
依据上题中列联表中的数据画出三维柱形图、二维条形图、等高条形图,并对图形进行分析.
答案:
解:
(1)三维柱形图:
( http: / / www.21cnjy.com )
比较来说,底面副对角线上两个柱体高度乘积要大一些,因此可以在某种程度上认为“喜欢玩电脑游戏与认为作业量的多少有关”.
( http: / / www.21cnjy.com )
(2)二维条形图:
在二维条形图中,可以估计喜欢玩电脑游戏的学
( http: / / www.21cnjy.com )生中认为作业多的人所占的比例与不喜欢玩电脑游戏的学生中认为作业多的人所占的比例,两个比例的值相差越大,
相关的可能性就越大.
(3)等高条形图:
( http: / / www.21cnjy.com )
等高条形图清晰地反映两种情况下认为作业量多少的比例.
18.
为研究造成死亡的结核病类型与性别的关系,取得如下资料:
男 性
女 性
呼吸系统结核
3
534
1
319
能造成死亡的结核病类型
270
252
由此你能得出什么结论
解
:
首先利用已知数据完成列联表:
男 性
女 性
总 计
呼吸系统结核
3
534
1
319
4
853
能造成死亡的结核病类型
270
252
522
总 计
3
804
1
571
5
375
根据列联表数据计算可得
K
2
=
=101.4>10.828.
由此可以肯定结核病造成的死亡与性别有关系.
19.
下面表格是两种教学实验的成绩对比统计,试分析两种教法的效果.
及格
不及格
合计
掌握教学法
36
8
44
常规教学法
40
16
56
合计
76
24
100
解析:
比较两种教学法的效果,就是看两种教学法对学生成绩的效果是否相关.
解:由公式求得K
2
=
≈1.458<2.706,故这两种教学方法对学生成绩的效果是相互独立的.
20.
为了测试某药物的预
( http: / / www.21cnjy.com )防效果,进行动物试验,发现在测试的50只未服药的动物中有20只患病,60只服药的动物中有10只患病.分别利用图形和独立性检验的方法判断药物是否有效
你得到的结论在什么范围内有效
答案:解:根据题目所给数据得到如下列联表:
不患病
患 病
总 计
服 药
50
10
60
未服药
30
20
50
总 计
80
30
110
作出相应的二维条形图,其中
表示不患病,
表示患病,从图中可以看出,未服药中患病的比例高于服药中患病的比例,因此,这种药物有效.
( http: / / www.21cnjy.com )
又∵K
2
=
≈7.486>6.635,
∴有99%的把握认为该药有效.
21.
某城市一个交通路口原来只设有红
( http: / / www.21cnjy.com )绿灯,平均每年发生交通事故80起,案件的破获率为70%.为了加强该路口的管理,第二年在该路口设置了电子摄像头,该年发生交通事故70起,共破获了56起,第三年的白天安排了交警执勤,该年发生交通事故60起,破获了54起.
(1)根据以上材料分析,加强管理后的两年该路口的交通状况发生了怎样的变化
(2)试采用独立性检验进行分析,电子摄像头和白天的民警执勤对该路口交通肇事案件的破获分别产生了什么样的影响
答案:
思路分析:
这是生活中一个
( http: / / www.21cnjy.com )很常见的例子,可以根据所提供数据,给出列联表,画出相应的二维条形图,首先判断安装电子摄像头及交警执勤对交通事故是否发生了影响,然后再根据独立性检验给出可信度的判断即可.
解
:
(1)由统计数据可知,没有
( http: / / www.21cnjy.com )采取措施之前,案件的发生较多,并且破获率只有70%,安装电子摄像头之后,案件的发生次数有所减少,并且破获率提高到了80%,白天安排交警执勤后,案件的发生频数进一步减少,并且破获率提高到了90%.由此可加,电子摄像头对遏制交通案件的发生起到了一定作用,并且给破案带来了一定的帮助,而安排交警执勤对这些影响更大.
(2)根据所提供的数据可以绘制对应的列联表如下:
破获的案件
未破获的案件
合计
未采取措施
56
24
80
安装摄像头
56
14
70
合计
112
38
150
破获的案件
未破获的案件
合计
未采取措施
56
24
80
交警白天执勤
54
6
60
合计
110
30
140
( http: / / www.21cnjy.com )
从条形图容易看出,安装电子摄像头后,破案率有
( http: / / www.21cnjy.com )了明显提高,而实行交警执勤后案件的破获率是最高的,这说明两种措施对案件的破获都起到了一定的积极作用.
先分析电子摄像头对破案的影响的可信度,令a=56,b=24,c=56,d=14,构造随机变量
K
2
=
=
≈1.97,
而查表可知,P(K
2
≥
( http: / / www.21cnjy.com )1.323)=0.25,且1-0.25=0.75=75%,因此至少有75%的把握认为,安装电子摄像头对案件的破获起到了作用.
再分析交警执勤的情况,同样令a=56,b=24,c=54,d=6,则
K
2
=
≈8.15,
而查表可知,P(K
2
( http: / / www.21cnjy.com )≥7.879)=0.005,且1-0.005=0.995=99.5%,因此至少有99.5%的把握认为,交警执勤对案件的破获起到了作用.
22.
1950~1958年我国的人口数据资料:
年份
x
1950
1951
1952
1953
1954
1955
1956
1957
1958
人数
Y
/万人
55
196
56
300
57
482
58
796
60
266
61
560
62
828
64
563
65
994
求
y
关于
x
的非线性回归方程.
解:根据收集数据,作散点图.
( http: / / www.21cnjy.com )
根据已有函数知识,发现样本点分布在某一条指数函数周围,
y
=
c
1
e
c
2
x
(其中
c
1
,
c
2
是待定参数).
令
z
=ln
y
,则有
y
=
e
z
,
∴
e
z
=
e
lnc
1
+
c
2
x
.
z
=
c
2
x
+ln
c
1
=
bx
+
a
,
变换后:
x
1950
1951
1952
1953
1954
1955
1956
1957
1958
z
=ln
y
10.92
10.94
10.96
10.98
11.01
11.03
11.05
11.08
11.09
由散点图可知,
x
与
z
线性相关,故采用一元线性回归模型,由表中数算得:
=1
954,L
xz
=
(
z
i
-
)=1.23,
=11.01,L
xx
=
=60.
∴
b
=
≈0.021.
a
=
-
b
=-30.02.
∴
=
a
+
bx
=0.021
x
-30.02,
即ln
y
=0.021
x
--30.02.
∴
y
=
e
0.021
x
-30.02
.
因此,所求非线性回归方程为
y
=
e
0.021
x
-30.02
.
点评:有些非线性的回归问题可化为线性问题来考虑,通过变换变量来实现.
一、
选择题
1.
下列关于回归分析与独立性检验的说法正确的是(
)
A.回归分析和独立性检验没有什么区别
B.回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定关系
C.回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验
D.独立性检验可以100%确定两个变量之间是否具有某种关系
解析:
回归分析是对两个变量之间的相关关
( http: / / www.21cnjy.com )系的一种分析,而相关关系是一种不确定的关系,通过回归分析可以确定两个变量之间具有的近似关系;而独立性检验是对两个变量之间是否具有某种关系的分析,并且可以分析这两个变量在多大程度上具有这种关系,但不能100%肯定这种关系.
答案:
C
2.
根据下面列联表作出的条形图中正确的有…( )
y
1
y
2
总 计
x
1
1
5
x
2
2
总 计
10
( http: / / www.21cnjy.com )
答案:D
3.
检验双向分类列联表数据下,两个分类特征(即两个因素变量)之间是彼此相关还是相互独立的问题,在常用的方法中,最为精确的做法是( )
A.三维柱形图
B.二维条形图
C.等高条形图
D.独立性检验
解析:
前三种方法只能直观地看出两变量
X
与
Y
是否相关,但不能看出相关的程度,独立性检验可以通过计算得出相关的可能性.
答案:
D
4.
两相关变量满足如下关系:
x
10
15
20
25
30
Y
1
003
1
005
1
010
1
011
1
014
两变量回归直线方程为( )
A.
=0.56
+997.4
B.
=0.63
-231.2
C.
=50.2
+501.4
D.
=60.4
+400.7
解析:
直接使用回归直线方程的系数公式即可.
答案:
A
5.
检验双向分类列联表数据下,两个分类特征(即两个因素变量)之间是彼此相关还是相互独立的问题,在常用的方法中,最为精确的做法是( )
A.三维柱形图
B.二维条形图
C.等高条形图
D.独立性检验
解析:前三种方法只能直观地看出两变量
X
与
Y
是否相关,但不能看出相关的程度,独立性检验可以通过计算得出相关的可能性.
答案:D
6.
某化工厂为预测某产品的回收率
y
,需要研究它和原料有效成份含量
x
之间的相关关系,现取了8对观察值,计算得
=52,
=228,
=478,
=1
849,则
y
对
x
的回归方程是( )
A.
=11.47+2.62
x
B.
=-11.47+2.62
x
C.
=2.62+11.47
x
D.
=11.47-2.62
x
答案:A
7.
在二维条形图中,两个比值
相差越大,要推断的论述成立的可能性就越大.( )
A.
与
B.
与
C.
与
D.
与
解析:
与
相差越大,说明
ad
与
bc
相差越大(即主对角线与副对角线乘积相差越大),则推断的论述成立的可能性就越大.
答案:
A
8.
根据下表可知,K
2
等于( )
y
1
y
2
总 计
x
1
20
100
x
2
70
总 计
200
A.43.3
B.2.67
C.53.3
D.23.3
答案:B
9.
关于下面等高条形图说法正确的有…( )
( http: / / www.21cnjy.com )
A.在被调查的
x
1
中,
y
1
占70%
B.在被调查的
x
2
中,
y
2
占20%
C.
x
1
与
y
1
有关
D.以上都不对
答案:A
10.
如果有95%的把握说事件A和B有关,那么具体算出的数据满足(
)
A.K
2
>3.841
B.K
2
<
3.841
C
.K
2
>6.635
D.K
2
<6.635
解析:
利用两个临界值来判断.若有95%的把握说事件A和B有关,则K
2
>3.841.
答案:
A
11.
在三维柱形图中,主对角线上两个柱形高度的乘积与副对角线上的两个柱形高度的乘积相差越大两个变量有关系的可能性就……( )
A.越大 B.越小
C.无法判断
D.以上都不对
答案:A
12.
若某地财政收入
x
与支出
Y
满
( http: / / www.21cnjy.com )足线性回归方程
Y
=
bx
+
a
+
e
(单位:亿元),其中
b
=0.8,
a
=2,|
e
|<0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
A.10亿
B.9亿
C.10.5亿
D.9.5亿
解析:
代入数据
y
=10+
e
,因为|
e
|<0.5,所以|
y
|≤10.5,故不会超过10.5亿.
答案:
C
二、
填空题
13.
计算下面事件A与事件B的2×2列联表的χ
2
统计量值,得χ
2
≈________,从而得出结论________.
B
总计
A
39
157
196
29
167
196
总计
68
324
392
答案:
1.779 没有充分的证据显示两者有关系
【解析】χ
2
=
≈1.779.
∵1.779<2.076,∴没有充分的证据显示两者有关系.
14.
三维柱形图与独立性检验判断两个分类变量是否有关系,哪一个能更精确地判断可能程度:
.
答案:独立性检验
15.
对于左边2×2列联表,在二维条形图中,两个比例的值
与
相差越大,
H
:“
x
与
Y
有关系”的可能性
.
答案:越大
16.
有甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
优秀
不优秀
总计
甲班
10
35
45
乙班
7
38
45
总计
17
73
90
利用列联表的独立性检验估计,成绩与班级_________(填有或无)关系.
解析:
成绩与班级有无关系,就是看随机变量的值与临界值2.706的大小关系.
由公式求得K
2
=
≈0.653<2.706,所以成绩与班级无关系.
答案:
无
解答题
17.
依据上题中列联表中的数据画出三维柱形图、二维条形图、等高条形图,并对图形进行分析.
答案:
解:
(1)三维柱形图:
( http: / / www.21cnjy.com )
比较来说,底面副对角线上两个柱体高度乘积要大一些,因此可以在某种程度上认为“喜欢玩电脑游戏与认为作业量的多少有关”.
( http: / / www.21cnjy.com )
(2)二维条形图:
在二维条形图中,可以估计喜欢玩电脑游戏的学
( http: / / www.21cnjy.com )生中认为作业多的人所占的比例与不喜欢玩电脑游戏的学生中认为作业多的人所占的比例,两个比例的值相差越大,
相关的可能性就越大.
(3)等高条形图:
( http: / / www.21cnjy.com )
等高条形图清晰地反映两种情况下认为作业量多少的比例.
18.
为研究造成死亡的结核病类型与性别的关系,取得如下资料:
男 性
女 性
呼吸系统结核
3
534
1
319
能造成死亡的结核病类型
270
252
由此你能得出什么结论
解
:
首先利用已知数据完成列联表:
男 性
女 性
总 计
呼吸系统结核
3
534
1
319
4
853
能造成死亡的结核病类型
270
252
522
总 计
3
804
1
571
5
375
根据列联表数据计算可得
K
2
=
=101.4>10.828.
由此可以肯定结核病造成的死亡与性别有关系.
19.
下面表格是两种教学实验的成绩对比统计,试分析两种教法的效果.
及格
不及格
合计
掌握教学法
36
8
44
常规教学法
40
16
56
合计
76
24
100
解析:
比较两种教学法的效果,就是看两种教学法对学生成绩的效果是否相关.
解:由公式求得K
2
=
≈1.458<2.706,故这两种教学方法对学生成绩的效果是相互独立的.
20.
为了测试某药物的预
( http: / / www.21cnjy.com )防效果,进行动物试验,发现在测试的50只未服药的动物中有20只患病,60只服药的动物中有10只患病.分别利用图形和独立性检验的方法判断药物是否有效
你得到的结论在什么范围内有效
答案:解:根据题目所给数据得到如下列联表:
不患病
患 病
总 计
服 药
50
10
60
未服药
30
20
50
总 计
80
30
110
作出相应的二维条形图,其中
表示不患病,
表示患病,从图中可以看出,未服药中患病的比例高于服药中患病的比例,因此,这种药物有效.
( http: / / www.21cnjy.com )
又∵K
2
=
≈7.486>6.635,
∴有99%的把握认为该药有效.
21.
某城市一个交通路口原来只设有红
( http: / / www.21cnjy.com )绿灯,平均每年发生交通事故80起,案件的破获率为70%.为了加强该路口的管理,第二年在该路口设置了电子摄像头,该年发生交通事故70起,共破获了56起,第三年的白天安排了交警执勤,该年发生交通事故60起,破获了54起.
(1)根据以上材料分析,加强管理后的两年该路口的交通状况发生了怎样的变化
(2)试采用独立性检验进行分析,电子摄像头和白天的民警执勤对该路口交通肇事案件的破获分别产生了什么样的影响
答案:
思路分析:
这是生活中一个
( http: / / www.21cnjy.com )很常见的例子,可以根据所提供数据,给出列联表,画出相应的二维条形图,首先判断安装电子摄像头及交警执勤对交通事故是否发生了影响,然后再根据独立性检验给出可信度的判断即可.
解
:
(1)由统计数据可知,没有
( http: / / www.21cnjy.com )采取措施之前,案件的发生较多,并且破获率只有70%,安装电子摄像头之后,案件的发生次数有所减少,并且破获率提高到了80%,白天安排交警执勤后,案件的发生频数进一步减少,并且破获率提高到了90%.由此可加,电子摄像头对遏制交通案件的发生起到了一定作用,并且给破案带来了一定的帮助,而安排交警执勤对这些影响更大.
(2)根据所提供的数据可以绘制对应的列联表如下:
破获的案件
未破获的案件
合计
未采取措施
56
24
80
安装摄像头
56
14
70
合计
112
38
150
破获的案件
未破获的案件
合计
未采取措施
56
24
80
交警白天执勤
54
6
60
合计
110
30
140
( http: / / www.21cnjy.com )
从条形图容易看出,安装电子摄像头后,破案率有
( http: / / www.21cnjy.com )了明显提高,而实行交警执勤后案件的破获率是最高的,这说明两种措施对案件的破获都起到了一定的积极作用.
先分析电子摄像头对破案的影响的可信度,令a=56,b=24,c=56,d=14,构造随机变量
K
2
=
=
≈1.97,
而查表可知,P(K
2
≥
( http: / / www.21cnjy.com )1.323)=0.25,且1-0.25=0.75=75%,因此至少有75%的把握认为,安装电子摄像头对案件的破获起到了作用.
再分析交警执勤的情况,同样令a=56,b=24,c=54,d=6,则
K
2
=
≈8.15,
而查表可知,P(K
2
( http: / / www.21cnjy.com )≥7.879)=0.005,且1-0.005=0.995=99.5%,因此至少有99.5%的把握认为,交警执勤对案件的破获起到了作用.
22.
1950~1958年我国的人口数据资料:
年份
x
1950
1951
1952
1953
1954
1955
1956
1957
1958
人数
Y
/万人
55
196
56
300
57
482
58
796
60
266
61
560
62
828
64
563
65
994
求
y
关于
x
的非线性回归方程.
解:根据收集数据,作散点图.
( http: / / www.21cnjy.com )
根据已有函数知识,发现样本点分布在某一条指数函数周围,
y
=
c
1
e
c
2
x
(其中
c
1
,
c
2
是待定参数).
令
z
=ln
y
,则有
y
=
e
z
,
∴
e
z
=
e
lnc
1
+
c
2
x
.
z
=
c
2
x
+ln
c
1
=
bx
+
a
,
变换后:
x
1950
1951
1952
1953
1954
1955
1956
1957
1958
z
=ln
y
10.92
10.94
10.96
10.98
11.01
11.03
11.05
11.08
11.09
由散点图可知,
x
与
z
线性相关,故采用一元线性回归模型,由表中数算得:
=1
954,L
xz
=
(
z
i
-
)=1.23,
=11.01,L
xx
=
=60.
∴
b
=
≈0.021.
a
=
-
b
=-30.02.
∴
=
a
+
bx
=0.021
x
-30.02,
即ln
y
=0.021
x
--30.02.
∴
y
=
e
0.021
x
-30.02
.
因此,所求非线性回归方程为
y
=
e
0.021
x
-30.02
.
点评:有些非线性的回归问题可化为线性问题来考虑,通过变换变量来实现.
