13.3.1等腰三角形 学案
图片预览
文档简介
《等腰三角形的性质》学案
班别
学号
姓名
一、学习目标
1、掌握等腰三角形的概念,等腰三角形的性质.
2、会运用性质,会进行简单的说理.
二、前置作业:
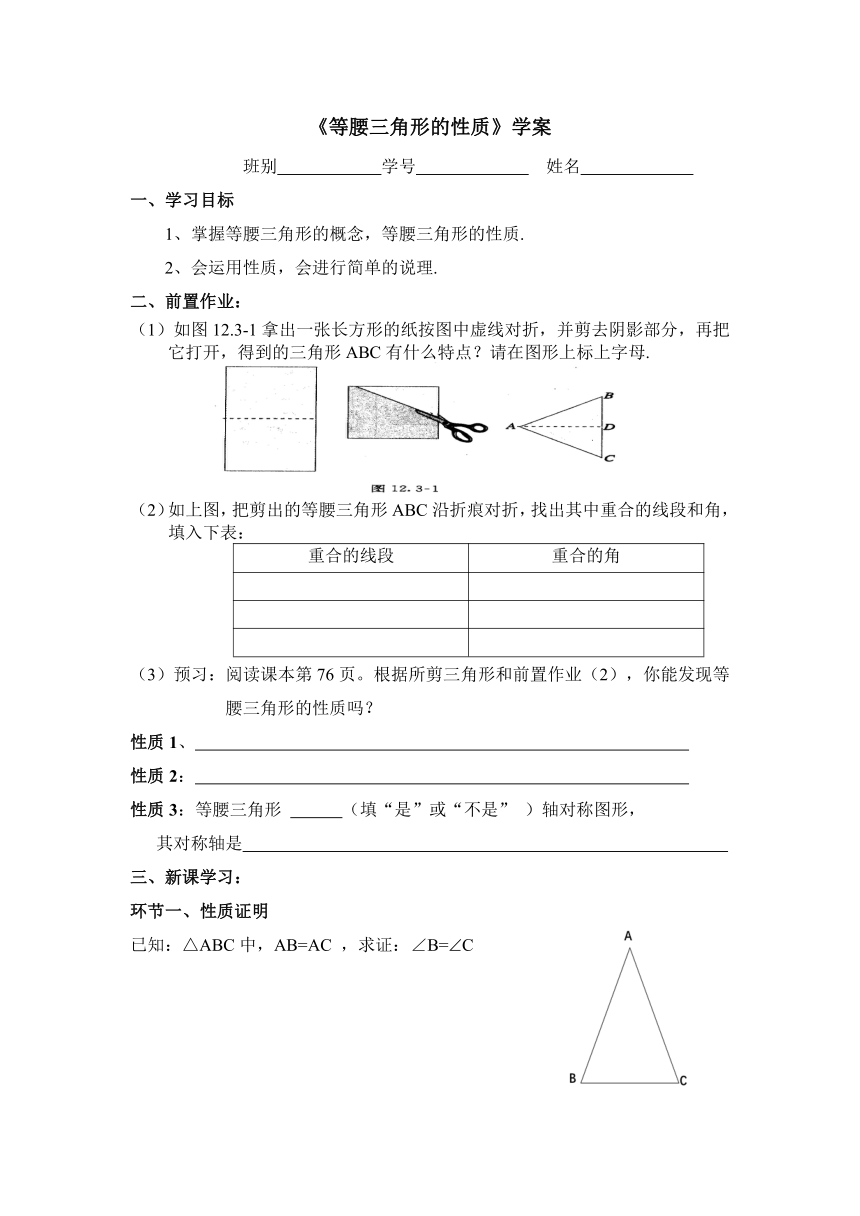
(1)如图12.3-1拿出一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它打开,得到的三角形ABC有什么特点?请在图形上标上字母.
(2)如上图,把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,
填入下表:
重合的线段
重合的角
(3)预习:阅读课本第76页。根据所剪三角形和前置作业(2),你能发现等腰三角形的性质吗?
性质1、
性质2:
性质3:等腰三角形
(填“是”或“不是”
)轴对称图形,
其对称轴是
三、新课学习:
环节一、性质证明
已知:△ABC中,AB=AC
,求证:∠B=C
环节二、性质运用
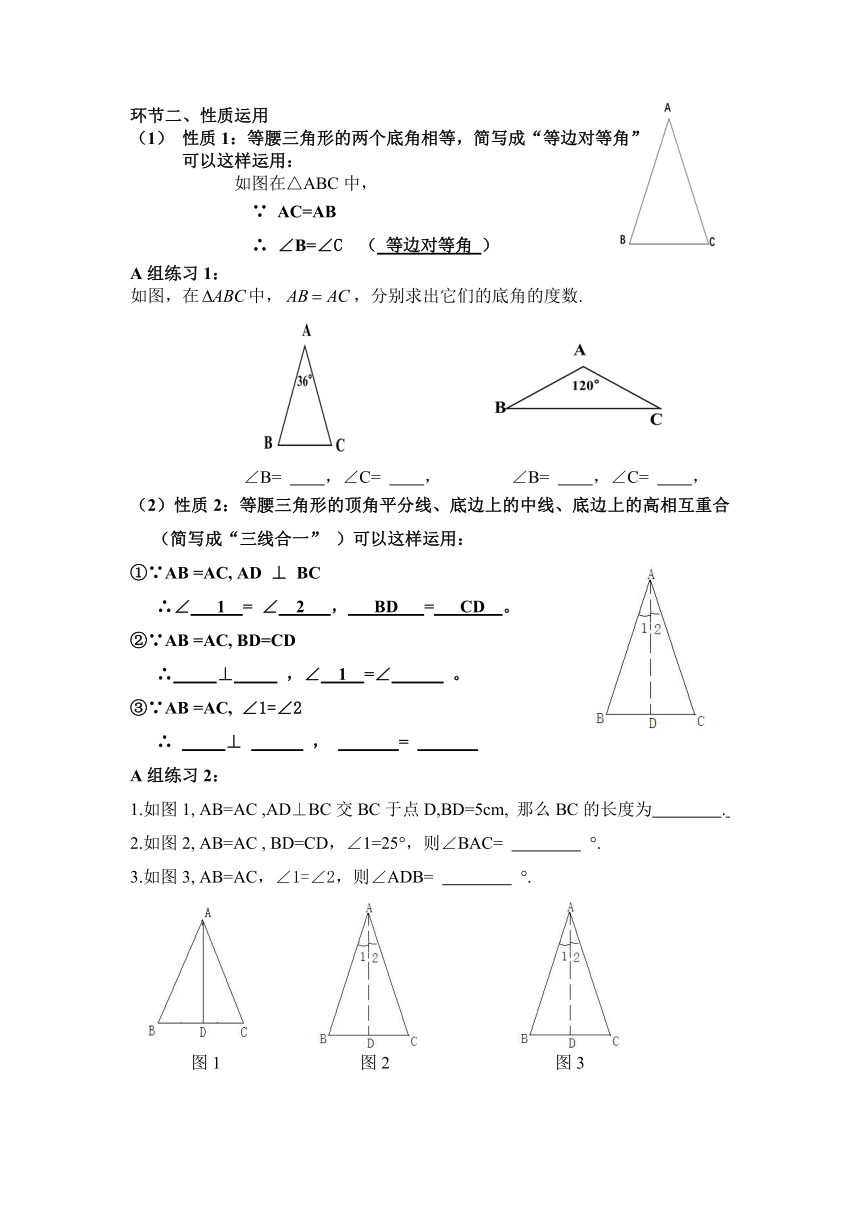
性质1:等腰三角形的两个底角相等,简写成“等边对等角”
可以这样运用:
如图在△ABC中,
∵
AC=AB
∴
∠B=∠C
(
等边对等角
)
A组练习1:
如图,在中,,分别求出它们的底角的度数.
∠B=
,∠C=
,
∠B=
,∠C=
,
(2)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”
)可以这样运用:
①∵AB
=AC,
AD
⊥
BC
∴∠
1
=
∠
2
,
BD
=
CD
。
②∵AB
=AC,
BD=CD
∴
⊥
,∠
1
=∠
。
③∵AB
=AC,
∠1=∠2
∴
⊥
,
=
A组练习2:
1.如图1,
AB=AC
,AD⊥BC交
( http: / / www.21cnjy.com )BC于点D,BD=5cm,
那么BC的长度为
.
2.如图2,
AB=AC
,
BD=CD,∠1=25°,则∠BAC=
°.
3.如图3,
AB=AC,∠1=∠2,则∠ADB=
°.
图1
图2
图3
环节三、例题讲解
如图,在中,,点D在AC上,且BD=BC=AD
(1)若∠A=36°则∠1=
°,∠2
=
°
(2)若∠A=X,则∠2
=
(3)根据题目条件直接求出各角的度数
环节四、巩固练习
(B组练习)
1.
(课本第77页练习2)如图△ABC是
( http: / / www.21cnjy.com )等腰直角三角形AB=AC,∠BAC=90°,AD是底边BC上的高,则∠B=
°,
∠C=
°,
∠BAD=
°,
∠DAC=
°
2.等腰三角形的一个角是110°,它的另外两个角的度数是
.
3.等腰三角形的一个角是80°,它的另外两个角的度数是
.
4.如图,,,求证:平分
证明:
(C组练习)
4.(课本第77页练习3)在中,,∠BAD=26°,
求和的度数
解:
环节五、小结:
性质1:等腰三角形的两个底角
。简称(“
”
)
性质2:等腰三角形的
与
,
互相重合
(简写成“
”
)
性质3:等腰三角形
(填“是”或“不是”)轴对称图形,其对称轴是
环节六.作业布置:
阳光学业评价第73页基础训练1—7题.
班别
学号
姓名
一、学习目标
1、掌握等腰三角形的概念,等腰三角形的性质.
2、会运用性质,会进行简单的说理.
二、前置作业:
(1)如图12.3-1拿出一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它打开,得到的三角形ABC有什么特点?请在图形上标上字母.
(2)如上图,把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,
填入下表:
重合的线段
重合的角
(3)预习:阅读课本第76页。根据所剪三角形和前置作业(2),你能发现等腰三角形的性质吗?
性质1、
性质2:
性质3:等腰三角形
(填“是”或“不是”
)轴对称图形,
其对称轴是
三、新课学习:
环节一、性质证明
已知:△ABC中,AB=AC
,求证:∠B=C
环节二、性质运用
性质1:等腰三角形的两个底角相等,简写成“等边对等角”
可以这样运用:
如图在△ABC中,
∵
AC=AB
∴
∠B=∠C
(
等边对等角
)
A组练习1:
如图,在中,,分别求出它们的底角的度数.
∠B=
,∠C=
,
∠B=
,∠C=
,
(2)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”
)可以这样运用:
①∵AB
=AC,
AD
⊥
BC
∴∠
1
=
∠
2
,
BD
=
CD
。
②∵AB
=AC,
BD=CD
∴
⊥
,∠
1
=∠
。
③∵AB
=AC,
∠1=∠2
∴
⊥
,
=
A组练习2:
1.如图1,
AB=AC
,AD⊥BC交
( http: / / www.21cnjy.com )BC于点D,BD=5cm,
那么BC的长度为
.
2.如图2,
AB=AC
,
BD=CD,∠1=25°,则∠BAC=
°.
3.如图3,
AB=AC,∠1=∠2,则∠ADB=
°.
图1
图2
图3
环节三、例题讲解
如图,在中,,点D在AC上,且BD=BC=AD
(1)若∠A=36°则∠1=
°,∠2
=
°
(2)若∠A=X,则∠2
=
(3)根据题目条件直接求出各角的度数
环节四、巩固练习
(B组练习)
1.
(课本第77页练习2)如图△ABC是
( http: / / www.21cnjy.com )等腰直角三角形AB=AC,∠BAC=90°,AD是底边BC上的高,则∠B=
°,
∠C=
°,
∠BAD=
°,
∠DAC=
°
2.等腰三角形的一个角是110°,它的另外两个角的度数是
.
3.等腰三角形的一个角是80°,它的另外两个角的度数是
.
4.如图,,,求证:平分
证明:
(C组练习)
4.(课本第77页练习3)在中,,∠BAD=26°,
求和的度数
解:
环节五、小结:
性质1:等腰三角形的两个底角
。简称(“
”
)
性质2:等腰三角形的
与
,
互相重合
(简写成“
”
)
性质3:等腰三角形
(填“是”或“不是”)轴对称图形,其对称轴是
环节六.作业布置:
阳光学业评价第73页基础训练1—7题.
