天津南开区2017年3月八年级下矩形的性质与判定周测题(含答案)
文档属性
| 名称 | 天津南开区2017年3月八年级下矩形的性质与判定周测题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 441.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-03-28 00:00:00 | ||
图片预览

文档简介
八年级数学
下册
矩形的性质与判定
周练习题
、选择题:
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为(
)
A.4
B.8
C.10
D.12
下列三个命题中,是真命题的有(
)
①对角线相等的四边形是矩形;
②三个角是直角的四边形是矩形;
③有一个角是直角的平行四边形是矩形.
A.3个
B.2个
C.1个
D.0个
如图,矩形ABCD两条对角线相交于点O,∠AOB=60°,AB=2,则矩形对角线AC长是(
)
A.2
B.4
C.
D.
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是(
)
A.△AFD≌△DCE
B.AF=AD
C.AB=AF
D.BE=AD﹣DF
如图,平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于(
)
A.20°
B.25°
C.30°
D.35°
如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是(
)
A.△EBD是等腰三角形,EB=ED
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
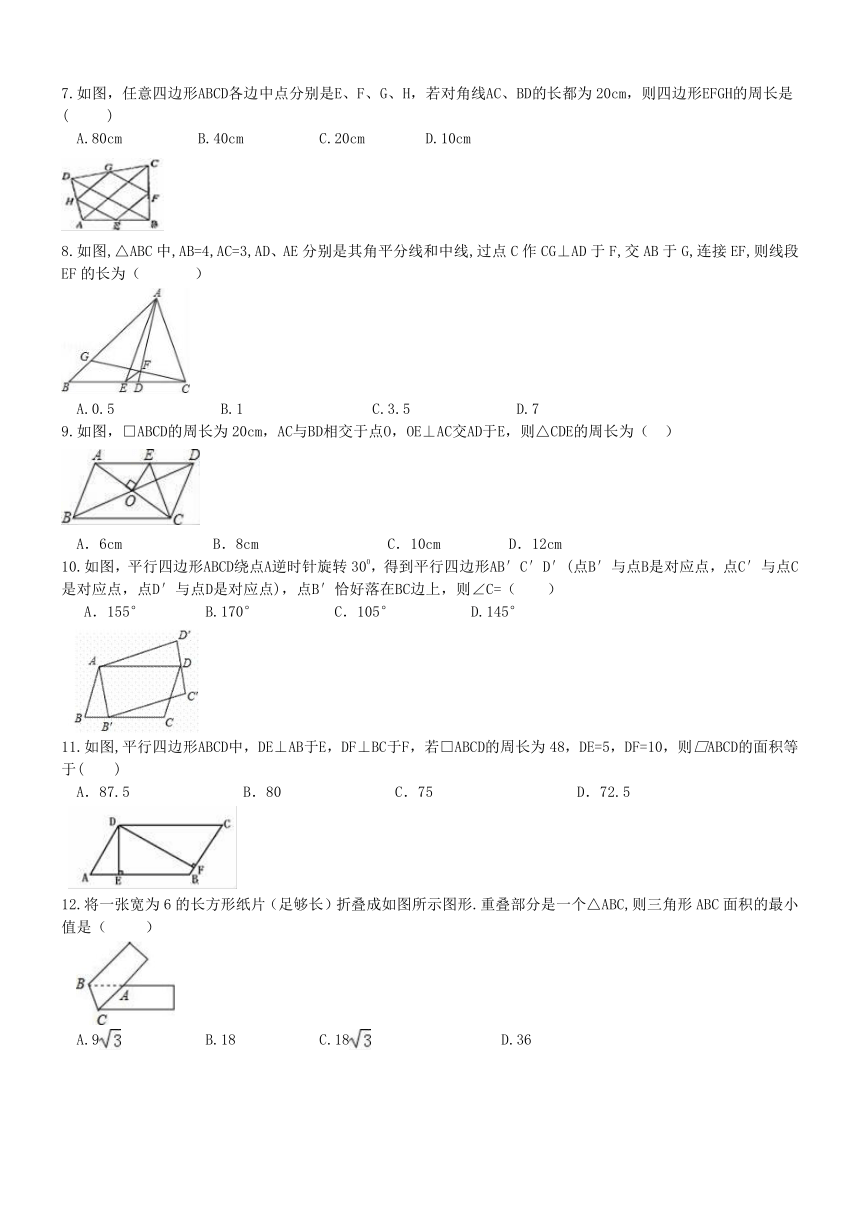
如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为20cm,则四边形EFGH的周长是
(
)
A.80cm
B.40cm
C.20cm
D.10cm
如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为(
)
A.0.5
B.1
C.3.5
D.7
如图,□ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为(
)
A.6cm
B.8cm
C.10cm
D.12cm
如图,平行四边形ABCD绕点A逆时针旋转300,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=(
)
A.155°
B.170°
C.105°
D.145°
如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若□ABCD的周长为48,DE=5,DF=10,则□ABCD的面积等于(
)
A.87.5
B.80
C.75
D.72.5
将一张宽为6的长方形纸片(足够长)折叠成如图所示图形.重叠部分是一个△ABC,则三角形ABC面积的最小值是(
)
A.9
B.18
C.18
D.36
、填空题:
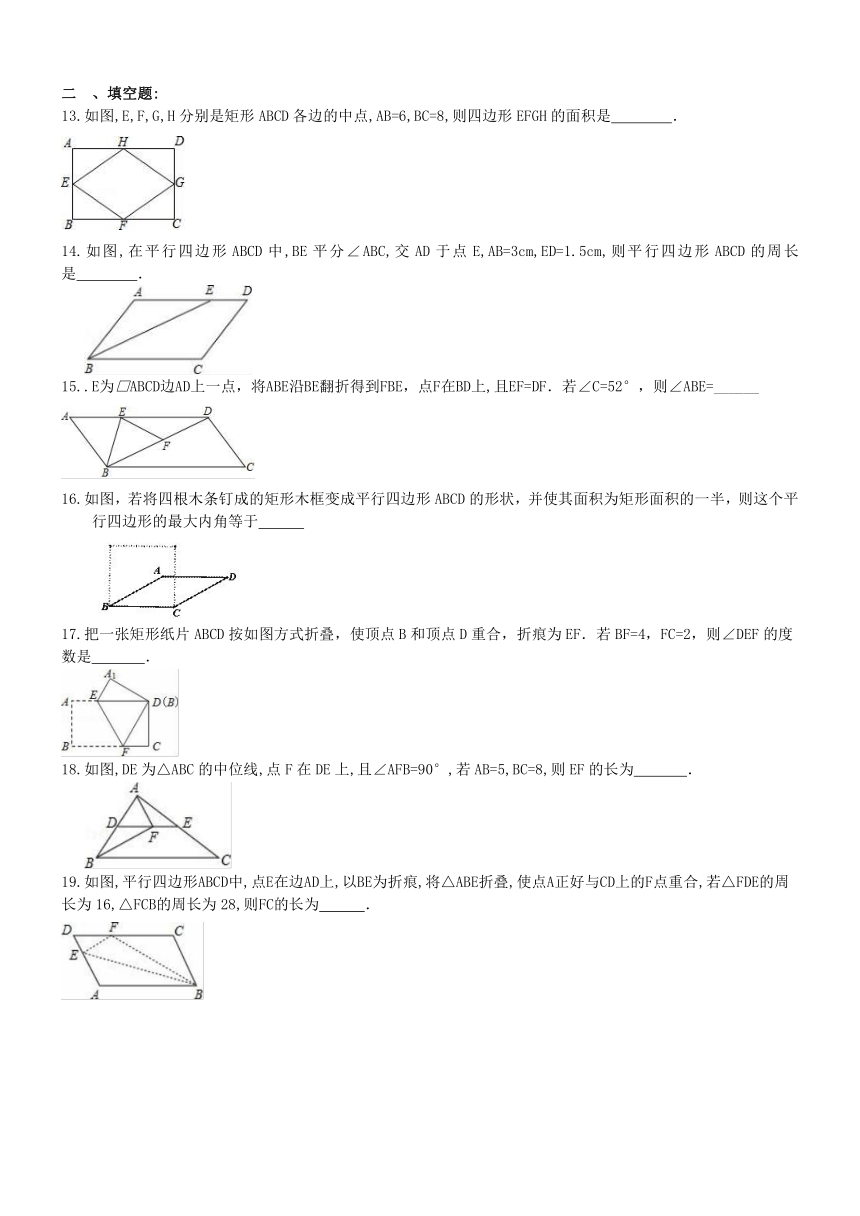
如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是
.
如图,在平行四边形ABCD中,BE平分∠ABC,交AD于点E,AB=3cm,ED=1.5cm,则平行四边形ABCD的周长是
.
.E为□ABCD边AD上一点,将ABE沿BE翻折得到FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE=______
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最大内角等于
把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若BF=4,FC=2,则∠DEF的度数是
.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为
.
如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为
.
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为
.
、解答题:
如图,□ABCD的对角线相交于点O,EF过点O分别与AD,BC相交于点E,F.
(1)求证:△AOE≌△COF;
(2)若AB=4,BC=7,OE=3,试求四边形EFCD的周长.
如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若AB=4,点F为DC的中点,DG⊥AE,垂足为G,且DG=1,求AE的长.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
参考答案
1.B
2.B
3.B
4.B
5.A
6.B
7.B
8.A
9.C
10.A
11.B
12.B
13.答案为:24.
14.答案为:15cm.
15.51
16.150°
17.答案为:60.
18.答案为:1.5.
19.答案为:6.
20.【解答】解:①当DF=DO时,在RT△AOD中,∵AO=3,AD=4,
∴OD=5,∴CD=DF=DO=5,∴点C坐标(8,4).②OD=OF时,∵DF=OD=5,OA=3,
∴AF=2,DF=CD=2,∴点C坐标(3+2,4).
③当FD=FO时,设FD=FO=x,在RT△ADF中,∵AD2+AF2=DF2,
∴42+(x﹣3)2=x2,∴x=,∴点C坐标(,4).
综上所述,满足条件的点C坐标(8,4)或(3+2,4)或(,4).
故答案为(8,4)或(3+2,4)或(,4).
21.(1)证明:∵AD∥BC,∴∠EAO=∠FCO.
又∵∠AOE=∠COF,OA=OC,
在△AOE和△COF中,,∴△AOE≌△COF.
(2)∵△AOE≌△COF∴AE=FC,OF=OE
又∵在ABCD中,BC=AD
CD=AB∴FC+DE=AE+ED=AD=BC=7
∴S四边形EFCD=EF+FC+CD+ED=6+7+4=17
22.【解答】(1)证明:∵四边形ABCD是矩形,∴AD=BC,∠D=∠BCD=90°.
∴∠BCF=180°﹣∠BCD=180°﹣90°=90°.
∴∠D=∠BCF.在Rt△ADE和Rt△BCF中,∴Rt△ADE≌Rt△BCF.
∴∠1=∠F.∴AE∥BF.∵AE=BF,∴四边形ABFE是平行四边形.
(2)解:∵∠D=90°,∴∠DAE+∠1=90°.
∵∠BEF=∠DAE,∴∠BEF+∠1=90°.
∵∠BEF+∠1+∠AEB=180°,∴∠AEB=90°.
在Rt△ABE中,AE=3,BE=4,AB=.
∵四边形ABFE是平行四边形,∴EF=AB=5.
23.【解答】(1)证明:∵AE为∠ADB的平分线,∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB.
∴∠DAE=∠E.∴∠BAE=∠E.∴AB=BE.∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,∴CD∥AB,
∴∠BAF=∠DFA.∴∠DAF=∠DFA.∴DA=DF.
∵F为DC的中点,AB=4,∴DF=CF=DA=2.
∵DG⊥AE,DG=1,∴AG=GF.∴AG=.∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).∴AF=EF,∴AE=2AF=4.
24.【解答】:(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,∴∠1=∠5,∠3=∠6,∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,∴EF==10,∴OC=EF=5;
(3)答:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,∴四边形AECF是平行四边形,
∵∠ECF=90°,∴平行四边形AECF是矩形.
下册
矩形的性质与判定
周练习题
、选择题:
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为(
)
A.4
B.8
C.10
D.12
下列三个命题中,是真命题的有(
)
①对角线相等的四边形是矩形;
②三个角是直角的四边形是矩形;
③有一个角是直角的平行四边形是矩形.
A.3个
B.2个
C.1个
D.0个
如图,矩形ABCD两条对角线相交于点O,∠AOB=60°,AB=2,则矩形对角线AC长是(
)
A.2
B.4
C.
D.
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是(
)
A.△AFD≌△DCE
B.AF=AD
C.AB=AF
D.BE=AD﹣DF
如图,平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于(
)
A.20°
B.25°
C.30°
D.35°
如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是(
)
A.△EBD是等腰三角形,EB=ED
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
如图,任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC、BD的长都为20cm,则四边形EFGH的周长是
(
)
A.80cm
B.40cm
C.20cm
D.10cm
如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为(
)
A.0.5
B.1
C.3.5
D.7
如图,□ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为(
)
A.6cm
B.8cm
C.10cm
D.12cm
如图,平行四边形ABCD绕点A逆时针旋转300,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=(
)
A.155°
B.170°
C.105°
D.145°
如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若□ABCD的周长为48,DE=5,DF=10,则□ABCD的面积等于(
)
A.87.5
B.80
C.75
D.72.5
将一张宽为6的长方形纸片(足够长)折叠成如图所示图形.重叠部分是一个△ABC,则三角形ABC面积的最小值是(
)
A.9
B.18
C.18
D.36
、填空题:
如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是
.
如图,在平行四边形ABCD中,BE平分∠ABC,交AD于点E,AB=3cm,ED=1.5cm,则平行四边形ABCD的周长是
.
.E为□ABCD边AD上一点,将ABE沿BE翻折得到FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE=______
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最大内角等于
把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若BF=4,FC=2,则∠DEF的度数是
.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为
.
如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为
.
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为
.
、解答题:
如图,□ABCD的对角线相交于点O,EF过点O分别与AD,BC相交于点E,F.
(1)求证:△AOE≌△COF;
(2)若AB=4,BC=7,OE=3,试求四边形EFCD的周长.
如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若AB=4,点F为DC的中点,DG⊥AE,垂足为G,且DG=1,求AE的长.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
参考答案
1.B
2.B
3.B
4.B
5.A
6.B
7.B
8.A
9.C
10.A
11.B
12.B
13.答案为:24.
14.答案为:15cm.
15.51
16.150°
17.答案为:60.
18.答案为:1.5.
19.答案为:6.
20.【解答】解:①当DF=DO时,在RT△AOD中,∵AO=3,AD=4,
∴OD=5,∴CD=DF=DO=5,∴点C坐标(8,4).②OD=OF时,∵DF=OD=5,OA=3,
∴AF=2,DF=CD=2,∴点C坐标(3+2,4).
③当FD=FO时,设FD=FO=x,在RT△ADF中,∵AD2+AF2=DF2,
∴42+(x﹣3)2=x2,∴x=,∴点C坐标(,4).
综上所述,满足条件的点C坐标(8,4)或(3+2,4)或(,4).
故答案为(8,4)或(3+2,4)或(,4).
21.(1)证明:∵AD∥BC,∴∠EAO=∠FCO.
又∵∠AOE=∠COF,OA=OC,
在△AOE和△COF中,,∴△AOE≌△COF.
(2)∵△AOE≌△COF∴AE=FC,OF=OE
又∵在ABCD中,BC=AD
CD=AB∴FC+DE=AE+ED=AD=BC=7
∴S四边形EFCD=EF+FC+CD+ED=6+7+4=17
22.【解答】(1)证明:∵四边形ABCD是矩形,∴AD=BC,∠D=∠BCD=90°.
∴∠BCF=180°﹣∠BCD=180°﹣90°=90°.
∴∠D=∠BCF.在Rt△ADE和Rt△BCF中,∴Rt△ADE≌Rt△BCF.
∴∠1=∠F.∴AE∥BF.∵AE=BF,∴四边形ABFE是平行四边形.
(2)解:∵∠D=90°,∴∠DAE+∠1=90°.
∵∠BEF=∠DAE,∴∠BEF+∠1=90°.
∵∠BEF+∠1+∠AEB=180°,∴∠AEB=90°.
在Rt△ABE中,AE=3,BE=4,AB=.
∵四边形ABFE是平行四边形,∴EF=AB=5.
23.【解答】(1)证明:∵AE为∠ADB的平分线,∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB.
∴∠DAE=∠E.∴∠BAE=∠E.∴AB=BE.∴CD=BE.
(2)解:∵四边形ABCD是平行四边形,∴CD∥AB,
∴∠BAF=∠DFA.∴∠DAF=∠DFA.∴DA=DF.
∵F为DC的中点,AB=4,∴DF=CF=DA=2.
∵DG⊥AE,DG=1,∴AG=GF.∴AG=.∴AF=2AG=2.
在△ADF和△ECF中,,
∴△ADF≌△ECF(AAS).∴AF=EF,∴AE=2AF=4.
24.【解答】:(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,∴∠1=∠5,∠3=∠6,∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,∴EF==10,∴OC=EF=5;
(3)答:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,∴四边形AECF是平行四边形,
∵∠ECF=90°,∴平行四边形AECF是矩形.
