17.2 勾股定理的逆定理(带解析)
图片预览


文档简介
17.2 勾股定理的逆定理(带解析)
一、选择题
1.以下列各组数作为三角形的边长,其中不能构成直角三角形的是( )
A.6,8,10 B.5,12,13 C.9,40,41 D.5,6,7
2.已知△ABC的三边长分别是3cm、4cm、5cm,则△ABC的面积是( )
A.6cm2 B.7.5cm2 C.10cm2 D.12cm2
3.已知△ABC的边为a、b、c,且(a+b+c)(a+b-c)=2ab,则这个三角形是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
4.已知二条线段的长分别为cm,cm,那么能与它们组成直角三角形的第三条线段的长是( )
A.1cm B.cm C.5cm D.1cm与cm
5.一个三角形如果有两边的垂直平分线的交点在第三边上,那么这个三角形是( ) A.等腰三角形 B.等边三角形www.21-cn-jy.com
C.直角三角形 D.等腰直角三角形
6.一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )21·cn·jy·com
A.10米 B.15米 C.25米 D.30米
7.如图,小红从A地向北偏东30°,方向走100米到B地,再从B地向西走200米到C地,这时小红距A地( )2·1·c·n·j·y
A.150米 B.100米 C.100米 D.50米
二、填空题
8.以下列各组数为边长:①3、4、5;②5,12,13;③3,5,7;④9,40,41;⑤10,12,13;其中能构成直角三角形的有??? .21教育网
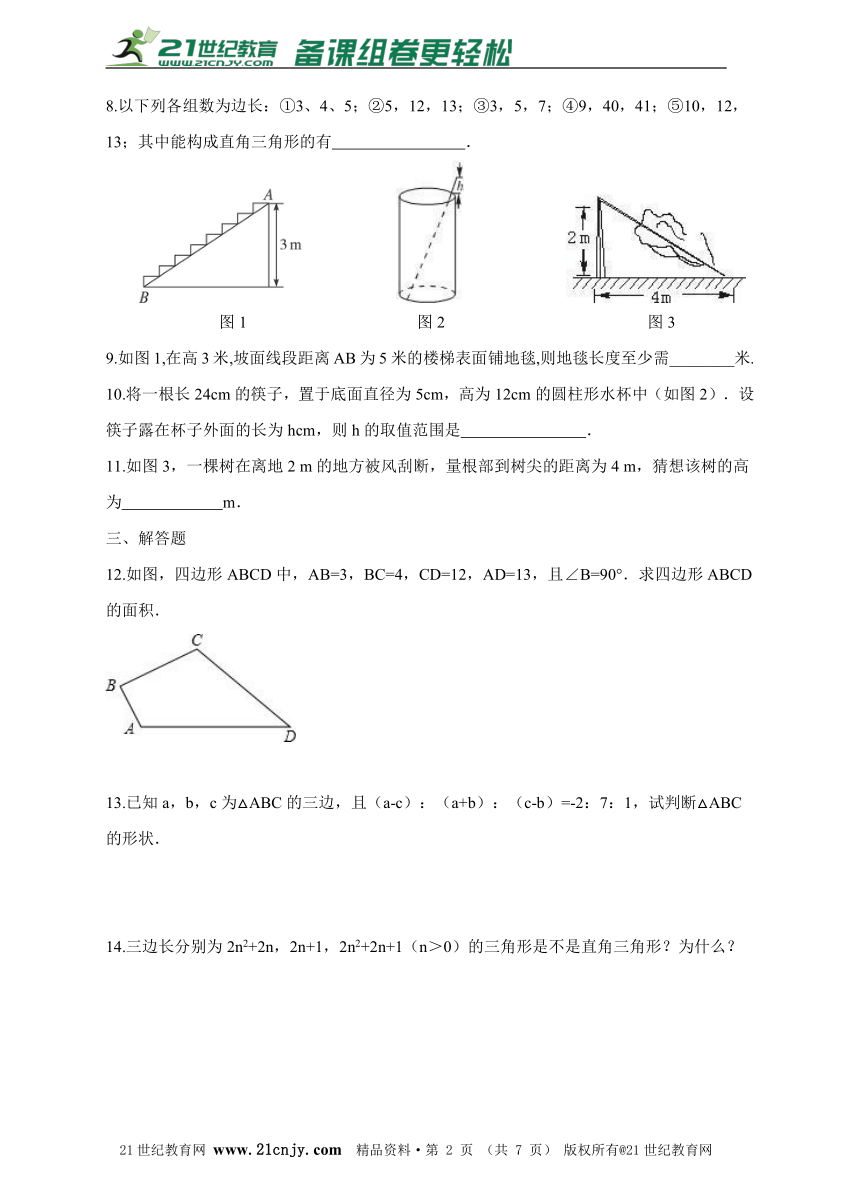
图1 图2 图3
9.如图1,在高3米,坡面线段距离AB为5米的楼梯表面铺地毯,则地毯长度至少需________米.
10.将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中(如图2).设筷子露在杯子外面的长为hcm,则h的取值范围是??? .
11.如图3,一棵树在离地2?m的地方被风刮断,量根部到树尖的距离为4?m,猜想该树的高为??? m.【来源:21·世纪·教育·网】
三、解答题
12.如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD的面积.21*cnjy*com
13.已知a,b,c为△ABC的三边,且(a-c):(a+b):(c-b)=-2:7:1,试判断△ABC的形状.21·世纪*教育网
14.三边长分别为2n2+2n,2n+1,2n2+2n+1(n>0)的三角形是不是直角三角形?为什么?
参考答案及解析
1.D
【解析】A、能,∵62+82=102=100,∴能构成直角三角形; B、能,52+122=132=169,∴能构成直角三角形; C、能,92+402=412=1681,∴能构成直角三角形; 21世纪教育网版权所有
5.C
【解析】如图,CA、CB的中点分别为D、E,CA、CB的垂直平分线OD、OE相交于点O,且点O落在AB边上,21cnjy.com
连接CO, ∵OD是AC的垂直平分线, ∴OC=OA, 同理OC=OB, ∴OA=OB=OC, ∴A、B、C都落在以O为圆心,以AB为直径的圆周上, ∴C是直角. 6.Bwww-2-1-cnjy-com
【解析】如图
在Rt△ABC中,∵∠ABC=30°, ∴AB=2AC, 而CA=5米, ∴AB=10米,
∵DA=50, ∴勾股定理得,AC=100. 8.①②④ 【解析】①32+42=52,②52+122=132,③32+52≠72,④92+402=412,⑤102+122≠132; 所以①②④组数为边长的能构成直角三角形, 9.72-1-c-n-j-y
【解析】由勾股定理求出另一直角边为4,将楼梯表面向下和右平移,则地毯的总长=两直角边的和=3+4=7.【来源:21cnj*y.co*m】
10.11≤h≤12.
【解析】
首先根据圆柱的高,知筷子在杯内的最小长度是12cm,则在杯外的最大长度是24-12=12; 再根据勾股定理求得筷子在杯内的最大长度是(如图)AC===13,则在杯外的最小长度是24-13=11cm. 所以h的取值范围是11≤h≤12. 11.+2 【解析】∵在直角三角形中,
∵(a-c):(c-b)=-2:1 ∴a-2b+c=0 ② ∵(a+b):(c-b)=7:1 ∴a+8b-7c=0 ③ ∵①+②得a:c=3:5,①-③得a:b=3:4 ∴a:b:c=3:4:5 ∴△ABC是直角三角形 14.三边长为2n2+2n,2n+1,2n2+2n+1(n>0)的三角形是直角三角形 【解析】证明:∵三边长为2n2+2n,2n+1,2n2+2n+1(n>0), ∴(2n2+2n)2=4n4+8n3+4n2, (2n+1)2=4n2+4n+1, (2n2+2n+1)2=4n4+4n2+1+8n3+4n2+4n=4n4+8n3+8n2+4n+1, ∴(2n2+2n)2+(2n+1)2=4n4+8n3+8n2+4n+1, ∴(2n2+2n)2+(2n+1)2=(2n2+2n+1)2, 故三边长为2n2+2n,2n+1,2n2+2n+1(n>0)的三角形是直角三角形.
一、选择题
1.以下列各组数作为三角形的边长,其中不能构成直角三角形的是( )
A.6,8,10 B.5,12,13 C.9,40,41 D.5,6,7
2.已知△ABC的三边长分别是3cm、4cm、5cm,则△ABC的面积是( )
A.6cm2 B.7.5cm2 C.10cm2 D.12cm2
3.已知△ABC的边为a、b、c,且(a+b+c)(a+b-c)=2ab,则这个三角形是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
4.已知二条线段的长分别为cm,cm,那么能与它们组成直角三角形的第三条线段的长是( )
A.1cm B.cm C.5cm D.1cm与cm
5.一个三角形如果有两边的垂直平分线的交点在第三边上,那么这个三角形是( ) A.等腰三角形 B.等边三角形www.21-cn-jy.com
C.直角三角形 D.等腰直角三角形
6.一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )21·cn·jy·com
A.10米 B.15米 C.25米 D.30米
7.如图,小红从A地向北偏东30°,方向走100米到B地,再从B地向西走200米到C地,这时小红距A地( )2·1·c·n·j·y
A.150米 B.100米 C.100米 D.50米
二、填空题
8.以下列各组数为边长:①3、4、5;②5,12,13;③3,5,7;④9,40,41;⑤10,12,13;其中能构成直角三角形的有??? .21教育网
图1 图2 图3
9.如图1,在高3米,坡面线段距离AB为5米的楼梯表面铺地毯,则地毯长度至少需________米.
10.将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中(如图2).设筷子露在杯子外面的长为hcm,则h的取值范围是??? .
11.如图3,一棵树在离地2?m的地方被风刮断,量根部到树尖的距离为4?m,猜想该树的高为??? m.【来源:21·世纪·教育·网】
三、解答题
12.如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且∠B=90°.求四边形ABCD的面积.21*cnjy*com
13.已知a,b,c为△ABC的三边,且(a-c):(a+b):(c-b)=-2:7:1,试判断△ABC的形状.21·世纪*教育网
14.三边长分别为2n2+2n,2n+1,2n2+2n+1(n>0)的三角形是不是直角三角形?为什么?
参考答案及解析
1.D
【解析】A、能,∵62+82=102=100,∴能构成直角三角形; B、能,52+122=132=169,∴能构成直角三角形; C、能,92+402=412=1681,∴能构成直角三角形; 21世纪教育网版权所有
5.C
【解析】如图,CA、CB的中点分别为D、E,CA、CB的垂直平分线OD、OE相交于点O,且点O落在AB边上,21cnjy.com
连接CO, ∵OD是AC的垂直平分线, ∴OC=OA, 同理OC=OB, ∴OA=OB=OC, ∴A、B、C都落在以O为圆心,以AB为直径的圆周上, ∴C是直角. 6.Bwww-2-1-cnjy-com
【解析】如图
在Rt△ABC中,∵∠ABC=30°, ∴AB=2AC, 而CA=5米, ∴AB=10米,
∵DA=50, ∴勾股定理得,AC=100. 8.①②④ 【解析】①32+42=52,②52+122=132,③32+52≠72,④92+402=412,⑤102+122≠132; 所以①②④组数为边长的能构成直角三角形, 9.72-1-c-n-j-y
【解析】由勾股定理求出另一直角边为4,将楼梯表面向下和右平移,则地毯的总长=两直角边的和=3+4=7.【来源:21cnj*y.co*m】
10.11≤h≤12.
【解析】
首先根据圆柱的高,知筷子在杯内的最小长度是12cm,则在杯外的最大长度是24-12=12; 再根据勾股定理求得筷子在杯内的最大长度是(如图)AC===13,则在杯外的最小长度是24-13=11cm. 所以h的取值范围是11≤h≤12. 11.+2 【解析】∵在直角三角形中,
∵(a-c):(c-b)=-2:1 ∴a-2b+c=0 ② ∵(a+b):(c-b)=7:1 ∴a+8b-7c=0 ③ ∵①+②得a:c=3:5,①-③得a:b=3:4 ∴a:b:c=3:4:5 ∴△ABC是直角三角形 14.三边长为2n2+2n,2n+1,2n2+2n+1(n>0)的三角形是直角三角形 【解析】证明:∵三边长为2n2+2n,2n+1,2n2+2n+1(n>0), ∴(2n2+2n)2=4n4+8n3+4n2, (2n+1)2=4n2+4n+1, (2n2+2n+1)2=4n4+4n2+1+8n3+4n2+4n=4n4+8n3+8n2+4n+1, ∴(2n2+2n)2+(2n+1)2=4n4+8n3+8n2+4n+1, ∴(2n2+2n)2+(2n+1)2=(2n2+2n+1)2, 故三边长为2n2+2n,2n+1,2n2+2n+1(n>0)的三角形是直角三角形.
