1.1 直角三角形的性质和判定(Ⅰ) 课件
文档属性
| 名称 | 1.1 直角三角形的性质和判定(Ⅰ) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-28 00:00:00 | ||
图片预览






文档简介
课件15张PPT。1.1 直角三角形的性质和判定(Ⅰ)一、想一想,探求判定定理 1.如图在Rt△ABC中,
两锐角的和∠A+∠ B=? 2.如图在△ABC中,
如果∠A+∠ B=90 °,△ABC是直角三角形吗? 定理:有两个角互余的三角形是直角三角形.二、做一做,感受性质定理三、想一想,探究性质定理 如图,在Rt△ABC中,∠C=90°,如果中线为CD,是否有CD= AB,为什么?试说明理由.(D′)过C作射线CD′交AB于D′,使∠ 1=∠ A,
则AD′=CD′(等角对等边)
又∠A+∠B=90°(直角三角形两锐角互余)
∠C=∠1+∠2=90°
∴∠B=∠2
于是BD′=CD′(等角对等边)
故BD′=AD′=CD′
∴ D′为AB中点(线段中点定义)
∵D为AB中点(三角形中线的定义)
∴D与D′重合
因此CD=CD′= AB
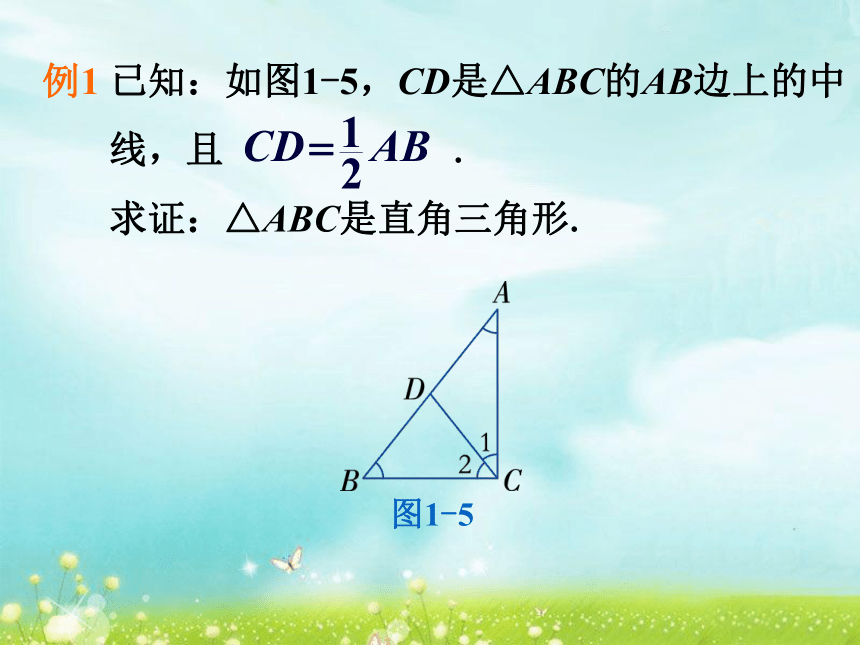
定理:直角三角形中,斜边上的中线等于斜边的一半.四、范例分析,巩固定理如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形吗?图1-5根据三角形内角和性质,有
∠A+∠B+∠ACB =180°,
即得∠A+∠B+∠1+∠2=180°,
2(∠A+∠B)=180°.所以 ∠A+∠B =90°.根据直角三角形判定定理,所以△ABC是直角三角形. 如图,在Rt△ABC中,∠BCA=90°,
如果∠A=30°,那么直角边BC与斜边AB
有什么关系呢?五、开动脑筋,应用探索如图,取线段AB的中点D,连接CD.∴ △BDC为等边三角形. ∴ ∠B=60°.∵ CD是Rt△ABC斜边AB上的中线,∴∵ ∠BCA=90°,且∠A=30°,∴在直角三角形中,如
果一个锐角等于30°,那么它所对的直角边等于斜边的一半.如图1-8所示,在A岛周围20海里(1海里=1852m) 水域内有暗礁,一轮船由西向东航行到O处时,
发现A岛在北偏东60°的方向,且与轮船相距
海里,若该船继续保持航向不变,有触暗礁的
危险吗?图1-8例2 解 轮船在航行过程中,
如果与A岛的距离始终大于20海里,
则轮船就不会触暗礁.在图1-8中,过A点作AD⊥OB,垂足为D,连接AO.B图1-8所以轮船不会触礁.(海里)1.如图,AB ⊥DB,CD ⊥DB,下列说法错误的是( )A.一定有∠A=∠CB.只要有一边相等就有△ABO≌ △CDOC.只要再给一个条件就能得到△ABO≌ △CDOD.有OA=OC或OB=OD,就有AB=CD等腰直角三角形C20°40°120°七、小结1.直角三角形的两个锐角互余.2.有两个角互余的三角形是直角三角形.3.直角三角形斜边上的中线等于斜边的一半.4.直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.再 见
两锐角的和∠A+∠ B=? 2.如图在△ABC中,
如果∠A+∠ B=90 °,△ABC是直角三角形吗? 定理:有两个角互余的三角形是直角三角形.二、做一做,感受性质定理三、想一想,探究性质定理 如图,在Rt△ABC中,∠C=90°,如果中线为CD,是否有CD= AB,为什么?试说明理由.(D′)过C作射线CD′交AB于D′,使∠ 1=∠ A,
则AD′=CD′(等角对等边)
又∠A+∠B=90°(直角三角形两锐角互余)
∠C=∠1+∠2=90°
∴∠B=∠2
于是BD′=CD′(等角对等边)
故BD′=AD′=CD′
∴ D′为AB中点(线段中点定义)
∵D为AB中点(三角形中线的定义)
∴D与D′重合
因此CD=CD′= AB
定理:直角三角形中,斜边上的中线等于斜边的一半.四、范例分析,巩固定理如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形吗?图1-5根据三角形内角和性质,有
∠A+∠B+∠ACB =180°,
即得∠A+∠B+∠1+∠2=180°,
2(∠A+∠B)=180°.所以 ∠A+∠B =90°.根据直角三角形判定定理,所以△ABC是直角三角形. 如图,在Rt△ABC中,∠BCA=90°,
如果∠A=30°,那么直角边BC与斜边AB
有什么关系呢?五、开动脑筋,应用探索如图,取线段AB的中点D,连接CD.∴ △BDC为等边三角形. ∴ ∠B=60°.∵ CD是Rt△ABC斜边AB上的中线,∴∵ ∠BCA=90°,且∠A=30°,∴在直角三角形中,如
果一个锐角等于30°,那么它所对的直角边等于斜边的一半.如图1-8所示,在A岛周围20海里(1海里=1852m) 水域内有暗礁,一轮船由西向东航行到O处时,
发现A岛在北偏东60°的方向,且与轮船相距
海里,若该船继续保持航向不变,有触暗礁的
危险吗?图1-8例2 解 轮船在航行过程中,
如果与A岛的距离始终大于20海里,
则轮船就不会触暗礁.在图1-8中,过A点作AD⊥OB,垂足为D,连接AO.B图1-8所以轮船不会触礁.(海里)1.如图,AB ⊥DB,CD ⊥DB,下列说法错误的是( )A.一定有∠A=∠CB.只要有一边相等就有△ABO≌ △CDOC.只要再给一个条件就能得到△ABO≌ △CDOD.有OA=OC或OB=OD,就有AB=CD等腰直角三角形C20°40°120°七、小结1.直角三角形的两个锐角互余.2.有两个角互余的三角形是直角三角形.3.直角三角形斜边上的中线等于斜边的一半.4.直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.再 见
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
