1.2 直角三角形的性质和判定(Ⅱ) 课件
文档属性
| 名称 | 1.2 直角三角形的性质和判定(Ⅱ) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 270.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-28 00:00:00 | ||
图片预览









文档简介
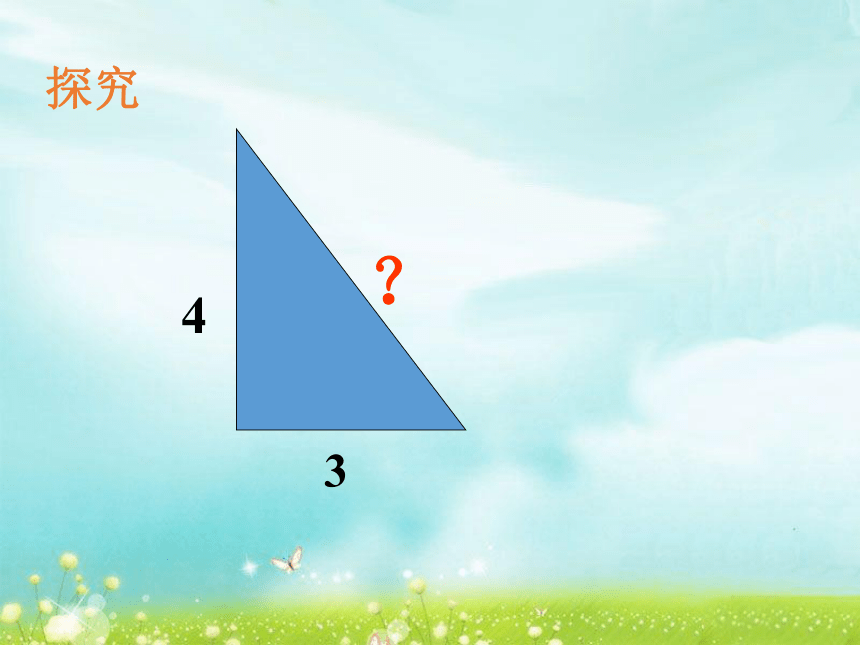
课件31张PPT。1.2 直角三角形的性质和判定(Ⅱ) 34?探究弦勾 股 弦
3 4 5
6 8 10
5 12 13
……勾2+股2=弦2勾股勾股定理
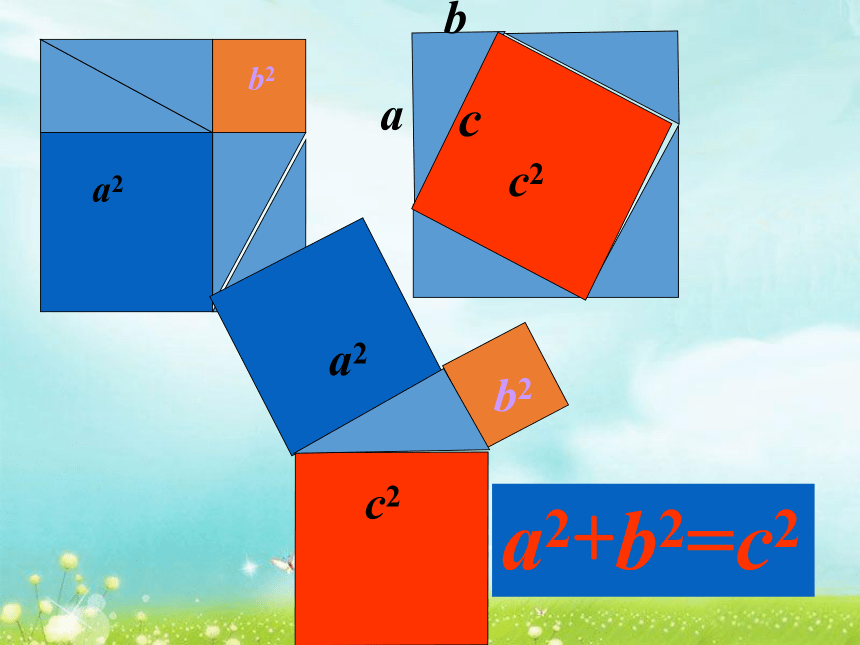
直角三角形两直角边a、b的平方和,等于斜边c的平方. 即a2+b2=c2面积证法(面积割补法) 图形面积的有关性质:
(1)两个图形全等,它们的面积相等;
(2)一个图形的面积,等于它的各部分面积的和.
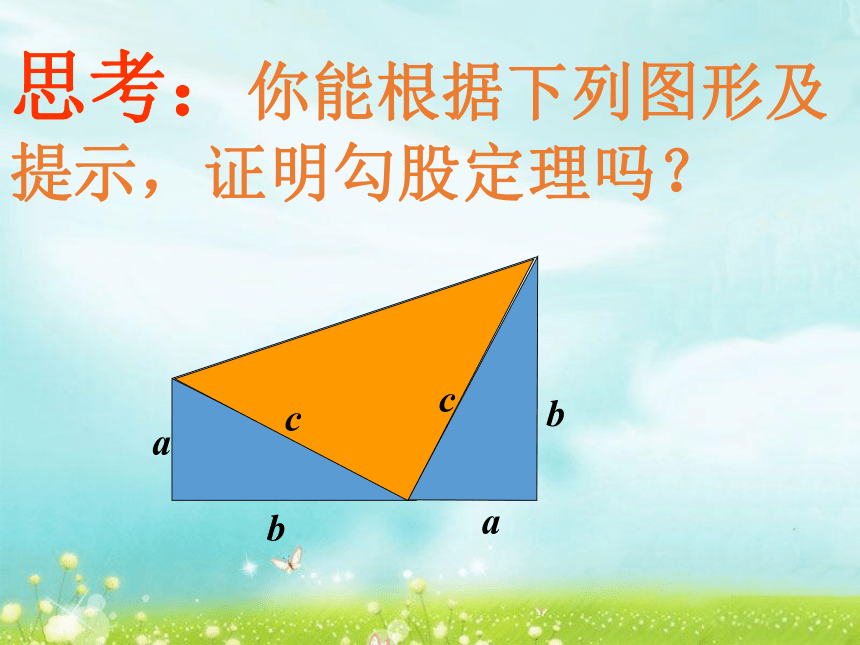
图形面积的两个基本性质很重要,根据这两个性质,我们可以借助于适当的辅助线割补多边形,割补后所成新图形的面积和原图形面积相等,这种方法叫做面积割补法.a2b2bacc2a2c2b2a2+b2=c2勾股定理的应用 在直角三角形中,如果已知任意两条边长,就可以求出第三条边长. Rt△ABC中,∠C=90o,∠A、∠B、∠C所对的边分别是a、b、c,则有a2+b2=c2故AD的长为12cm.在Rt△ADB中,由勾股定理得
AD2+BD2 =AB2 ,练习: 若三角形三内角的度数之比为1:2:3,则它的三条边的比为多少?思考:你能根据下列图形及提示,证明勾股定理吗?abccab邮递员从车站O正东1km的邮局A出发,先向正北走了3km到B,又向正西走了4km到C,最后再向正南走了6km到D,那么最终该邮递员与邮局的距离为多少km? ABCDO分析 根据题意,先画出水池截面示意图, 如图1-18.
设AB 为芦苇,BC 为芦苇出水部分,即1 尺,将芦苇拉向岸边,其顶部B点恰好碰到岸边B′.在Rt△ACB′中, 根据勾股定理,得
x2 + 52 =(x+ 1)2,答:水池的深度为12尺,芦苇长为13尺.图1-18因为正方形池塘边长为10尺, 所以
B′C = 5尺.解得 x=12.
则芦苇长为13尺.在一个内腔长30cm、宽40 cm、高50 cm的木箱中放一根笔直的细玻璃管,这根玻璃管的长度至多为多少cm? ACBD练习在图中,如果在箱内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要爬多远? CD图①305040CDA.B.CCDA.B.图②直角三角形有哪些性质? (1)有一个角是直角; (2)两个锐角的和为90°(互余 ); (3)两直角边的平方和等于斜边的平方 . 反之,一个三角形满足什么条件
才能是直角三角形呢?忆一忆(1)有一个角是直角的三角形是直角三角形; (2)有两个角的和为90°的三角形是直角三角形; (3)如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2
,那么这个三角形是直角三角形吗一个三角形满足什么条件才能是直角三角形????你想知道这是什么道理吗?据说,古埃及人曾用下面的方法画直角:
他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处. 请比较上述每个三角形的两条较短边的平方和与最长边的平方之间的大小关系. 锐角三角形钝角三角形直角三角形勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 .a2 + b2 = c2反过来分析 根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最长边的平方.(2) ∵ 122 + 152 = 369, 202 = 400,
∴ 122 + 152≠202.
∴ 这个三角形不是直角三角形.(1)a = 6,b = 8,c = 10;(2)a = 12,b = 15,c = 20.例4如图1-21,在△ABC 中,已知AB = 10,BD = 6, AD = 8,AC = 17. 求DC的长.图1-21 练习1、下面以a,b,c为边长的△ABC是不是直角三角形?如果是那么哪一个角是直角?(1) a=6 b=8 c=10 ____ _____ ;(2) a=12 b=8 c=15 ____ _____ ;(3) a=8 b=6 c=5 _____ _____ ;是 不是不是 是∠ C=90°∠ B=90°练习2、满足下列条件△ABC, 不是直角三角形的是 ( )
A、b2 = a2 - c2
B、a:b:c=3:4:5
C、∠C=∠B - ∠A
D、∠A:∠B :∠C =3:4:5D解:如图,设每两个结的 距离为a(a>0),则AC=3a,BC=4a,AB=5a. 据说,古埃及人曾用下面的方法画直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.再 见!
3 4 5
6 8 10
5 12 13
……勾2+股2=弦2勾股勾股定理
直角三角形两直角边a、b的平方和,等于斜边c的平方. 即a2+b2=c2面积证法(面积割补法) 图形面积的有关性质:
(1)两个图形全等,它们的面积相等;
(2)一个图形的面积,等于它的各部分面积的和.
图形面积的两个基本性质很重要,根据这两个性质,我们可以借助于适当的辅助线割补多边形,割补后所成新图形的面积和原图形面积相等,这种方法叫做面积割补法.a2b2bacc2a2c2b2a2+b2=c2勾股定理的应用 在直角三角形中,如果已知任意两条边长,就可以求出第三条边长. Rt△ABC中,∠C=90o,∠A、∠B、∠C所对的边分别是a、b、c,则有a2+b2=c2故AD的长为12cm.在Rt△ADB中,由勾股定理得
AD2+BD2 =AB2 ,练习: 若三角形三内角的度数之比为1:2:3,则它的三条边的比为多少?思考:你能根据下列图形及提示,证明勾股定理吗?abccab邮递员从车站O正东1km的邮局A出发,先向正北走了3km到B,又向正西走了4km到C,最后再向正南走了6km到D,那么最终该邮递员与邮局的距离为多少km? ABCDO分析 根据题意,先画出水池截面示意图, 如图1-18.
设AB 为芦苇,BC 为芦苇出水部分,即1 尺,将芦苇拉向岸边,其顶部B点恰好碰到岸边B′.在Rt△ACB′中, 根据勾股定理,得
x2 + 52 =(x+ 1)2,答:水池的深度为12尺,芦苇长为13尺.图1-18因为正方形池塘边长为10尺, 所以
B′C = 5尺.解得 x=12.
则芦苇长为13尺.在一个内腔长30cm、宽40 cm、高50 cm的木箱中放一根笔直的细玻璃管,这根玻璃管的长度至多为多少cm? ACBD练习在图中,如果在箱内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要爬多远? CD图①305040CDA.B.CCDA.B.图②直角三角形有哪些性质? (1)有一个角是直角; (2)两个锐角的和为90°(互余 ); (3)两直角边的平方和等于斜边的平方 . 反之,一个三角形满足什么条件
才能是直角三角形呢?忆一忆(1)有一个角是直角的三角形是直角三角形; (2)有两个角的和为90°的三角形是直角三角形; (3)如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2
,那么这个三角形是直角三角形吗一个三角形满足什么条件才能是直角三角形????你想知道这是什么道理吗?据说,古埃及人曾用下面的方法画直角:
他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处. 请比较上述每个三角形的两条较短边的平方和与最长边的平方之间的大小关系. 锐角三角形钝角三角形直角三角形勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 .a2 + b2 = c2反过来分析 根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最长边的平方.(2) ∵ 122 + 152 = 369, 202 = 400,
∴ 122 + 152≠202.
∴ 这个三角形不是直角三角形.(1)a = 6,b = 8,c = 10;(2)a = 12,b = 15,c = 20.例4如图1-21,在△ABC 中,已知AB = 10,BD = 6, AD = 8,AC = 17. 求DC的长.图1-21 练习1、下面以a,b,c为边长的△ABC是不是直角三角形?如果是那么哪一个角是直角?(1) a=6 b=8 c=10 ____ _____ ;(2) a=12 b=8 c=15 ____ _____ ;(3) a=8 b=6 c=5 _____ _____ ;是 不是不是 是∠ C=90°∠ B=90°练习2、满足下列条件△ABC, 不是直角三角形的是 ( )
A、b2 = a2 - c2
B、a:b:c=3:4:5
C、∠C=∠B - ∠A
D、∠A:∠B :∠C =3:4:5D解:如图,设每两个结的 距离为a(a>0),则AC=3a,BC=4a,AB=5a. 据说,古埃及人曾用下面的方法画直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.再 见!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
