1.3 直角三角形全等的判定 课件1

课件15张PPT。1.3 直角三角形全等的判定复习回顾问题1. 判定两个三角形全等有哪些方法？问题2. 对于两个直角三角形，除了可以运用一般
三角形全等的判定方法外，是否还有其他的判定
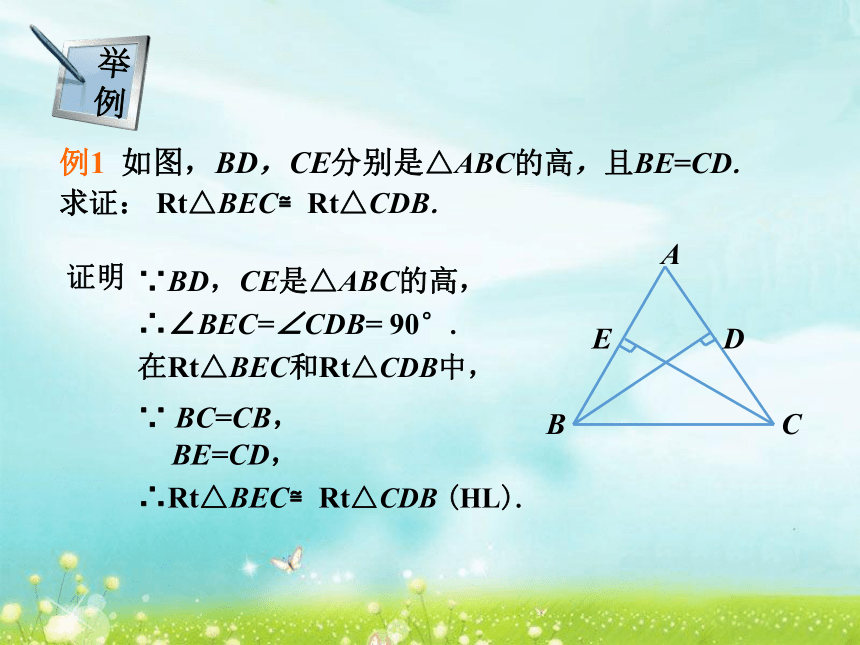
方法呢？(SSS)、(SAS)、(ASA)、(AAS)如图，在Rt△ABC和Rt△A′B′C′中，已知 AB=A′B′， AC= A′C′， ∠ACB=∠ A′C′B′= 90°， 那么Rt△ABC和Rt△A′B′C′全等吗？在Rt△ABC和Rt△A′B′C′中，∵AB=A′B′， AC= A′C′， 根据勾股定理， BC2= AB2-AC2， B′C′2= A′B′2 - A′C′2 ∴ BC = B′C′.∴Rt△ABC≌Rt△A′B′C′.斜边、直角边定理 斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).直角三角形全等的判定定理例1 如图，BD，CE分别是△ABC的高，且BE=CD.
求证： Rt△BEC≌Rt△CDB.证明∵BD，CE是△ABC的高，∴∠BEC=∠CDB= 90°.在Rt△BEC和Rt△CDB中，∵ BC=CB，∴Rt△BEC≌Rt△CDB (HL).BE=CD，例2 已知一直角边和斜边，求作直角三角形.已知：如图，线段a，c (c>a).作法求作： Rt△ABC，使AB=c， BC=a .(1)作∠MCN= 90°.(2)在CN上截取CB，使CB=a.(3)以点B为圆心，以c为半径
画弧，交CM于点A，连接AB.则△ABC为所求作的直角三角形.cBA●●练习1两个锐角对应相等的两个直角三角形全等吗？
两条直角边对应相等的两个直角三角形全等吗？
有任意的两条边对应相等的两个直角三角形全等吗？
判定两个直角三角形全等，共有多少种方法？
答：不一定全等.答：全等.答：全等.答：共有SAS，ASA，AAS，SSS，HL 5种方法.练习2已知：如图，AC＝BD，AD⊥AC，BC⊥BD．
求证：AD＝BC.
证明：连接DC.
∵ AD⊥AC，BC⊥BD，
∴∠A=∠B= 90°.
在Rt△ADC和Rt△BCD中，
DC=CD，
AC=BD，
∴Rt△ADC≌Rt△BCD (HL).
∴AD=BC.
1.已知：如图，在△ABC和△ABD中，AC⊥BC， AD⊥BD，垂足分别为C，D，AD=BC，求证： △ABC≌△BAD.课外练习2.已知：如图，在△ABC和△DEF中，AP、DQ分别是高， 且AB=DE，AP=DQ，∠BAC=∠EDF，
求证：△ABC≌△DEF已知：如图，点A、B、C、D在同一条直线上， EA⊥AD，FD⊥AD，AE=DF，AB=DC .
求证：∠ACE=∠DBF. ∵ AB=DC，
∴ AB+BC=DC+BC， 即 AC=BD.
又∵ AE=DF，
∠EAC=∠FDB =90°.
∴ △AEC≌△DFB
∴ ∠ACE=∠DBF.证明今天所学的直角三角形全等的判定定理是什么？
直角三角形全等有几种判定方法？再 见！