4.3 一次函数的图象 课件

课件37张PPT。4.3 一次函数的图象复习旧知一次函数的定义： 若两个变量x，y间的关系式可以表示成
(k、b为常数，k≠0)的形式，则称
y是x是一次函数，其中x为自变量，y为因变量. 一般地，形如 y=kx(k是常数，k≠0)的函数，叫做正比例函数，其中k叫做比例系数.1、在下列函数2、函数有哪些表示方法？图象法、列表法、关系式法是一次函数的是 ，
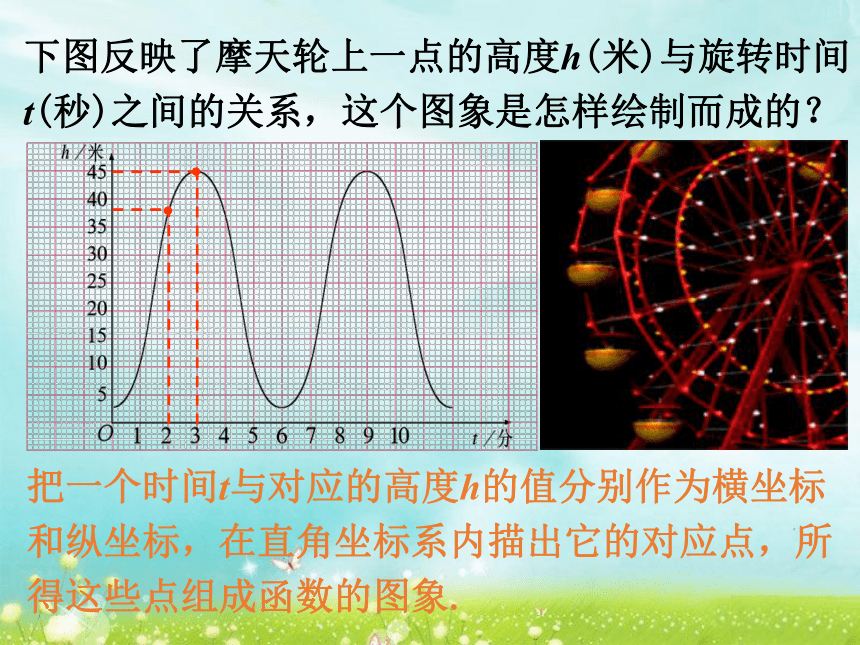
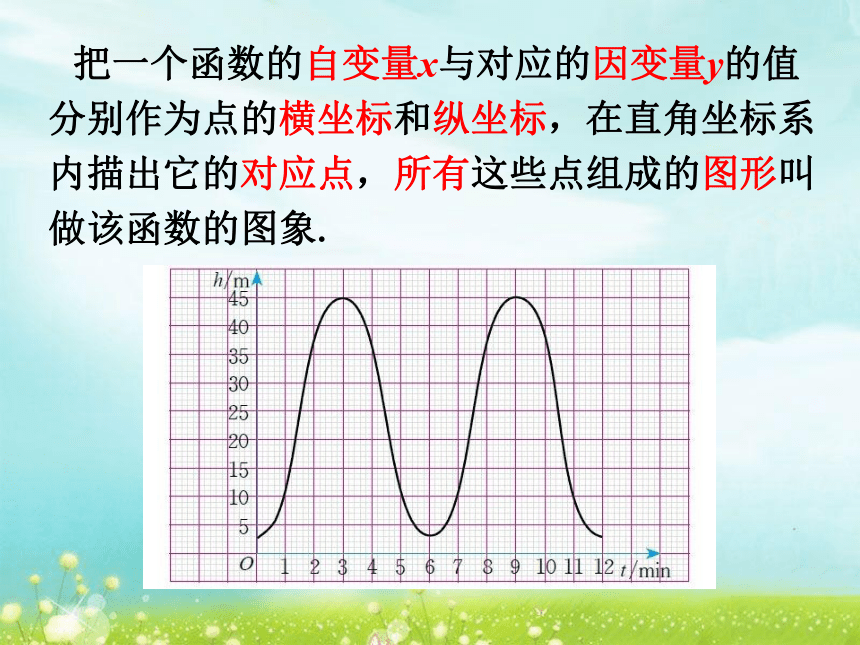
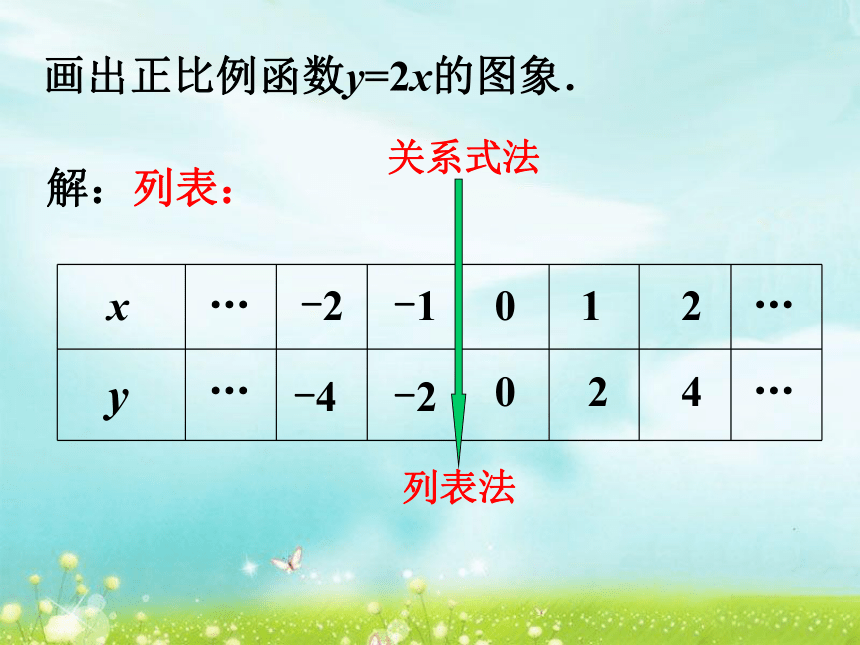
是正比例函数的是 .(2)，(4)(2)三种方法可以相互转化它们之间有什么关系？3、你能将关系式法转化成图象法吗？什么是函数的图象？下图反映了摩天轮上一点的高度h(米)与旋转时间t(秒)之间的关系，这个图象是怎样绘制而成的？把一个时间t与对应的高度h的值分别作为横坐标和纵坐标，在直角坐标系内描出它的对应点，所得这些点组成函数的图象. 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标，在直角坐标系内描出它的对应点，所有这些点组成的图形叫做该函数的图象.画出正比例函数y=2x的图象．解：列表：
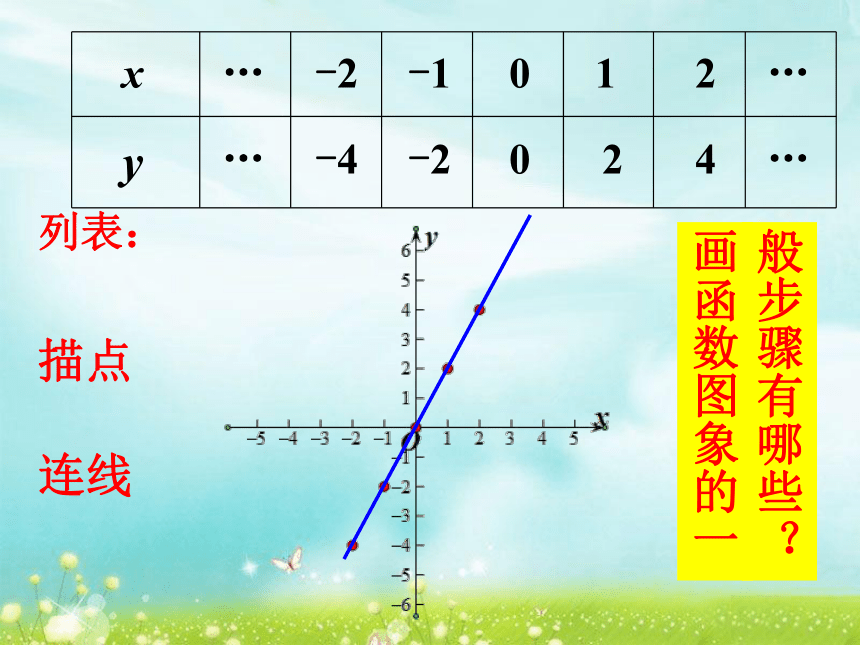
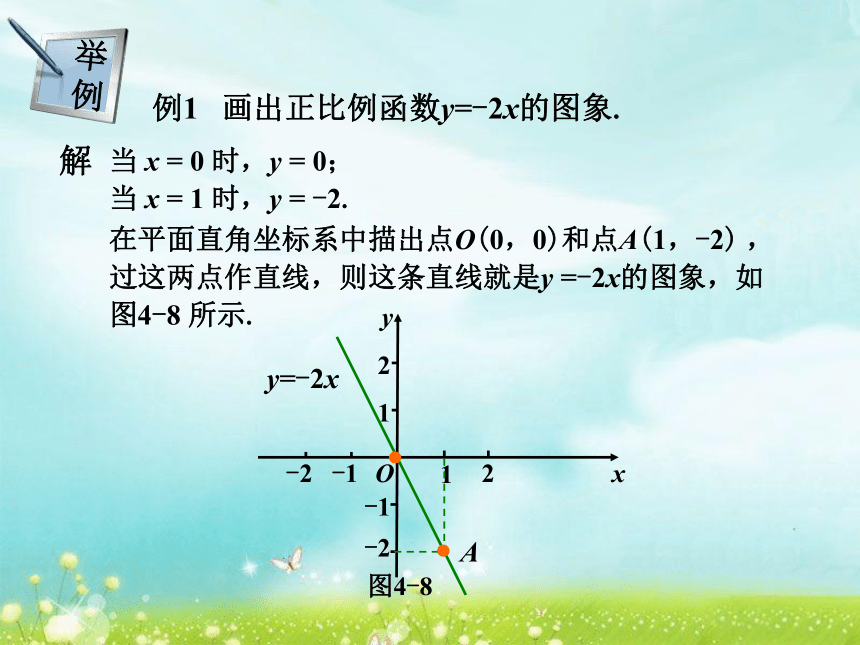
xy100-12-2…………24-2-4关系式法列表法描点连线画函数图象的一般步骤有哪些？列表：例1 画出正比例函数y=-2x的图象.在平面直角坐标系中描出点O(0，0)和点A(1，-2) ，
过这两点作直线，则这条直线就是y =-2x的图象，如
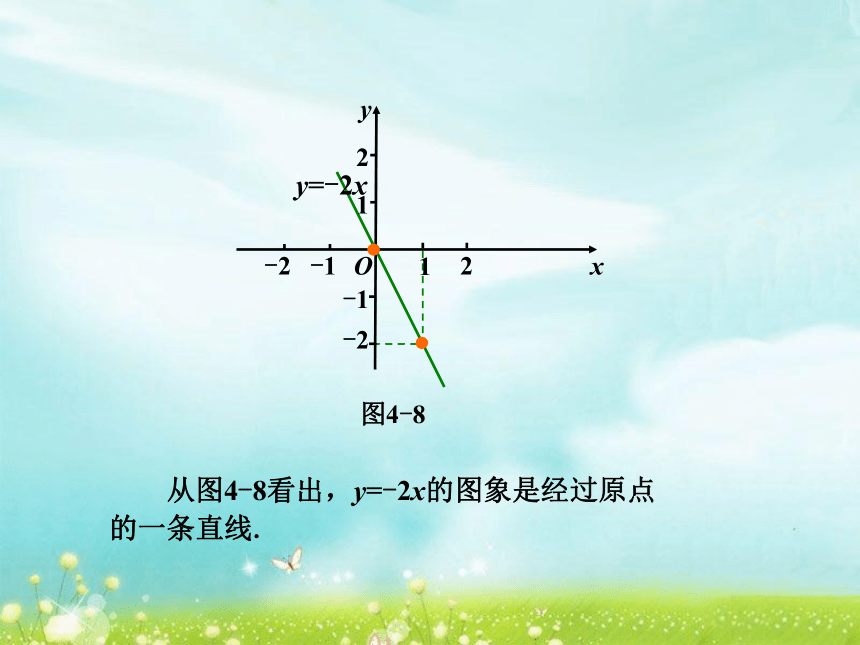
图4-8 所示.图4-8y=-2xA 从图4-8看出，y=-2x的图象是经过原点的一条直线.图4-8y=-2x(1)满足关系式y=-2x的x，y所对应的点
(x，y)都在正比例函数y=-2x的图象上吗？(2) 正比例函数y=-2x的图象上的
点(x，y)都满足关系式y=-2x吗？相同点：
不同点：函数y=2x的图象经过第 象限，从左向右 ，函数y=－2x的图象经过第 象限.从左向右 .呈上升状态一、三呈下降状态二、四两图象都是经过原点的一条直线正比例函数y=kx的图象是一条经过原点的直线.因此，画正比例函数图象时，只要再确定一个点，过这点与原点画直线就可以了.(3)正比例函数y=kx的图象有何特点？你是怎样理解的？ 正比例函数图象经过点(0，0)和点(1，k)(2)画出这个函数的图象； 在平面直角坐标系中， 先画出函数y = 2x 的
图象，然后探索y = 2x+3 的图象是什么样的图形，
猜测y = 2x+3的图象与y = 2x的图象有什么关系？ 先取自变量x的一些值，算出y = 2x，y = 2x+3
对应的函数值，列成表格如下：y = 2x+3… -3 -2 -1 0 1 2 3 …… -6 -4 -2 0 2 4 6 …
… -3 -1 1 3 5 7 9 … 从上表可以看出，横坐标相同，y = 2x+3的
点的纵坐标比y = 2x的点的纵坐标大3，于是将
y = 2x的图象向上平移3 个单位，就得到y = 2x+3
的图象，如图4-11. 由于平移把直线变成与它平行的直线，因此
y = 2x+3的图象是与y = 2x平行的一条直线. 类似地，可以证明，一次函数y = kx+b的图
象是一条直线，它与正比例函数y = kx 的图象平
行，一次函数y = kx+b (k，b为常数，k≠0)的
图象可以看作由直线y = kx平移│b│个单位长度
而得到(当b＞0时，向上平移； 当b＜0时，向下平移). 由于两点确定一条直线，因此画一次函数的
图象，只要描出图象上的两个点，然后过这两点
作一条直线即可. 我们常常把这条直线叫作“直线
y = kx+b”.例3 画出一次函数y = -2x-3的图象.在平面直角坐标系中描出两点A(0，-3)，
B(1，-5)，过这两点作直线，则这条直线是
一次函数y = -2x-3的图象，如图4-12.探 索 活 动 观察这两个函数的图像，你有什么发现？探 索 活 动 如何理解图像的上升、下降？　　一次函数图像的上升、下降与什么量有关？探 索 活 动 B 点在 A 点右上方．　　函数值 y 随 x值的增大而增大．增大 函数图像上升．探 索 活 动 怎样理解函数图像的下降？函数值 y 随 x 值的增大而减小．函数图像下降．　　观察C、D 两点的位置及坐标，你有什么发现？D 点在 C 点右下方．增大减小探 索 发 现 　　观察以上两组图像，函数图像的上升、下降与什么量有关？y ＝－2x＋4探 索 发 现 y ＝　x－3y =－2x＋4(1)当k＞0时，y随x的增大而增大，从左到右看函数的图像是上升的； (2)当k＜0时，y随x的增大而减小，从左到右看函数的图像是下降的． 在一次函数y＝kx＋b中：总 结 概 括 y =　x－3例4 图4-13 描述了某一天小亮从家骑车去书店购书，
然后又骑车回家的情况. 你能说出小亮在路上的
情形吗？图4-13 第三段是与x 轴有交点的线段BC. 从横坐标看出，
小亮路上花了40min.当横坐标从60 变化到100 时，
纵坐标均匀减少，这说明小亮从书店出发匀速前进
40min，返回家中. 第二段是与x 轴平行的一条线段AB，当横坐标从30 变化到60时，纵坐标没有变化，这说明小亮在书店购书待了30min. 实际上，我们还可以比较第一段与第三段线段，
发现第一段更“陡”，这说明去书店的速度更快，
而回家的速度要慢一些. 练 习 应 用 1. 一次函数y＝k x＋b的图像如图所示.（1）求函数关系式．（2）观察图像
当x为何值时，y ＞ 0 ？
当x为何值时，y ＜ 0 ？ 2．一次函数y＝2x－3的图像经过（ ）A．第一、二、三象限．B．第一、二、四象限．C．第一、三、四象限．D．第二、三、四象限． 练 习 应 用 3．已知一次函数y ＝(2k－1)x＋3k＋2．（1）当k＝_____时，直线经过原点.（4）当k__时，与 y 轴的交点在 x 轴的下方.（3）当k______时，y 随 x 的增大而增大.（5）当k_____时，它的图像经过二、三、四象限.（2）当k___时，直线与 x 轴交于点(－1，0). 练 习 应 用 应 用 提 高 　　4．一次函数y＝kx＋b中，kb＞0，且y随x的增大而减小，则它的图像大致为（ ）DCBA应 用 提 高 5．直线y＝kx＋b与直线y＝kbx，它们在同一个坐标系中的图像大致为（ ）