1.2 直角三角形的性质和判定(Ⅱ) 教案
文档属性
| 名称 | 1.2 直角三角形的性质和判定(Ⅱ) 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-28 12:36:19 | ||
图片预览

文档简介
1.2
直角三角形的性质和判定(Ⅱ)
教案
教学目标
1.知识与技能:使学生掌握勾股定理,培养在实际生活中发现问题总结规律的意识和能力.
2.过程与方法:了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理.
3.情感、态度与价值观:介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习.
教学重点、难点
1.重点:勾股定理的内容及证明.
2.难点:勾股定理的证明.
3.难点的突破方法:几何学的产生,源于人们对土地面积的测量需要.在古埃及,尼罗河每年要泛滥一次;洪水给两岸的田地带来了肥沃的淤积泥土,但也抹掉了田地之间的界限标志.水退了,人们要重新画出田地的界线,就必须再次丈量、计算田地的面积.几何学从一开始就与面积结下了不解之缘,面积很早就成为人们认识几何图形性质与争鸣几何定理的工具.本节课采用拼图的方法,使学生利用面积相等对勾股定理进行证明.其中的依据是图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变.
教学过程
(一)、新课引入
已知树高6米,在树梢上有一猫头鹰,猫头鹰从树梢斜飞落地抓老鼠,落点与树根相距8米,那么猫头鹰至少飞过多少米?
(二)、探究定理
1、画一画:
让学生动手画一个直角边长为3cm和4cm的直角△ABC,用刻度尺量出AB的长.
以上这个事实是我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五.”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5.
2、做一做
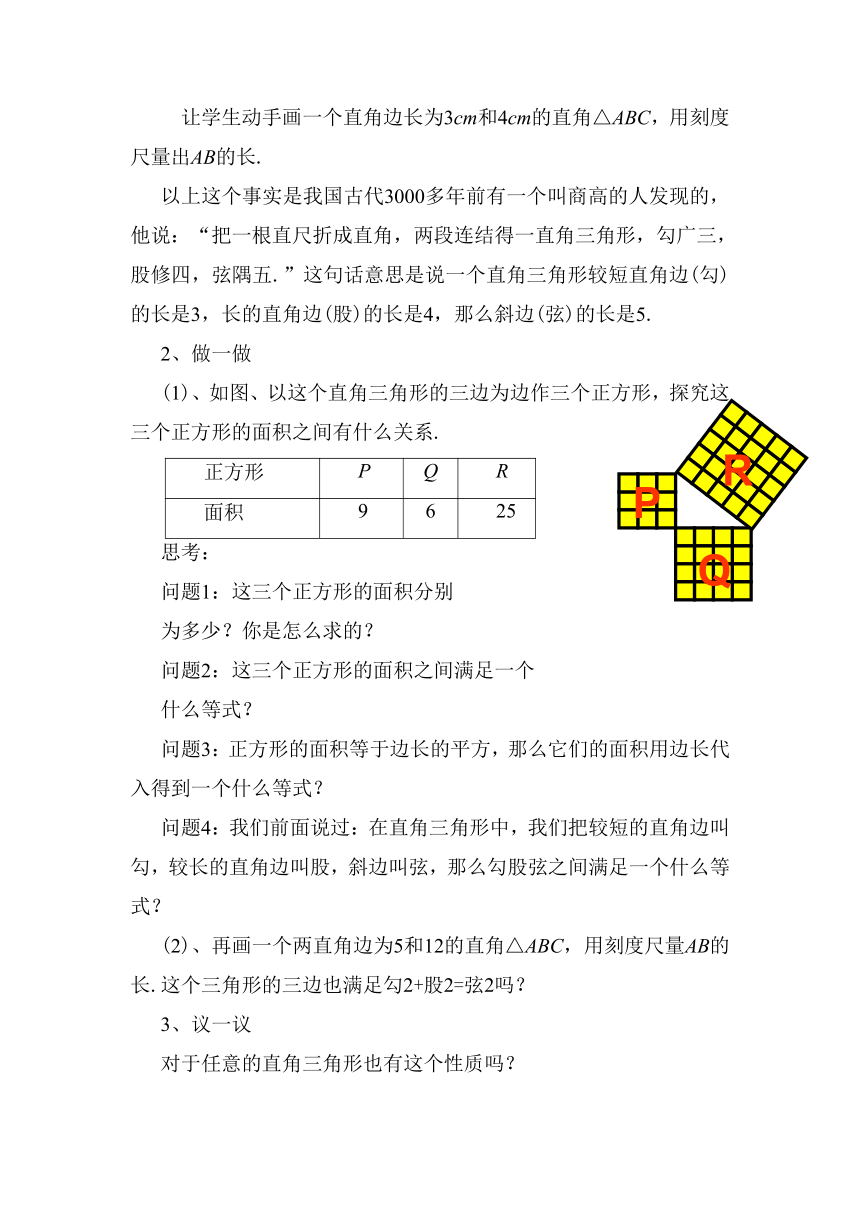
(1)、如图、以这个直角三角形的三边为边作三个正方形,探究这三个正方形的面积之间有什么关系.
正方形
P
Q
R
面积
9
6
25
思考:
问题1:这三个正方形的面积分别
为多少?你是怎么求的?
问题2:这三个正方形的面积之间满足一个
什么等式?
问题3:正方形的面积等于边长的平方,那么它们的面积用边长代入得到一个什么等式?
问题4:我们前面说过:在直角三角形中,我们把较短的直角边叫勾,较长的直角边叫股,斜边叫弦,那么勾股弦之间满足一个什么等式?
(2)、再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长.这个三角形的三边也满足勾2+股2=弦2吗?
3、议一议
对于任意的直角三角形也有这个性质吗?
4、猜一猜
直角三角形的两直角边的平方和等于斜边的平方.即在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c,有
a2+b2=c2
【过渡语】
猜想的结论是否正确须经过严格论证.证明该结论很难,许多数学家经过艰辛的努力,已想出很多种巧妙的证法,下面让大家体验一下其中的一种证法:我国三国时期的数学家赵爽创造的一种证法.
5、探一探(小组活动)
⑴、请同学们拿出准备好的4个全等的直角三角形模型,最好是有颜色的吹塑纸,三边分别标好a,b,c,拼出一个边长为c的正方形,利用面积相等进行证明(赵爽弦图,如图).
【小组合作探究】,思考:
问题1:你拼的四边形是正方形吗?为什么?
问题2:图中分别有几个正方形?几个直角三角形?
问题3:大正方形由哪几个图形构成?
问题4:它们的面积之间满足什么样的关系?
问题5:分别怎么来表示它们的面积?
⑵、证明:如图2左(赵爽弦图)所示,其等量关系为:
4S△+S小正=S大正即
4×ab+(b-a)2=c2,
6、归纳总结
勾股定理:直角三角形两直角边的平方和等于斜边的平方.即在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c,有
a2+b2=c2.
我国称这个结论为“勾股定理”,西方称它为“毕达哥拉斯定理”,为什么呢?
(1)介绍《周髀算经》中西周的商高(公元一千多年前)发现了勾三股四弦五这个规律
(2)介绍西方毕达哥拉斯于公元前582~493时期发现了勾股定理;
(3)对比以上事实对学生进行爱国主义教育,激励他们奋发向上.
说明:直角三角形的边长为正数,所以取算术平方根.
问题1:勾股定理对所有的三角形都适用吗?为什么?
问题2:勾股定理的条件是什么?结论是什么?
结论:勾股定理揭示了在直角三角形中已知任意二边可以求第三边.
(三)、勾股定理的应用
1、例题分析:
例1.如课本第11页图1-15,在等腰三角形ABC中,已知AB=AC=13cm,BC=10cm,AD⊥BC于点D,你能算出BC边上的高AD的长吗?
方法小结:利用勾股定理建立方程.
例2.(“引葭赴岸”问题)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”意思是:有一个边长为10
尺的正方形池塘,一棵芦苇生长在池的中央,其出水部分为1尺.如果将芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好碰到池边的水面.问水深与芦苇长各为多少?
(四)解决问题:
已知树高6米,在树梢上有一猫头鹰,猫头鹰从树梢斜飞落地抓老鼠,落点与树根相距8米,那么猫头鹰至少飞过多少米?
(五)小结:
1、本节课我们经历了怎样的过程?
2、本节课我们学到了什么?
3、学了本节课后我们有什么感想?
Q
P
R
b
b
b
b
c
c
c
c
a
a
a
a
直角三角形的性质和判定(Ⅱ)
教案
教学目标
1.知识与技能:使学生掌握勾股定理,培养在实际生活中发现问题总结规律的意识和能力.
2.过程与方法:了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理.
3.情感、态度与价值观:介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习.
教学重点、难点
1.重点:勾股定理的内容及证明.
2.难点:勾股定理的证明.
3.难点的突破方法:几何学的产生,源于人们对土地面积的测量需要.在古埃及,尼罗河每年要泛滥一次;洪水给两岸的田地带来了肥沃的淤积泥土,但也抹掉了田地之间的界限标志.水退了,人们要重新画出田地的界线,就必须再次丈量、计算田地的面积.几何学从一开始就与面积结下了不解之缘,面积很早就成为人们认识几何图形性质与争鸣几何定理的工具.本节课采用拼图的方法,使学生利用面积相等对勾股定理进行证明.其中的依据是图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变.
教学过程
(一)、新课引入
已知树高6米,在树梢上有一猫头鹰,猫头鹰从树梢斜飞落地抓老鼠,落点与树根相距8米,那么猫头鹰至少飞过多少米?
(二)、探究定理
1、画一画:
让学生动手画一个直角边长为3cm和4cm的直角△ABC,用刻度尺量出AB的长.
以上这个事实是我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五.”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5.
2、做一做
(1)、如图、以这个直角三角形的三边为边作三个正方形,探究这三个正方形的面积之间有什么关系.
正方形
P
Q
R
面积
9
6
25
思考:
问题1:这三个正方形的面积分别
为多少?你是怎么求的?
问题2:这三个正方形的面积之间满足一个
什么等式?
问题3:正方形的面积等于边长的平方,那么它们的面积用边长代入得到一个什么等式?
问题4:我们前面说过:在直角三角形中,我们把较短的直角边叫勾,较长的直角边叫股,斜边叫弦,那么勾股弦之间满足一个什么等式?
(2)、再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长.这个三角形的三边也满足勾2+股2=弦2吗?
3、议一议
对于任意的直角三角形也有这个性质吗?
4、猜一猜
直角三角形的两直角边的平方和等于斜边的平方.即在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c,有
a2+b2=c2
【过渡语】
猜想的结论是否正确须经过严格论证.证明该结论很难,许多数学家经过艰辛的努力,已想出很多种巧妙的证法,下面让大家体验一下其中的一种证法:我国三国时期的数学家赵爽创造的一种证法.
5、探一探(小组活动)
⑴、请同学们拿出准备好的4个全等的直角三角形模型,最好是有颜色的吹塑纸,三边分别标好a,b,c,拼出一个边长为c的正方形,利用面积相等进行证明(赵爽弦图,如图).
【小组合作探究】,思考:
问题1:你拼的四边形是正方形吗?为什么?
问题2:图中分别有几个正方形?几个直角三角形?
问题3:大正方形由哪几个图形构成?
问题4:它们的面积之间满足什么样的关系?
问题5:分别怎么来表示它们的面积?
⑵、证明:如图2左(赵爽弦图)所示,其等量关系为:
4S△+S小正=S大正即
4×ab+(b-a)2=c2,
6、归纳总结
勾股定理:直角三角形两直角边的平方和等于斜边的平方.即在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c,有
a2+b2=c2.
我国称这个结论为“勾股定理”,西方称它为“毕达哥拉斯定理”,为什么呢?
(1)介绍《周髀算经》中西周的商高(公元一千多年前)发现了勾三股四弦五这个规律
(2)介绍西方毕达哥拉斯于公元前582~493时期发现了勾股定理;
(3)对比以上事实对学生进行爱国主义教育,激励他们奋发向上.
说明:直角三角形的边长为正数,所以取算术平方根.
问题1:勾股定理对所有的三角形都适用吗?为什么?
问题2:勾股定理的条件是什么?结论是什么?
结论:勾股定理揭示了在直角三角形中已知任意二边可以求第三边.
(三)、勾股定理的应用
1、例题分析:
例1.如课本第11页图1-15,在等腰三角形ABC中,已知AB=AC=13cm,BC=10cm,AD⊥BC于点D,你能算出BC边上的高AD的长吗?
方法小结:利用勾股定理建立方程.
例2.(“引葭赴岸”问题)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”意思是:有一个边长为10
尺的正方形池塘,一棵芦苇生长在池的中央,其出水部分为1尺.如果将芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好碰到池边的水面.问水深与芦苇长各为多少?
(四)解决问题:
已知树高6米,在树梢上有一猫头鹰,猫头鹰从树梢斜飞落地抓老鼠,落点与树根相距8米,那么猫头鹰至少飞过多少米?
(五)小结:
1、本节课我们经历了怎样的过程?
2、本节课我们学到了什么?
3、学了本节课后我们有什么感想?
Q
P
R
b
b
b
b
c
c
c
c
a
a
a
a
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
