24.1.2垂径定理 课件
图片预览



文档简介
课件28张PPT。人教版九年级上册24.1.2垂径定理 问题:你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 创设情境:1.过圆上一固定点可以作圆的最长弦有( )条.
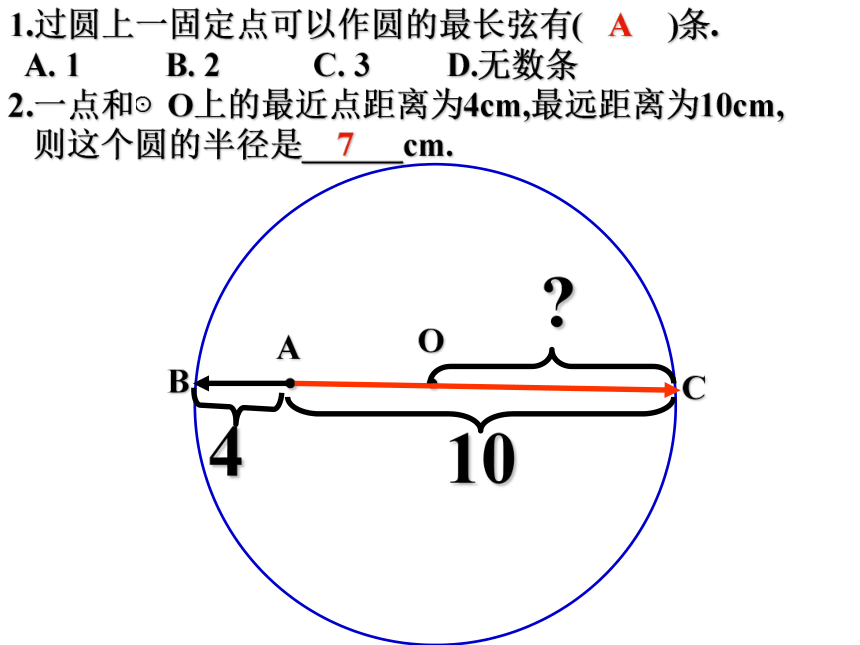
A. 1 B. 2 C. 3 D.无数条
2.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
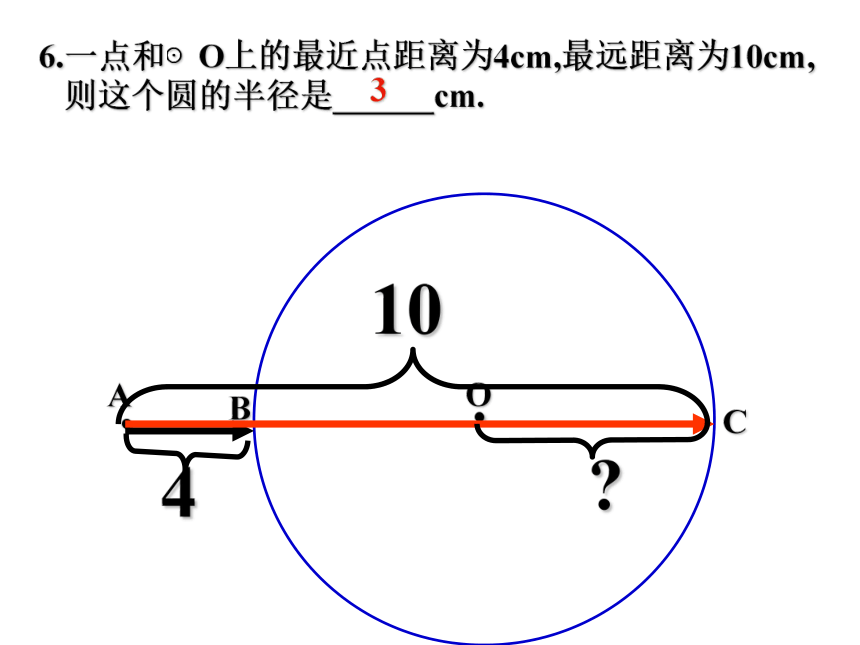
则这个圆的半径是______cm.A7.OAC.B410?6.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是______cm.37.OAC.B104? 由此你能得到圆的什么特性? 可以发现:圆是轴对称图形。任何一条直径所在直线都是它的对称轴. 不借助任何工具,你能找到圆形纸片的圆心吗?活动一1、在已有的圆上标出圆心,沿一条直径对折。
2、在对折后的半圆弧上,用笔在同一位置上的正反面做一个标记
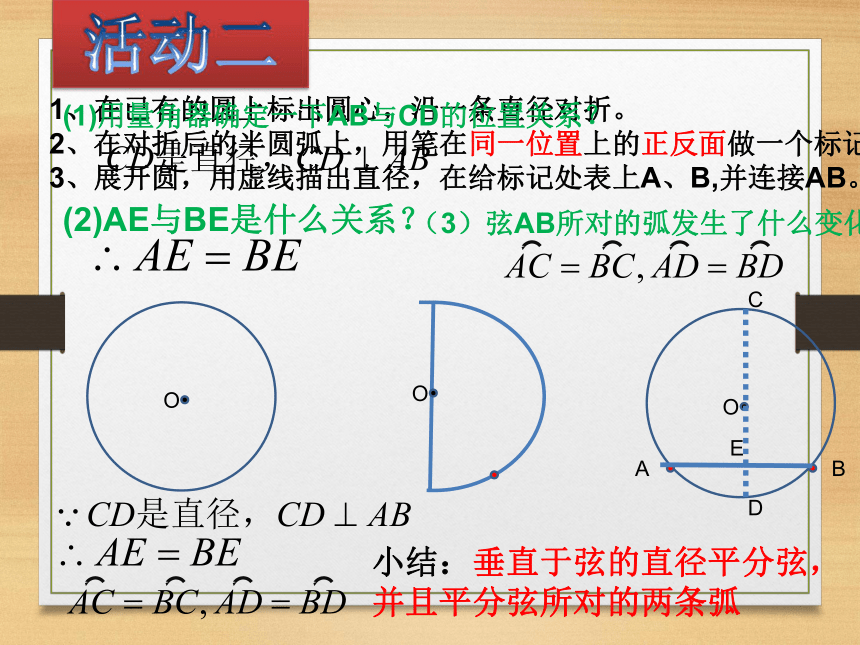
3、展开圆,用虚线描出直径,在给标记处表上A、B,并连接AB。ABCDE(1)用量角器确定一下AB与CD的位置关系?(2)AE与BE是什么关系?(3)弦AB所对的弧发生了什么变化?小结:垂直于弦的直径平分弦,
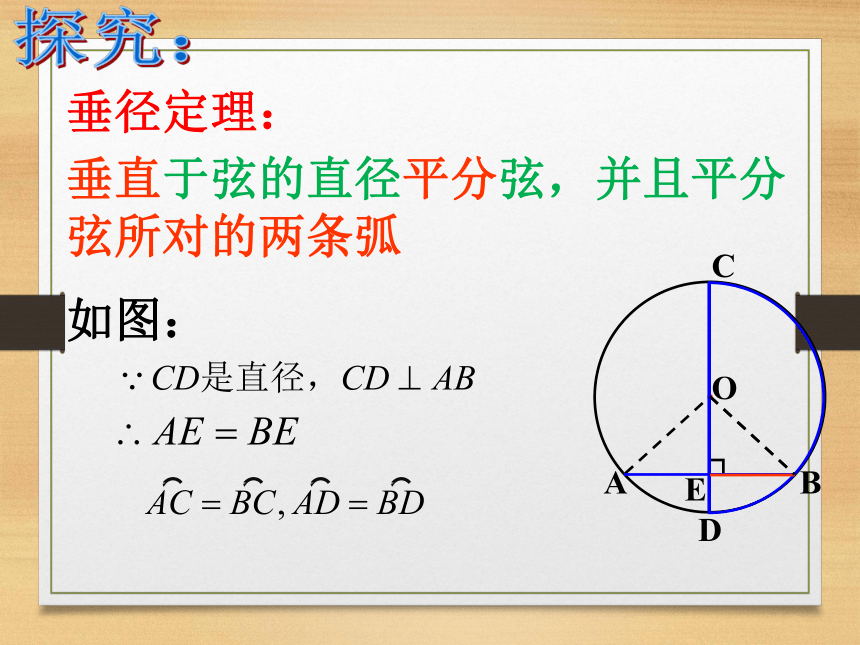
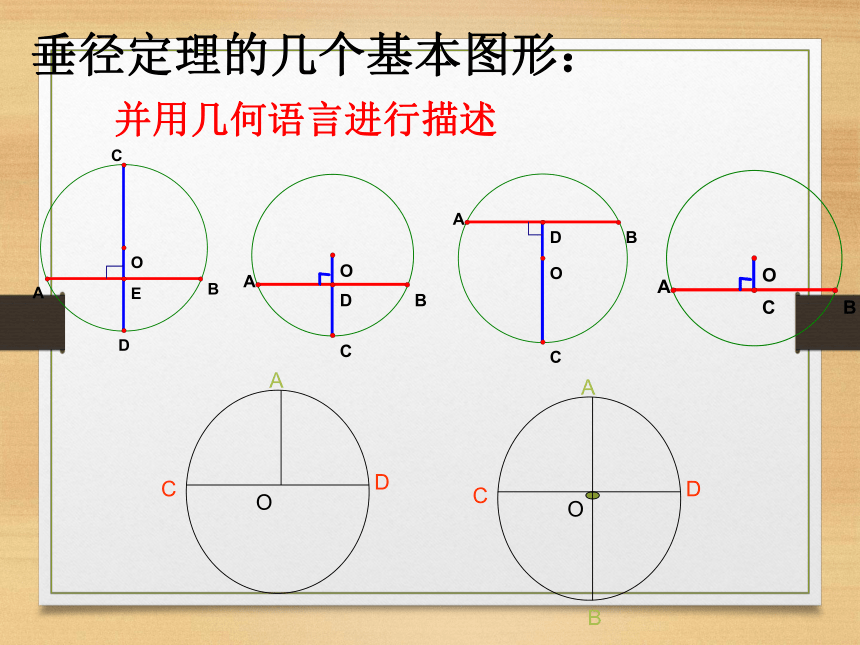
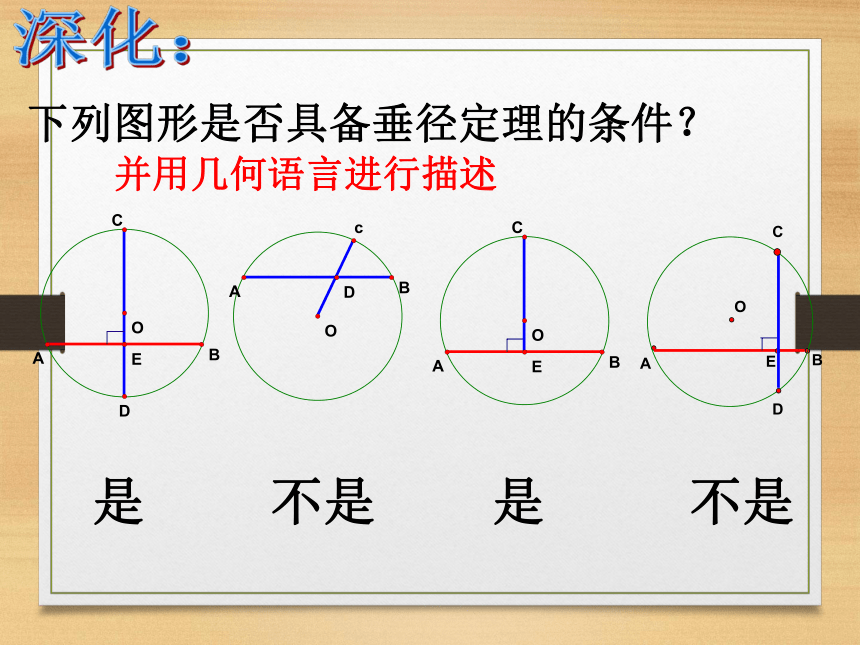
并且平分弦所对的两条弧探究:·OABCDE垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧如图:垂径定理的几个基本图形:BCDAO并用几何语言进行描述下列图形是否具备垂径定理的条件?是不是是不是深化:并用几何语言进行描述ABCDE垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧如图:课堂小结例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径.1巩固:11、如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是( )D、∠COE=∠DOEB、CE=DEC、OE=AE2、如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB= cm。·OABE解:连接OA,∵ OE⊥AB∴ AB=2AE=16cm3、如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。·OABE解:过点O作OE⊥AB于E,连接OA即⊙O的半径为5cm.2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证:四边形ADOE是正方形.·OABCDE证明:∴四边形ADOE为矩形,又 ∵AC=AB,∴ AE=AD.∴ 四边形ADOE为正方形.6.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是 。8cm4.半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是 。5. ⊙O的直径为10cm,圆心O到弦AB的 距离为3cm,则弦AB的长是 。二、填空: 如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE在来!你行吗?解:答:⊙O的半径为5cm.在Rt △ AOE 中 14、如图,CD是⊙O的直径,弦AB⊥CD于E,CE=1,AB=10,求直径CD的长。 2:已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE实际上,往往只需从圆心作一条与弦垂直的线段.就可以利用垂径定理来解决有关问题了. 已知:⊙O中弦AB∥CD。
求证:AC=BD⌒⌒.夹在两条平行弦间的弧相等.M●OABCD1.两条弦在圆心的同侧●OABCD2.两条弦在圆心的两侧1、⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___ .EFEF10861068210861086142cm或14cm●OABCD1.两条弦在圆心的同侧●OABCD2.两条弦在圆心的两侧 2、⊙O的半径为5cm,弦AB∥CD,
AB=8,CD=6,则AB、CD间的
距离是___ .1cm或7cmEFEF43534154354375小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。垂径定理ED油的最大深度ED=OD-OE=200(mm)或者油的最大深度ED=OD + OE=450(mm).(1) 1在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm,求油的最大深度。OE=125(mm)解:4、⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___ .2cm或14cm 你能利用垂径定理解决求赵州桥拱半径的问题吗?37.4m7.2mABOCD关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦构成直角三角形,便将问题转化为直角三角形的问题。解:如图,用AB表示主桥拱,设AB所在的圆的圆心为O,半径为r.经过圆心O作弦AB的垂线OC垂足为D,与AB交于点C,则D是AB的中点,C是AB的中点,CD就是拱高.∴ AB=37.4m,CD=7.2m∴ AD=1/2 AB=18.7m,OD=OC-CD=r-7.2解得r=27.9(m)即主桥拱半径约为27.9m.⌒⌒
A. 1 B. 2 C. 3 D.无数条
2.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是______cm.A7.OAC.B410?6.一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是______cm.37.OAC.B104? 由此你能得到圆的什么特性? 可以发现:圆是轴对称图形。任何一条直径所在直线都是它的对称轴. 不借助任何工具,你能找到圆形纸片的圆心吗?活动一1、在已有的圆上标出圆心,沿一条直径对折。
2、在对折后的半圆弧上,用笔在同一位置上的正反面做一个标记
3、展开圆,用虚线描出直径,在给标记处表上A、B,并连接AB。ABCDE(1)用量角器确定一下AB与CD的位置关系?(2)AE与BE是什么关系?(3)弦AB所对的弧发生了什么变化?小结:垂直于弦的直径平分弦,
并且平分弦所对的两条弧探究:·OABCDE垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧如图:垂径定理的几个基本图形:BCDAO并用几何语言进行描述下列图形是否具备垂径定理的条件?是不是是不是深化:并用几何语言进行描述ABCDE垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧如图:课堂小结例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径.1巩固:11、如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是( )D、∠COE=∠DOEB、CE=DEC、OE=AE2、如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB= cm。·OABE解:连接OA,∵ OE⊥AB∴ AB=2AE=16cm3、如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。·OABE解:过点O作OE⊥AB于E,连接OA即⊙O的半径为5cm.2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证:四边形ADOE是正方形.·OABCDE证明:∴四边形ADOE为矩形,又 ∵AC=AB,∴ AE=AD.∴ 四边形ADOE为正方形.6.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是 。8cm4.半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是 。5. ⊙O的直径为10cm,圆心O到弦AB的 距离为3cm,则弦AB的长是 。二、填空: 如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE在来!你行吗?解:答:⊙O的半径为5cm.在Rt △ AOE 中 14、如图,CD是⊙O的直径,弦AB⊥CD于E,CE=1,AB=10,求直径CD的长。 2:已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。证明:过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BDE实际上,往往只需从圆心作一条与弦垂直的线段.就可以利用垂径定理来解决有关问题了. 已知:⊙O中弦AB∥CD。
求证:AC=BD⌒⌒.夹在两条平行弦间的弧相等.M●OABCD1.两条弦在圆心的同侧●OABCD2.两条弦在圆心的两侧1、⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___ .EFEF10861068210861086142cm或14cm●OABCD1.两条弦在圆心的同侧●OABCD2.两条弦在圆心的两侧 2、⊙O的半径为5cm,弦AB∥CD,
AB=8,CD=6,则AB、CD间的
距离是___ .1cm或7cmEFEF43534154354375小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。垂径定理ED油的最大深度ED=OD-OE=200(mm)或者油的最大深度ED=OD + OE=450(mm).(1) 1在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm,求油的最大深度。OE=125(mm)解:4、⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___ .2cm或14cm 你能利用垂径定理解决求赵州桥拱半径的问题吗?37.4m7.2mABOCD关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦构成直角三角形,便将问题转化为直角三角形的问题。解:如图,用AB表示主桥拱,设AB所在的圆的圆心为O,半径为r.经过圆心O作弦AB的垂线OC垂足为D,与AB交于点C,则D是AB的中点,C是AB的中点,CD就是拱高.∴ AB=37.4m,CD=7.2m∴ AD=1/2 AB=18.7m,OD=OC-CD=r-7.2解得r=27.9(m)即主桥拱半径约为27.9m.⌒⌒
同课章节目录
