北师大版数学八年级下册第1章第1节等腰三角形(3)学案(表格形式)
文档属性
| 名称 | 北师大版数学八年级下册第1章第1节等腰三角形(3)学案(表格形式) |
|
|
| 格式 | zip | ||
| 文件大小 | 146.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-28 00:00:00 | ||
图片预览

文档简介
北师大版8年级下册第1章第1节等腰三角形(3)学案
课题
1.1等腰三角形(第三课时)
学习目标
1、能够证明等腰三角形的判定定理,并会运用其定理进行证明。2、结合实例体会反证法的含义。3、经历探索、猜想、证明”的过程,进一步发展推理证明意识和能力。
重点难点
等腰三角形的判定定理的证明,结合实例体会反证法的含义.
学
习
过
程
交流预习
预习指导:1、等腰三角形性质定理:(1)等腰三角形的两个 相等,也可以说成 .(2)
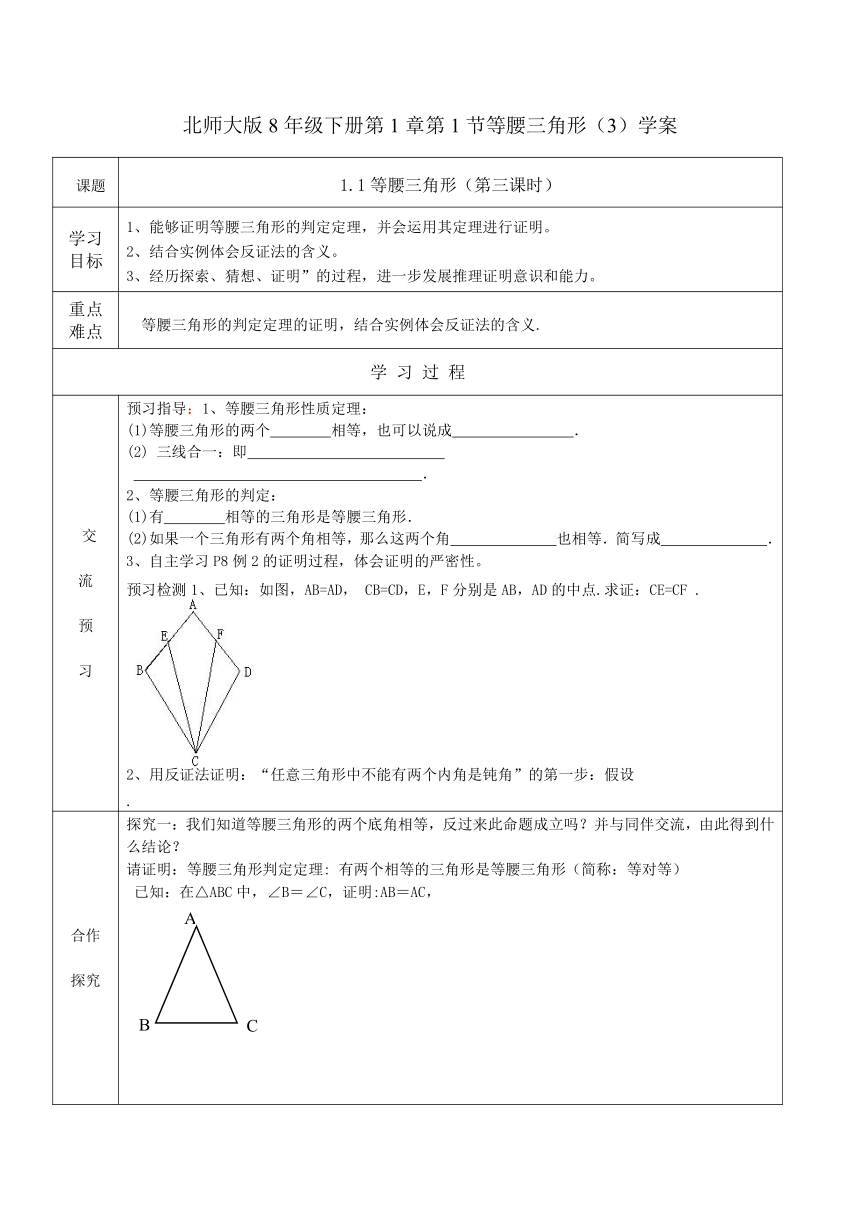
三线合一:即 .2、等腰三角形的判定:(1)有 相等的三角形是等腰三角形.(2)如果一个三角形有两个角相等,那么这两个角 也相等.简写成 .3、自主学习P8例2的证明过程,体会证明的严密性。预习检测1、已知:如图,AB=AD,
CB=CD,E,F分别是AB,AD的中点.求证:CE=CF
.2、用反证法证明:“任意三角形中不能有两个内角是钝角”的第一步:假设.
合作探究
探究一:我们知道等腰三角形的两个底角相等,反过来此命题成立吗?并与同伴交流,由此得到什么结论?请证明:等腰三角形判定定理:
有两个相等的三角形是等腰三角形(简称:等对等)已知:在△ABC中,∠B=∠C,证明:AB=AC,探究二:请同学们阅读课本P8“想一想”,
( http: / / www.21cnjy.com )这一结论成立吗?你能证明吗?若不会证明,请看课本小明是怎样证明的,这种证明问题的方法与以前的证明方法相同吗?若不同应称法.证明步骤:1、假设不成立。2、从这个假设出发,应用正确的推论方法,得出与、
、
或相矛盾的结果。3、由矛盾的结果判定
,从而肯定正确。例:用反证法证明:一个三角形中不能有两个直角。
任务清单
1、在△ABC和△DCB中,AC与BD交于O,
AB=DC
,
AC=BD,求证:△OBC是等腰三角形。2.如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数.3、已知如图,△ABC中AB=AC,点D、E在BC上,∠BAD=∠CAE,求证:△ADE是等腰三角形。2、用反证法证明:一个三角形中至少有一个内角小于或等于60°。已知:求证:
作业
A
B
C
A
B
D
E
C
课题
1.1等腰三角形(第三课时)
学习目标
1、能够证明等腰三角形的判定定理,并会运用其定理进行证明。2、结合实例体会反证法的含义。3、经历探索、猜想、证明”的过程,进一步发展推理证明意识和能力。
重点难点
等腰三角形的判定定理的证明,结合实例体会反证法的含义.
学
习
过
程
交流预习
预习指导:1、等腰三角形性质定理:(1)等腰三角形的两个 相等,也可以说成 .(2)
三线合一:即 .2、等腰三角形的判定:(1)有 相等的三角形是等腰三角形.(2)如果一个三角形有两个角相等,那么这两个角 也相等.简写成 .3、自主学习P8例2的证明过程,体会证明的严密性。预习检测1、已知:如图,AB=AD,
CB=CD,E,F分别是AB,AD的中点.求证:CE=CF
.2、用反证法证明:“任意三角形中不能有两个内角是钝角”的第一步:假设.
合作探究
探究一:我们知道等腰三角形的两个底角相等,反过来此命题成立吗?并与同伴交流,由此得到什么结论?请证明:等腰三角形判定定理:
有两个相等的三角形是等腰三角形(简称:等对等)已知:在△ABC中,∠B=∠C,证明:AB=AC,探究二:请同学们阅读课本P8“想一想”,
( http: / / www.21cnjy.com )这一结论成立吗?你能证明吗?若不会证明,请看课本小明是怎样证明的,这种证明问题的方法与以前的证明方法相同吗?若不同应称法.证明步骤:1、假设不成立。2、从这个假设出发,应用正确的推论方法,得出与、
、
或相矛盾的结果。3、由矛盾的结果判定
,从而肯定正确。例:用反证法证明:一个三角形中不能有两个直角。
任务清单
1、在△ABC和△DCB中,AC与BD交于O,
AB=DC
,
AC=BD,求证:△OBC是等腰三角形。2.如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数.3、已知如图,△ABC中AB=AC,点D、E在BC上,∠BAD=∠CAE,求证:△ADE是等腰三角形。2、用反证法证明:一个三角形中至少有一个内角小于或等于60°。已知:求证:
作业
A
B
C
A
B
D
E
C
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
