第四章一次函数单元检测题

湘教版八年级下册数学第四章一次函数单元检测试题
一、选择题(本大题共10小题)
1. 下列函数是一次函数的是（　　）
A．y=4x2﹣1 B．y=﹣ C．y= D．y=
2. 若关于x的一次函数y=x+3a﹣12的图象与y轴的交点在x轴上方，则a的取值范围是（ ）．【来源：21cnj*y.co*m】
A. a＞4　 B. a<4　 C. a＞3　 D. a<3　
3. 已知P1（﹣1，y1），P2（2，y2）是一次函数y=﹣x+1图象上的两个点，则y1，y2的大小关系是（　　）【出处：21教育名师】
A．y1=y2 B．y1＜y2 C．y1＞y2 D．不能确定
4. 关于直线y=﹣x+1，下列结论正确的是（　　）
A．图象必过点（0，0）
B．直线与坐标轴围成的三角形的面积为0.5
C．图象经过第一、二、三象限
D．y随x的增大而增大
5. 一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（﹣3，0），B（0，2），当函数图象在第二象限时，自变量x的取值范围是（　　）21教育名师原创作品
A．﹣3＜x＜0 B．x＜0 C．﹣3＜x＜2 D．x＞﹣3
6. 一次函数y1=kx+b与y2=x+a的图象如图，则下列结论①k＜0；②a＞0；③当x＜3时，y1＜y2中，正确的个数是（　　）21*cnjy*com
A．0 B．1 C．2 D．3
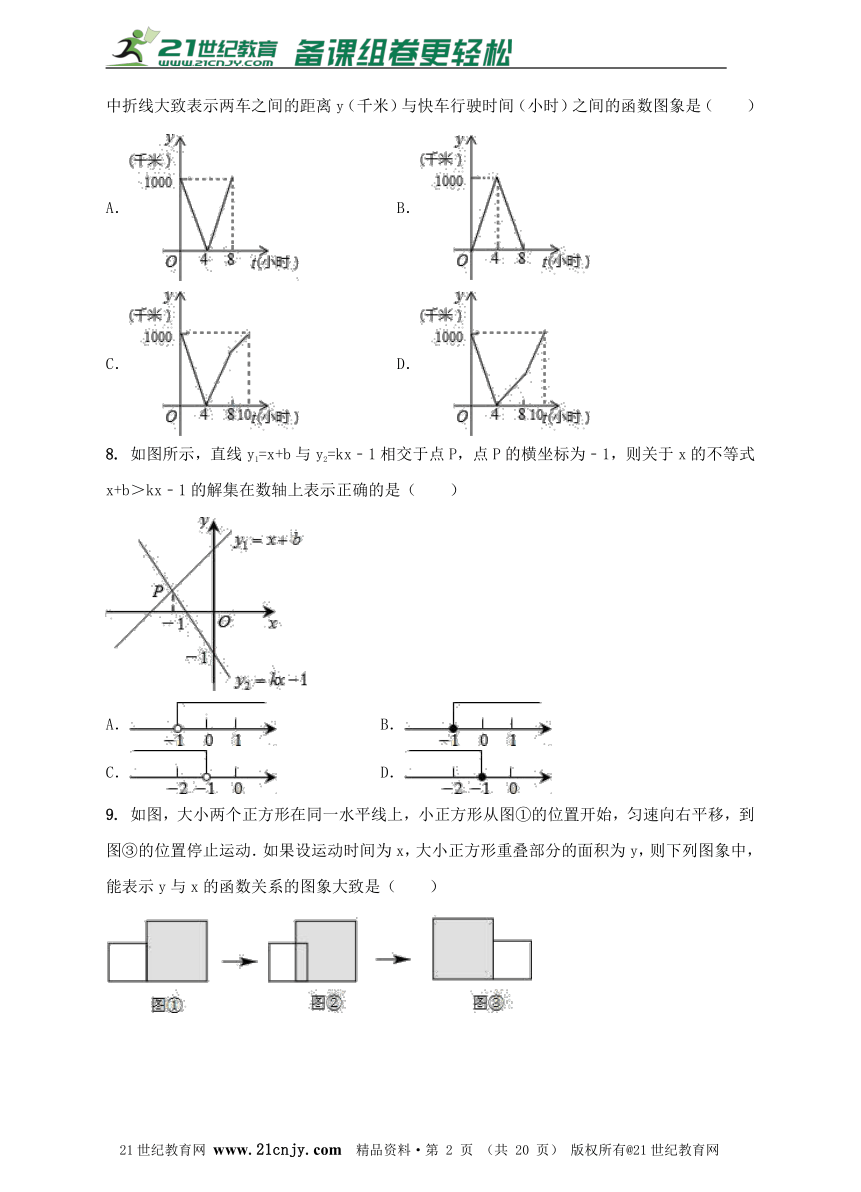
7. 一列快车从甲地驶往乙地，一列特快车从乙地驶往甲地，快车的速度为100千米/小时，特快车的速度为150千米/小时，甲、乙两地之间的距离为1000千米，两车同时出发，则图中折线大致表示两车之间的距离y（千米）与快车行驶时间（小时）之间的函数图象是（　　）
A． B．
C． D．
8. 如图所示，直线y1=x+b与y2=kx﹣1相交于点P，点P的横坐标为﹣1，则关于x的不等式x+b＞kx﹣1的解集在数轴上表示正确的是（　　）
A． B．
C． D．
9. 如图，大小两个正方形在同一水平线上，小正方形从图①的位置开始，匀速向右平移，到图③的位置停止运动．如果设运动时间为x，大小正方形重叠部分的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（　　）【来源：21·世纪·教育·网】
A． B．
C． D．
10. 张师傅驾车从甲地到乙地，两地相距500千米，汽车出发前油箱有油25升，途中加油若干升，加油前、后汽车都以100千米/小时的速度匀速行驶，已知油箱中剩余油量y（升）与行驶时间t（小时）之间的关系如图所示．以下说法错误的是（　　）
A．加油前油箱中剩余油量y（升）与行驶时间t（小时）的函数关系是y=﹣8t+25
B．途中加油21升
C．汽车加油后还可行驶4小时
D．汽车到达乙地时油箱中还余油6升
二、填空题(本大题共8小题)
11. 函数的自变量x的取值范围是　 　．
12. 坐标原点到直线y=2x+4的距离是　　．
13. 直线y=kx+3与y=﹣x+3的图象如图所示，则方程组的解为　 　．
14. 为增强学生体质，某中学在体育课中加强了学生的长跑训练．在一次女子800米耐力测试中，小静和小茜在校园内200米的环形跑道上同时起跑，同时到达终点；所跑的路程S（米）与所用的时间t（秒）之间的函数图象如图所示，则她们第一次相遇的时间是起跑后的第
秒．
15. 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．若直线AB上的点C在第一象限，且S△BOC=2，则点C的坐标是 ．
16. 如图，一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完．假设每分钟的进水量和出水量是两个常数，容器内的水量y（单位：升）与时间x（单位：分）之间的部分关系．那么，从关闭进水管起　　分钟该容器内的水恰好放完．21cnjy.com
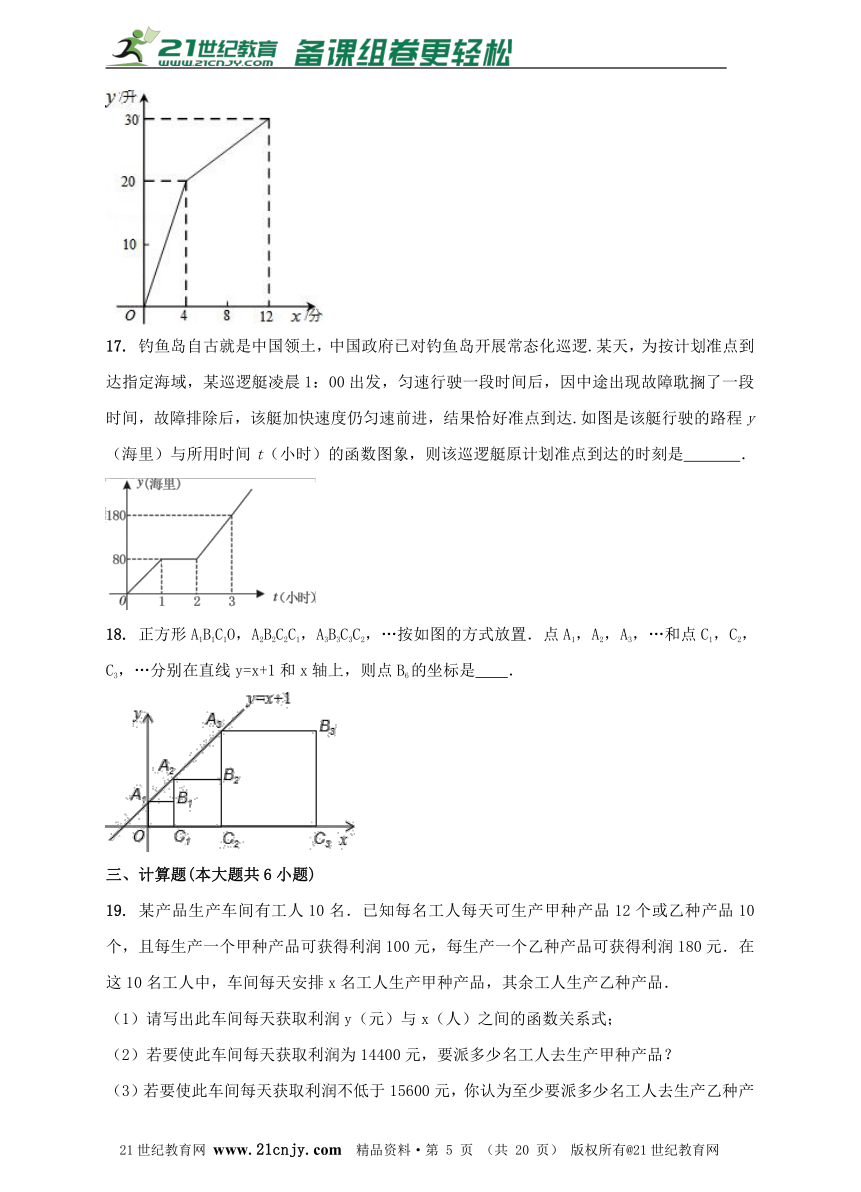
17. 钓鱼岛自古就是中国领土，中国政府已对钓鱼岛开展常态化巡逻.某天，为按计划准点到达指定海域，某巡逻艇凌晨1：00出发，匀速行驶一段时间后，因中途出现故障耽搁了一段时间，故障排除后，该艇加快速度仍匀速前进，结果恰好准点到达.如图是该艇行驶的路程y（海里）与所用时间t（小时）的函数图象，则该巡逻艇原计划准点到达的时刻是 ．
18. 正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点B6的坐标是　　．
三、计算题(本大题共6小题)
19. 某产品生产车间有工人10名．已知每名工人每天可生产甲种产品12个或乙种产品10个，且每生产一个甲种产品可获得利润100元，每生产一个乙种产品可获得利润180元．在这10名工人中，车间每天安排x名工人生产甲种产品，其余工人生产乙种产品．
（1）请写出此车间每天获取利润y（元）与x（人）之间的函数关系式；
（2）若要使此车间每天获取利润为14400元，要派多少名工人去生产甲种产品？
（3）若要使此车间每天获取利润不低于15600元，你认为至少要派多少名工人去生产乙种产品才合适？
20. 如图，已知四边形ABCD是正方形，点B，C分别在两条直线y=2x和y=kx上，点A，D是x轴上两点．21世纪教育网版权所有
（1）若此正方形边长为2，k=　　；
（2）若此正方形边长为a，k的值是否会发生变化？若不会发生变化说明理由；若会发生变化，试求出a的值．www-2-1-cnjy-com
21. 红光运输队欲用A，B，C三种型号的汽车共80辆为某企业一次性将700吨货物从M地运往N地（要求每种型号的汽车都满载），三种型号的汽车的载重量及应获取的运费如表：
汽车型号
A型
B型
C型
载重量（吨）
8
10
12
运费（元）
220
260
280
设派用A型汽车x辆，B型汽车y辆，红光运输队应获取的总运费为w元．
（1）用含x、y的代数式表示派用的C型汽车的辆数　 　；
（2）求y关于x的函数关系式并直接写出x的取值范围；
（3）求w关于x的函数关系式；
（4）若红光运输队获取的总运费为18600元，请问他们的派车方案是怎样的？
22. “五?一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．
（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？2·1·c·n·j·y
23. 一家蔬菜公司收购某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如图所示
销售方式
粗加工后销售
精加工后销售
每吨获利（元）
1000
2000
已知该公司的加工能力是：粗加工每天加工该种蔬菜的重量是精加工的3倍，但两种加工不能同时进行受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售．
（1）若要求15天刚好加工完140吨蔬菜，如果绿色蔬菜先精加工20吨，剩下的再进行粗加工，正好按时完成，求精加工和粗加工每天各能加工的吨数．21*cnjy*com
（2）若要求在13天的时间内，将140吨蔬菜全部加工完，并且两种加工方式都要有，先精加工后粗加工，问哪种分配加工时间（时间取整）的方案利润最大，最大利润是多少？
24. 如图，在平面直角坐标系xOy中，矩形ABCD的AB边在x轴上，AB=3，AD=2，经过点C的直线y=x﹣2与x轴、y轴分别交于点E、F．【版权所有：21教育】
（1）求：①点D的坐标；
②经过点D，且与直线FC平行的直线的函数表达式；
（2）直线y=x﹣2上是否存在点P，使得△PDC为等腰直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．
（3）在平面直角坐标系内确定点M，使得以点M、D、C、E为顶点的四边形是平行四边形，请直接写出点M的坐标．
参考答案：
一、选择题(本大题共10小题)
1. B
分析：依据一次函数的定义求解即可．
解：∵一次函数的一般形式为y=kx+b（k≠0），y=﹣=﹣x，
∴y=﹣是一次函数．
故选：B．
2.A
分析：根据一次函数y=x+3a﹣12的图象与y轴的交点在x轴上方可得出3a﹣12＞0，求出a的取值范围即可．
解：∵一次函数y=x+3a﹣12的图象与y轴的交点在x轴上方，
∴3a﹣12＞0，解得a＞4．故答案为：a＞4．故选A.
3. C
分析：<先根据一次函数y=﹣x+1中k=﹣1判断出函数的增减性，再根据﹣1＜2进行解答即可．
解：∵P1（﹣1，y1）、P2（2，y2）是y=﹣x+1的图象上的两个点，
∴y1=1+1=2，y2=﹣2+1=﹣1，
∵2＞﹣1，
∴y1＞y2．故选C．
4. B
分析：根据题意画出图形即可得到正确答案．
解：画出函数图象：可知三角形的面积为1×1×=，故选B．
5. A
分析：根据点A、B的坐标作出一次函数图象，然后写出x的取值范围即可．
解：函数图象如图所示，函数图象在第二象限时，自变量x的取值范围是﹣3＜x＜0．故选A．
6. B
分析：根据y1=kx+b和y2=x+a的图象可知：k＜0，a＜0，所以当x＜3时，相应的x的值，y1图象均高于y2的图象．
解：∵y1=kx+b的函数值随x的增大而减小，
∴k＜0；故①正确
∵y2=x+a的图象与y轴交于负半轴，
∴a＜0；
当x＜3时，相应的x的值，y1图象均高于y2的图象，
∴y1＞y2，故②③错误．故选：B．
7.C
分析：分三段讨论，①两车从开始到相遇，这段时间两车距迅速减小，②相遇后向相反方向行驶到特快到达甲地，这段时间两车距迅速增加，③特快到达甲地至快车到达乙地，这段时间两车距缓慢增大，结合实际选符合的图象即可．
解：①两车从开始到相遇，这段时间两车距迅速减小；
②相遇后向相反方向行驶到特快到达甲地这段时间两车距迅速增加；
③特快到达甲地至快车到达乙地，这段时间两车距缓慢增大；
结合图象可得C选项符合题意．故选：C．
8. A
分析：首先根据图象可得不等式x+b＞kx﹣1的解集是能是函数y1=x+b的图象在上边的未知数的范围，据此即可求得x的范围，从而判断．
解：不等式x+b＞kx﹣1的解集是x＞﹣1．
则利用数轴表示为
．故选A．
9. C
分析：小正方形运动过程中，y与x的函数关系为分段函数，即当0≤x＜完全重叠前，函数为为增函数；当完全重叠时，函数为平行于x轴的线段；当不再完全重叠时，函数为为减函数．即按照自变量x分为三段．
解：依题意，阴影部分的面积函数关系式是分段函数，
面积由“增加→不变→减少”变化．故选：C．
10. C
分析：A、设加油前油箱中剩余油量y（升）与行驶时间t（小时）的函数关系式为y=kt+b，将（0，25），（2，9）代入，运用待定系数法求解后即可判断；
B、由题中图象即可看出，途中加油量为30﹣9=21升；
C、先求出每小时的用油量，再求出汽车加油后行驶的路程，然后与4比较即可判断；
D、先求出汽车从甲地到达乙地需要的时间，进而得到需要的油量；然后用汽车油箱中原有的油量加上途中的加油量，再减去汽车行驶500千米需要的油量，得出汽车到达乙地时油箱中的余油量即可判断．
解：A、设加油前油箱中剩余油量y（升）与行驶时间t（小时）的函数关系式为y=kt+b．
将（0，25），（2，9）代入，
得，解得，
所以y=﹣8t+25，正确，故本选项不符合题意；
B、由图象可知，途中加油：30﹣9=21（升），正确，故本选项不符合题意；
C、由图可知汽车每小时用油（25﹣9）÷2=8（升），
所以汽车加油后还可行驶：30÷8=3＜4（小时），错误，故本选项符合题意；
D、∵汽车从甲地到达乙地，所需时间为：500÷100=5（小时），
∴5小时耗油量为：8×5=40（升），
又∵汽车出发前油箱有油25升，途中加油21升，
∴汽车到达乙地时油箱中还余油：25+21﹣40=6（升），正确，故本选项不符合题意．
故选C．
二、填空题(本大题共8小题)
11.分析：根据分母不等于0列不等式求解即可．
解：由题意得，x﹣3≠0，
解得x≠3．
故答案为：x≠3．
12.分析：设原点到直线的距离为h，先求出直线与坐标轴的交点，再利用三角形的面积公式求解即可．
解：设原点到直线的距离为h，
∵令x=0，则y=4；令y=0，则x=﹣2，
∴直线与坐标轴的交点为A（0，4），B（﹣2，0），
∴AB==2，
∴2×4=2h，解得h=．
故答案为：．
13. 分析：二元一次方程组的解就是组成二元一次方程组的两个方程的公共解，即两条直线的交点坐标．
解：根据题意知，
二元一次方程组的解就是直线y=kx+3与y=﹣x+3的交点坐标，
又∵交点坐标为（0，3），
∴原方程组的解是：．
故答案为．
14. 分析：分别求出OA、BC的解析式，然后联立方程，解方程就可以求出第一次相遇时间．
解：设直线OA的解析式为y=kx，
代入A（200，800）得800=200k，
解得k=4，
故直线OA的解析式为y=4x，
设BC的解析式为y1=k1x+b，由题意，得，
解得：，
∴BC的解析式为y1=2x+240，
当y=y1时，4x=2x+240，
解得：x=120．
则她们第一次相遇的时间是起跑后的第120秒．
故答案为120．
15. 分析：设直线AB的解析式为y=kx+b，将点A（1，0）、点B（0，﹣2）分别代入解析式即可组成方程组，从而得到AB的解析式；设点C的坐标为（x，y），根据三角形面积公式以及S△BOC=2求出C的横坐标，再代入直线即可求出y的值，从而得到其坐标．
解：设直线AB的解析式为y=kx+b（k≠0），
∵直线AB过点A（1，0）、点B（0，﹣2），
∴，
解得，
∴直线AB的解析式为y=2x﹣2．
设点C的坐标为（x，y），
∵S△BOC=2，
∴?2?x=2，
解得x=2，
∴y=2×2﹣2=2，
∴点C的坐标是（2，2）．
16. 分析：先根据函数图象求出进水管的进水量和出水管的出水量，由工程问题的数量关系就可以求出结论．
解：由函数图象得：
进水管每分钟的进水量为：20÷4=5升
设出水管每分钟的出水量为a升，由函数图象，得
20+8（5﹣a）=30，
解得：a=，
故关闭进水管后出水管放完水的时间为：30÷=8分钟．
故答案为：8．
17. 分析：本题考查函数图象的意义，列一元一次方程解实际问题．解答时，一要由函数图象判断巡逻艇故障前、后的速度；二要理解“结果恰好准时到达”蕴涵的等量关系：按故障前速度行驶全程所用时间＝2＋按故障排除后速度行驶剩余路程所用时间．
解：观察函数图象，知巡逻艇出现故障前的速度为：80÷1=80海里/小时，故障排除后的速度为：(180－80)÷1=100海里/小时．
设巡逻艇的航行全程为x海里，由题意，得＝2＋，解得x＝480．
则原计划行驶的时间为：480÷80＝6（小时）．
故计划准点到达的时刻为7：00．
18. 分析：首先利用直线的解析式，分别求得A1，A2，A3，A4…的坐标，由此得到一定的规律，据此求出点An的坐标，即可得出点B6的坐标．
解：∵直线y=x+1，x=0时，y=1，
∴A1B1=1，点B2的坐标为（3，2），
∴A1的纵坐标是：1=20，A1的横坐标是：0=20﹣1，
∴A2的纵坐标是：1+1=21，A2的横坐标是：1=21﹣1，
∴A3的纵坐标是：2+2=4=22，A3的横坐标是：1+2=3=22﹣1，
∴A4的纵坐标是：4+4=8=23，A4的横坐标是：1+2+4=7=23﹣1，
即点A4的坐标为（7，8）．
据此可以得到An的纵坐标是：2n﹣1，横坐标是：2n﹣1﹣1．
即点An的坐标为（2n﹣1﹣1，2n﹣1）．
∴点A6的坐标为（25﹣1，25）．
∴点B6的坐标是：（26﹣1，25）即（63，32）．
故答案为：（63，32）．
三、计算题(本大题共6小题)
19. 分析：（1）根据每个工人每天生产的产品个数以及每个产品的利润，表示出总利润即可；
（2）根据每天获取利润为14400元，则y=14400，求出即可；
（3）根据每天获取利润不低于15600元即y≥15600，求出即可．
解：（1）根据题意得出：
y=12x×100+10（10﹣x）×180
=﹣600x+18000；
（2）当y=14400时，有14400=﹣600x+18000，
解得：x=6，
故要派6名工人去生产甲种产品；
（3）根据题意可得，
y≥15600，
即﹣600x+18000≥15600，
解得：x≤4，
则10﹣x≥6，
故至少要派6名工人去生产乙种产品才合适．
20. 分析：根据正方形的边长，运用正方形的性质表示出C点的坐标，再将C的坐标代入函数中，从而可求得k的值．21教育网
解：（1）∵正方形边长为2，
∴AB=2，
在直线y=2x中，当y=2时，x=1，
∴OA=1，OD=1+2=3，
∴C（3，2），
将C（3，2）代入y=kx，得2=3k，
∴k=；
故答案为：；
（2）k的值不会发生变化，
理由：∵正方形边长为a，
∴AB=a，
在直线y=2x中，当y=a时，x=，
∴OA=，OD=，
∴C（，a），
将C（，a）代入y=kx，得a=k×，
∴k=．
21. 分析：（1）根据题意得出C型货车的辆数即可；
（2）根据题意列出y关于x的函数关系式，再根据y≥0即可求出符合条件的未知数的对应值；
（3）根据题意列出w关于x的函数关系式即可；
（4）根据红光运输队获取的总运费为18600元，得出x的值，得出方案即可．
解：（1）设派用A型汽车x辆，B型汽车y辆，C型货车的辆数为（80﹣x﹣y）；
故答案为：（80﹣x﹣y）；
（2）根据题意，可得：8x+10y+12（80﹣x﹣y）=700，
解得：y=130﹣2x，
可得：x的取值范围50≤x≤65；
（3）设派用A型汽车x辆，红光运输队应获取的总运费为w元，可得：
w=220x+260+280[80﹣x﹣]=19800﹣20x；
（4）根据题意可得：19800﹣20x=18600，
解得：x=60，
派车方案为A型汽车60辆，B型汽车10辆，C型汽车10辆．
22. 分析：（1）根据原有的人数﹣a分钟检票额人数+a分钟增加的人数=520建立方程求出其解就可以；21·cn·jy·com
（2）设当10≤x≤30时，y与x之间的函数关系式为y=kx+b，由待定系数法求出函数的解析式，再将x=20代入解析式就可以求出结论；www.21-cn-jy.com
（3）设需同时开放n个检票口，根据原来的人数+15分进站人数≥n个检票口15分钟检票人数建立不等式，求出其解即可21·世纪*教育网
解：（1）由图象知，640+16a﹣2×14a=520，
∴a=10；
（2）设当10≤x≤30时，y与x之间的函数关系式为y=kx+b，由题意，得
，
解得：，
y=﹣26x+780，当x=2时，
y=260
即检票到第20分钟时，候车室排队等候检票的旅客有260人．
（3）设需同时开放n个检票口，则由题意知
14n×15≥640+16×15
解得：n≥4，
∵n为整数，
∴n=5．
答：至少需要同时开放5个检票口．
23. 分析：（1）本题等量关系为：精加工天数+粗加工天数=15，进而列出方程求解即可．
（2）首先求出精加工的天数的取值范围，然后表示W并求出W最大值．
解：（1）设每天精加工x吨，则每天粗加工3x吨，依题意得，
+=15，
解得：x=4，
经检验得：x=4是原方程的根；
则3x=12，
答：每天精加工4吨，则每天粗加工12吨；
（2）设精加工的时间为m天，依题意得m+≤13，
解得：m≤2，
设加工这批蔬菜可获利W元，则
W=2000?4m+1000?=140000+4000m（元）（0≤m≤2），
由一次函数性质知，W随m的增大而增大，
故当m=2时，W取得最大值为140000+4000×2=148000（元），
答：安排2天进行精加工，11天粗加工可获最大利润为148000元．
24. 分析：（1）①设点C的坐标为（m，2），根据一次函数图象上点的坐标特征，代入直线解析式求解即可得到m的值，再根据矩形的长求出OA，然后写出点D的坐标即可；
②根据互相平行的直线的解析式的k值相等设出直线解析式为y=x+b，然后把点D的坐标代入函数解析式求解即可；2-1-c-n-j-y
（2）根据直线解析式求出△EBC为等腰直角三角形，根据等腰直角三角形的性质可得∠CEB=∠ECB=45°，再根据平行线的性质可得∠DCE=∠CEB=45°，然后判断出△PDC只能是以P、D为直角顶点的等腰直角三角形，再分①∠D=90°时，根据点P的横坐标与点D的横坐标相等，利用直线解析式求解即可；②∠DPC=90°时，作DC的垂直平分线与直线y=x﹣2的交点即为点P2，求出点P的横坐标，再代入直线解析式计算即可得解；
（3）根据平行四边形平行且对边相等，分DE、CE是对角线时，点M在x轴上，求出OM的长度，然后写出点M的坐标，CD是对角线时，求出平行四边形的中心的坐标，再求出点E关于中心的对称点，即为点M．
解：（1）①设点C的坐标为（m，2），
∵点C在直线y=x﹣2上，
∴2=m﹣2，
∴m=4，
即点C的坐标为（4，2），
∵四边形ABCD是矩形，
∴AB=CD=3，AD=BC=2，
∴点D的坐标为（1，2）；
②设经过点D且与FC平行的直线函数表达式为y=x+b，
将D（1，2）代入y=x+b，得b=1，
∴经过点D且与FC平行的直线函数表达式为y=x+1；
（2）存在．
∵△EBC为等腰直角三角形，
∴∠CEB=∠ECB=45°，
又∵DC∥AB，
∴∠DCE=∠CEB=45°，
∴△PDC只能是以P、D为直角顶点的等腰直角三角形，
如图，①当∠D=90°时，延长DA与直线y=x﹣2交于点P1，
∵点D的坐标为（1，2），
∴点P1的横坐标为1，
把x=1代入y=x﹣2得，y=﹣1，
∴点P1（1，﹣1）；
②当∠DPC=90°时，作DC的垂直平分线与直线y=x﹣2的交点即为点P2，
所以，点P2的横坐标为=，
把x=代入y=x﹣2得，y=，
所以，点P2（，），
综上所述，符合条件的点P的坐标为（1，﹣1）或（，）；
（3）当y=0时，x﹣2=0，
解得x=2，
∴OE=2，
∵以点M、D、C、E为顶点的四边形是平行四边形，
∴若DE是对角线，则EM=CD=3，
∴OM=EM﹣OE=3﹣2=1，
此时，点M的坐标为（﹣1，0），
若CE是对角线，则EM=CD=3，
OM=OE+EM=2+3=5，
此时，点M的坐标为（5，0），
若CD是对角线，则平行四边形的中心坐标为（，2），
设点M的坐标为（x，y），
则=， =2，
解得x=3，y=4，
此时，点M的坐标为（3，4），
综上所述，点M的坐标为（﹣1，0），（5，0）（3，4）．