18.1.1 平行四边形的性质(带解析)
文档属性
| 名称 | 18.1.1 平行四边形的性质(带解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 561.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-29 18:10:34 | ||
图片预览


文档简介
18.1.1平行四边形的性质(带解析)
一、选择题
1.在平行四边形ABCD中,∠A+∠C=120°,则∠B的度数为( )
A.40° B.60° C.100° D.120°
2.在?ABCD中,对角线AC和BD相交于点O,如果AC=10,BD=12,AB=m,那么m的取值范围是( )【来源:21cnj*y.co*m】
A.2<m<22 B.1<m<11 C.10<m<12 D.5<m<6
图1 图2 图3
3.如图1,在平行四边形ABCD中,CE⊥AB且E为垂足.如果∠A=125°,则∠BCE=( )
A.55° B.35° C.25° D.30°
4.如图2,平行四边形ABCD中,经过对角线交点O的直线分别交AB、CD于点E、F.则图中全等的三角形共有( ),【来源:21·世纪·教育·网】
A.4对 B.5对 C.6对 D.8对
5.如图3所示,在?ABCD中,对角线AC、BD相交于点O,且AB≠AD,则下列式子不正确的是( )【出处:21教育名师】
A.AC⊥BD B.AB=CD C.BO=OD D.∠BAD=∠BCD
图4 图5 图6
6.如图4,?ABCD不具有的性质是( ),
A.ABCD B.AO=OC C.AC=BD D.∠BAD=∠BCD
7.如图5,在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=( )www.21-cn-jy.com
A.110° B.30° C.50° D.70°
二、填空题
8.在平行四边形ABCD中,若∠A+∠C=210°,则∠B=?? ? .
9.平行四边形的长边是短边的2倍,一条对角线与短边互相垂直,则这个平行四边形的一个锐角为??? .21cnjy.com
10.如图6,在?ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC+BD=??? .2·1·c·n·j·y
11.如图7,在面积为18的平行四边形ABCD中,AB=6,AD=9,DE⊥AB,DF⊥BC,垂足分别为点E、F,那么BE+BF的值为??? .(结果保留根号)【版权所有:21教育】
图7
三、解答题
12.已知:如图,四边形ABCD是平行四边形,E、F是直线BD上的两点,且DE=BF,求证:AE=CF.21教育名师原创作品
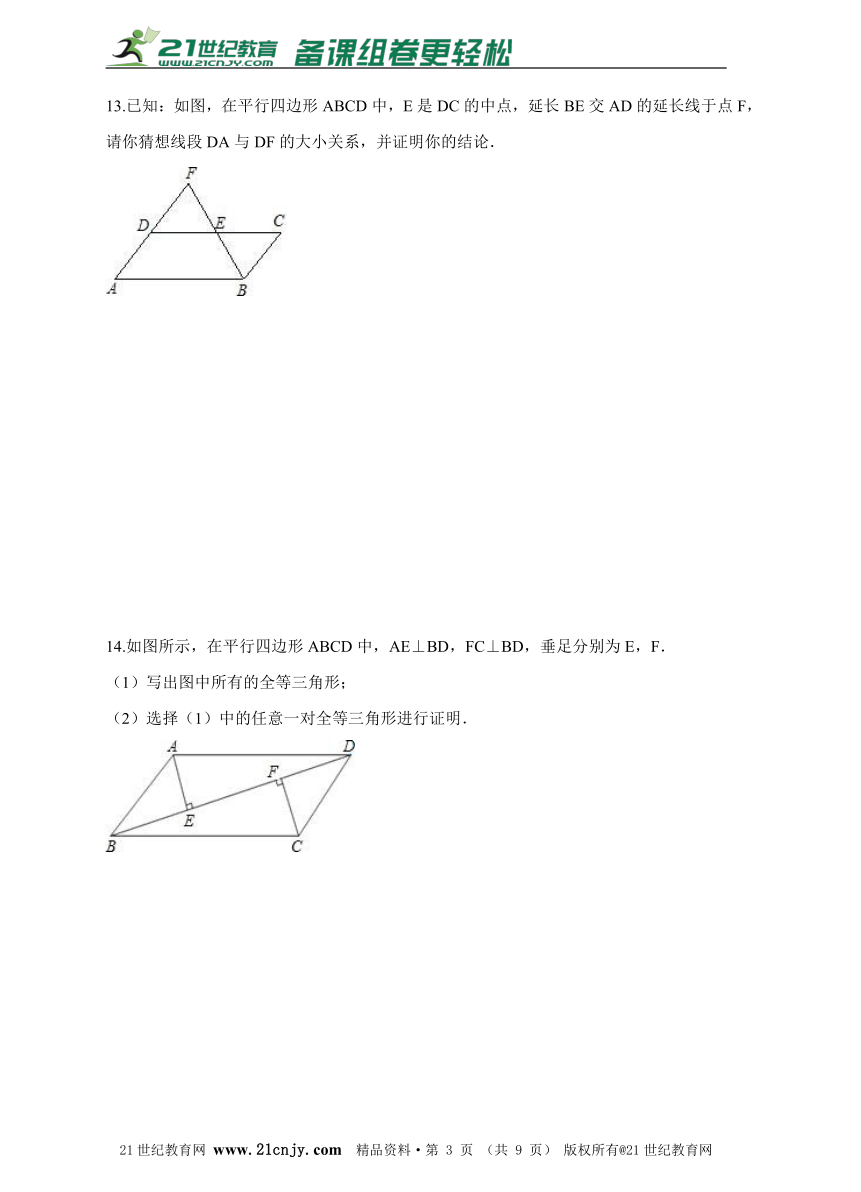
13.已知:如图,在平行四边形ABCD中,E是DC的中点,延长BE交AD的延长线于点F,请你猜想线段DA与DF的大小关系,并证明你的结论.21世纪教育网版权所有
14.如图所示,在平行四边形ABCD中,AE⊥BD,FC⊥BD,垂足分别为E,F. (1)写出图中所有的全等三角形; (2)选择(1)中的任意一对全等三角形进行证明.21教育网
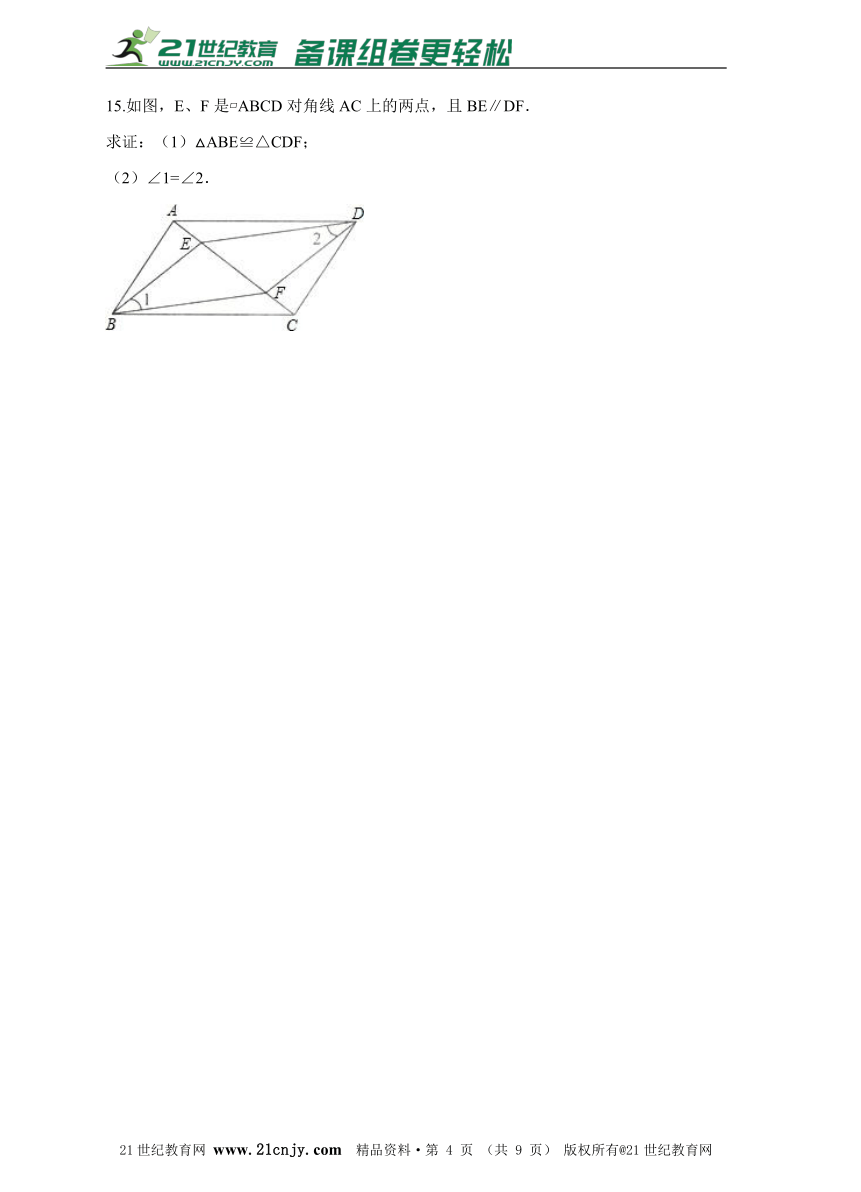
15.如图,E、F是?ABCD对角线AC上的两点,且BE∥DF. 求证:(1)△ABE≌△CDF; (2)∠1=∠2.21·cn·jy·com
参考答案及解析
1.D 【解析】∵四边形ABCD是平行四边形, ∴∠A=∠C,∠A+∠B=180°, ∵∠A+∠C=120°, ∴∠A=60°, ∴∠B=180°-60°=120°. 2.B 【解析】21·世纪*教育网
∵四边形ABCD是平行四边形,AC=10,BD=12, ∠OAB=∠OCD,∠OBD=∠ODC; ①∵AD=BC,AB=CD,BD=BD, ∴△ABD≌△CDB(SSS);同理可证得:△ABC≌△CDA. ②∵OA=OC,OB=OD,AB=CD, ∴△OAB≌△OCD(SSS);同理可证得:△OAD≌△OCB. ③∵OA=OC,∠OAB=∠OCD,∠AOE=∠COF, ∴△AOE≌△COF(ASA);同理可证得:△BOE≌△DOF. 所以图中共有6对全等三角形. 5.A 【解析】∵四边形ABCD为平行四边形, ∴AB=CD,则选项B正确; 又根据平行四边形的对角线互相平分, ∴BO=OD,则选项C正确; 又∵四边形ABCD为平行四边形, www-2-1-cnjy-com
∴∠A=∠ADE=180°-∠B=70° ∵∠E+∠F=∠ADE ∴∠E+∠F=70° 8.75° 【解析】∵平行四边形ABCD, ∴∠A+∠B=180°, ∵∠A+∠C=210°, ∴∠A=∠C=105°, ∴∠B=75°. 9.60° 【解析】2-1-c-n-j-y
∵AC⊥AB, ∴∠BAC=90°, ∵BC=2AB, ∴∠ACB=30°, ∴∠B=60°. ∴这个平行四边形的一个锐角为60°. 10.18 12.见解析 【解析】证明:∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC, ∴∠ADB=∠CBD. ∵∠EDA+∠ADB=180°,∠FBC+∠CBD=180°, ∴∠EDA=∠FBC, ∴△ADE≌△CBF. ∴AE=CF. 13.见解析 【解析】DA=DF. ∵四边形ABCD是平行四边形, ∴AD∥CB,AD=CB, ∴∠F=∠FBC, 而∠FED=∠BEC, 又E是DC的中点,
②证明△ABE≌△CDF. 证明:∵AE⊥BD,CF⊥BD, ∴∠AEB=∠CFD=90°. ∵ABCD是平行四边形, ∴AB∥CD且AB=CD. ∴∠ABE=∠CDF. ∴△ABE≌△CDF. ③证明△AED≌△CFB. 证明:∵AE⊥BD,CF⊥BD, ∴∠AED=∠CFB=90°. ∵ABCD是平行四边形, ∴AD∥CB且AD=CB. ∴∠ADE=∠CBF. ∴△AED≌△CFB. 15.见解析21*cnjy*com
∴四边形BEDF是平行四边形 ∴∠1=∠2.
一、选择题
1.在平行四边形ABCD中,∠A+∠C=120°,则∠B的度数为( )
A.40° B.60° C.100° D.120°
2.在?ABCD中,对角线AC和BD相交于点O,如果AC=10,BD=12,AB=m,那么m的取值范围是( )【来源:21cnj*y.co*m】
A.2<m<22 B.1<m<11 C.10<m<12 D.5<m<6
图1 图2 图3
3.如图1,在平行四边形ABCD中,CE⊥AB且E为垂足.如果∠A=125°,则∠BCE=( )
A.55° B.35° C.25° D.30°
4.如图2,平行四边形ABCD中,经过对角线交点O的直线分别交AB、CD于点E、F.则图中全等的三角形共有( ),【来源:21·世纪·教育·网】
A.4对 B.5对 C.6对 D.8对
5.如图3所示,在?ABCD中,对角线AC、BD相交于点O,且AB≠AD,则下列式子不正确的是( )【出处:21教育名师】
A.AC⊥BD B.AB=CD C.BO=OD D.∠BAD=∠BCD
图4 图5 图6
6.如图4,?ABCD不具有的性质是( ),
A.ABCD B.AO=OC C.AC=BD D.∠BAD=∠BCD
7.如图5,在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=( )www.21-cn-jy.com
A.110° B.30° C.50° D.70°
二、填空题
8.在平行四边形ABCD中,若∠A+∠C=210°,则∠B=?? ? .
9.平行四边形的长边是短边的2倍,一条对角线与短边互相垂直,则这个平行四边形的一个锐角为??? .21cnjy.com
10.如图6,在?ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC+BD=??? .2·1·c·n·j·y
11.如图7,在面积为18的平行四边形ABCD中,AB=6,AD=9,DE⊥AB,DF⊥BC,垂足分别为点E、F,那么BE+BF的值为??? .(结果保留根号)【版权所有:21教育】
图7
三、解答题
12.已知:如图,四边形ABCD是平行四边形,E、F是直线BD上的两点,且DE=BF,求证:AE=CF.21教育名师原创作品
13.已知:如图,在平行四边形ABCD中,E是DC的中点,延长BE交AD的延长线于点F,请你猜想线段DA与DF的大小关系,并证明你的结论.21世纪教育网版权所有
14.如图所示,在平行四边形ABCD中,AE⊥BD,FC⊥BD,垂足分别为E,F. (1)写出图中所有的全等三角形; (2)选择(1)中的任意一对全等三角形进行证明.21教育网
15.如图,E、F是?ABCD对角线AC上的两点,且BE∥DF. 求证:(1)△ABE≌△CDF; (2)∠1=∠2.21·cn·jy·com
参考答案及解析
1.D 【解析】∵四边形ABCD是平行四边形, ∴∠A=∠C,∠A+∠B=180°, ∵∠A+∠C=120°, ∴∠A=60°, ∴∠B=180°-60°=120°. 2.B 【解析】21·世纪*教育网
∵四边形ABCD是平行四边形,AC=10,BD=12, ∠OAB=∠OCD,∠OBD=∠ODC; ①∵AD=BC,AB=CD,BD=BD, ∴△ABD≌△CDB(SSS);同理可证得:△ABC≌△CDA. ②∵OA=OC,OB=OD,AB=CD, ∴△OAB≌△OCD(SSS);同理可证得:△OAD≌△OCB. ③∵OA=OC,∠OAB=∠OCD,∠AOE=∠COF, ∴△AOE≌△COF(ASA);同理可证得:△BOE≌△DOF. 所以图中共有6对全等三角形. 5.A 【解析】∵四边形ABCD为平行四边形, ∴AB=CD,则选项B正确; 又根据平行四边形的对角线互相平分, ∴BO=OD,则选项C正确; 又∵四边形ABCD为平行四边形, www-2-1-cnjy-com
∴∠A=∠ADE=180°-∠B=70° ∵∠E+∠F=∠ADE ∴∠E+∠F=70° 8.75° 【解析】∵平行四边形ABCD, ∴∠A+∠B=180°, ∵∠A+∠C=210°, ∴∠A=∠C=105°, ∴∠B=75°. 9.60° 【解析】2-1-c-n-j-y
∵AC⊥AB, ∴∠BAC=90°, ∵BC=2AB, ∴∠ACB=30°, ∴∠B=60°. ∴这个平行四边形的一个锐角为60°. 10.18 12.见解析 【解析】证明:∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC, ∴∠ADB=∠CBD. ∵∠EDA+∠ADB=180°,∠FBC+∠CBD=180°, ∴∠EDA=∠FBC, ∴△ADE≌△CBF. ∴AE=CF. 13.见解析 【解析】DA=DF. ∵四边形ABCD是平行四边形, ∴AD∥CB,AD=CB, ∴∠F=∠FBC, 而∠FED=∠BEC, 又E是DC的中点,
②证明△ABE≌△CDF. 证明:∵AE⊥BD,CF⊥BD, ∴∠AEB=∠CFD=90°. ∵ABCD是平行四边形, ∴AB∥CD且AB=CD. ∴∠ABE=∠CDF. ∴△ABE≌△CDF. ③证明△AED≌△CFB. 证明:∵AE⊥BD,CF⊥BD, ∴∠AED=∠CFB=90°. ∵ABCD是平行四边形, ∴AD∥CB且AD=CB. ∴∠ADE=∠CBF. ∴△AED≌△CFB. 15.见解析21*cnjy*com
∴四边形BEDF是平行四边形 ∴∠1=∠2.
