数学四年级下西师大版2乘法运算定律课件(18张)
文档属性
| 名称 | 数学四年级下西师大版2乘法运算定律课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-29 00:00:00 | ||
图片预览




文档简介
课件18张PPT。
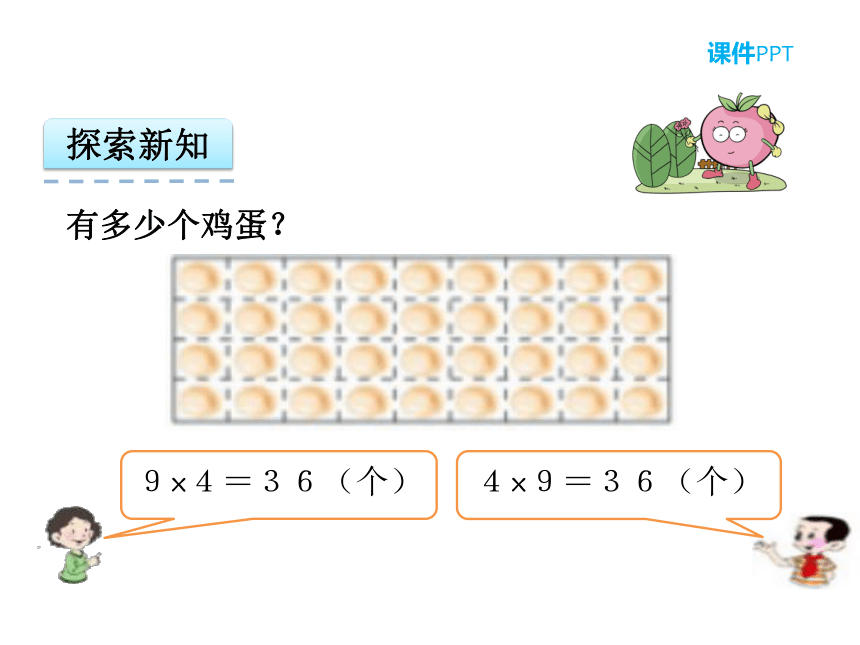
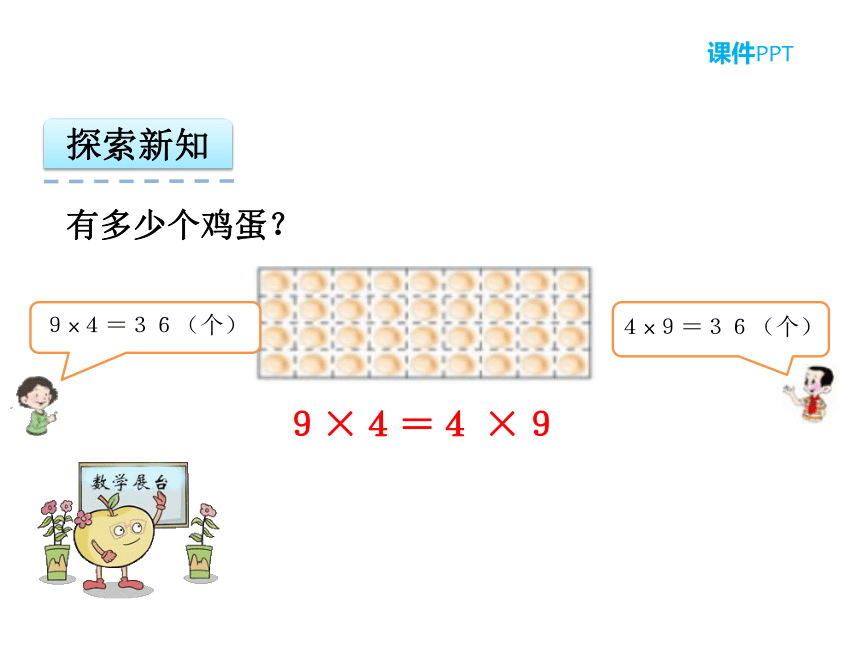
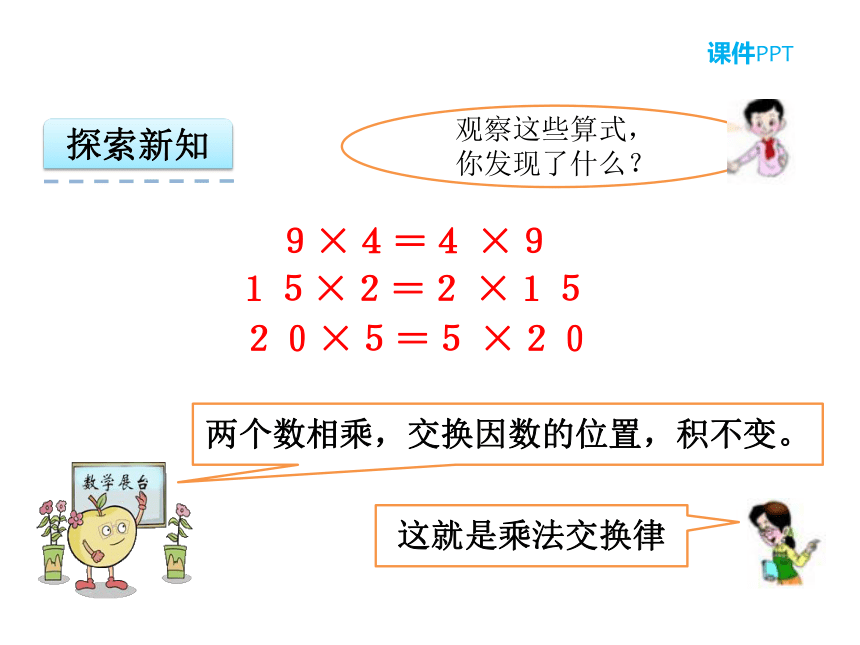
2.2 乘法运算定律第2单元 乘除法的关系和乘法运算律 1.经历在计算和解决问题的具体情景中探索、发现乘法交换律、结合律的过程。2. 理解并掌握乘法交换律和结合律,初步能用这两个运算律解释计算的理由。情景导入有多少个鸡蛋?探索新知有多少个鸡蛋?有多少个鸡蛋?9×4=4 ×9探索新知9×4=4 ×9写出几个有这种规律的算式。15×2=2 ×1520×5=5 ×20……探索新知9×4=4 ×915×2=2 ×1520×5=5 ×20两个数相乘,交换因数的位置,积不变。探索新知 a×b=b×a如果用a和b表示两个数,乘法交换律可以表示为:探索新知这个小区共有多少户?探索新知这个小区共有多少户?6×24 × 8=6×(24 × 8)
探索新知16×5×2= 35 × 25 × 4= 12 × (125 × 8)= 16×(5 ×2)= 35 ×(25 × 4)= 12 × 125 × 8= 算一算。探索新知3个数相乘,先把前两个数相乘,再乘第3个数;或先把后两个数相乘,再乘第1个数,积不变。这就是乘法结合律。如果用a,b,c表示3个数,乘法结合律可以表示为: (a×b)× c=a×(b×c)探索新知1. 两个数相乘,交换因数的位置,( )不变,这就是乘法( )。用字母表示为( )
2. 3个数相乘,先把前两个数相乘,再乘第3个数,或先把后两个相乘,再乘第1个数,( )不变,这就是乘法( )。用字母表示为( )
积交换律 a×b=b×a积结合律 (a×b)× c=a×(b×c)学以致用根据算式,说出运算定律。12×10=10×1246×4=4×46
(35×4)×25=35×(4×25)8×(75×125)= (8×125)×75学以致用先计算,再利用乘法交换律验算。56×32140×25
易错提醒根据运算律,在下面的 里填 上适当的数。4×24=24×(75×4)×25= 75×(4× )46× = ×25
(58× )×20= ×(5×20)4252546558学以致用(44+56)+28 125 × 8 × 11
30 × 16 44+28+56
4 × 27 × 25 16 × 30
88 × 125 27 × (4 × 25)
把左右两边结果相等的算式用线连起来。今天这节课,
你都学到了什么?
你还有什么问题?
2.2 乘法运算定律第2单元 乘除法的关系和乘法运算律 1.经历在计算和解决问题的具体情景中探索、发现乘法交换律、结合律的过程。2. 理解并掌握乘法交换律和结合律,初步能用这两个运算律解释计算的理由。情景导入有多少个鸡蛋?探索新知有多少个鸡蛋?有多少个鸡蛋?9×4=4 ×9探索新知9×4=4 ×9写出几个有这种规律的算式。15×2=2 ×1520×5=5 ×20……探索新知9×4=4 ×915×2=2 ×1520×5=5 ×20两个数相乘,交换因数的位置,积不变。探索新知 a×b=b×a如果用a和b表示两个数,乘法交换律可以表示为:探索新知这个小区共有多少户?探索新知这个小区共有多少户?6×24 × 8=6×(24 × 8)
探索新知16×5×2= 35 × 25 × 4= 12 × (125 × 8)= 16×(5 ×2)= 35 ×(25 × 4)= 12 × 125 × 8= 算一算。探索新知3个数相乘,先把前两个数相乘,再乘第3个数;或先把后两个数相乘,再乘第1个数,积不变。这就是乘法结合律。如果用a,b,c表示3个数,乘法结合律可以表示为: (a×b)× c=a×(b×c)探索新知1. 两个数相乘,交换因数的位置,( )不变,这就是乘法( )。用字母表示为( )
2. 3个数相乘,先把前两个数相乘,再乘第3个数,或先把后两个相乘,再乘第1个数,( )不变,这就是乘法( )。用字母表示为( )
积交换律 a×b=b×a积结合律 (a×b)× c=a×(b×c)学以致用根据算式,说出运算定律。12×10=10×1246×4=4×46
(35×4)×25=35×(4×25)8×(75×125)= (8×125)×75学以致用先计算,再利用乘法交换律验算。56×32140×25
易错提醒根据运算律,在下面的 里填 上适当的数。4×24=24×(75×4)×25= 75×(4× )46× = ×25
(58× )×20= ×(5×20)4252546558学以致用(44+56)+28 125 × 8 × 11
30 × 16 44+28+56
4 × 27 × 25 16 × 30
88 × 125 27 × (4 × 25)
把左右两边结果相等的算式用线连起来。今天这节课,
你都学到了什么?
你还有什么问题?
