山东省滨州市惠民县2016-2017学年九年级数学下学期第一次月考试题(含答案)
文档属性
| 名称 | 山东省滨州市惠民县2016-2017学年九年级数学下学期第一次月考试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 132.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-30 00:00:00 | ||
图片预览



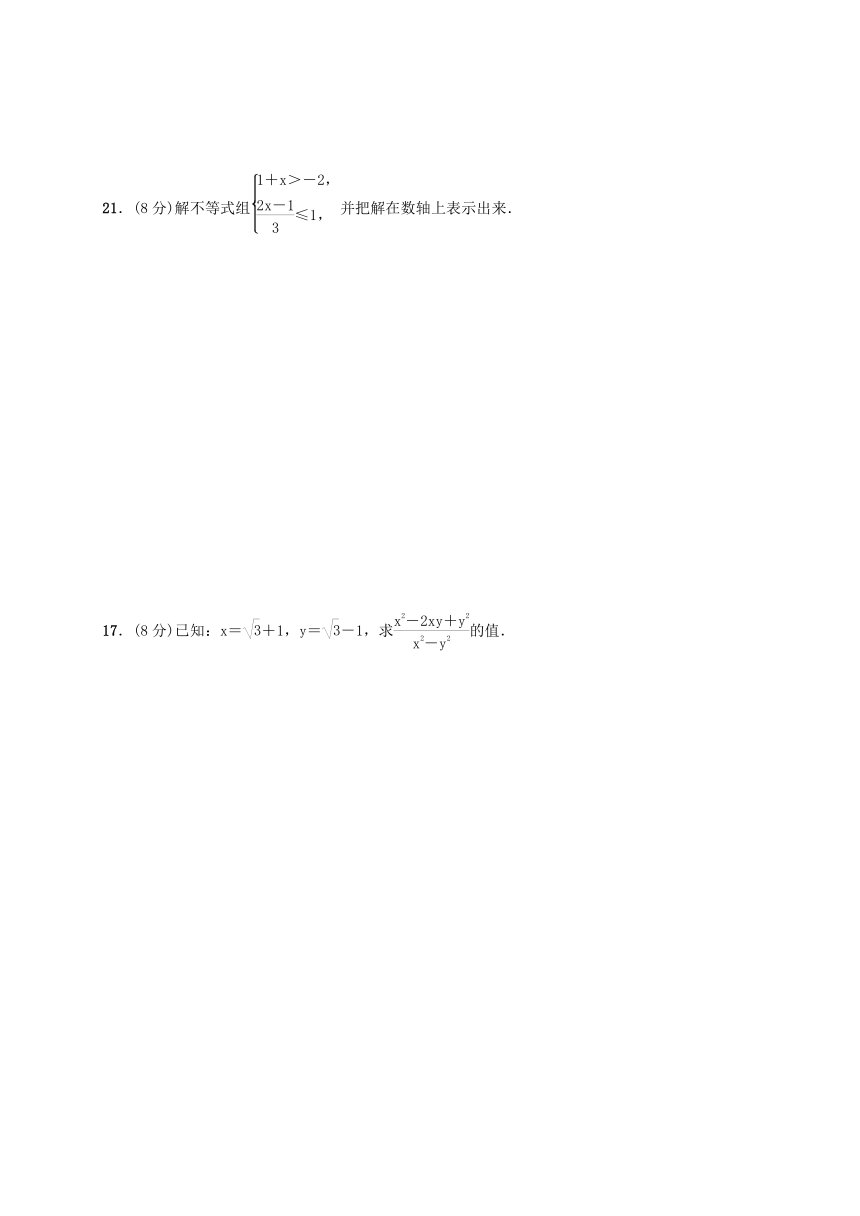
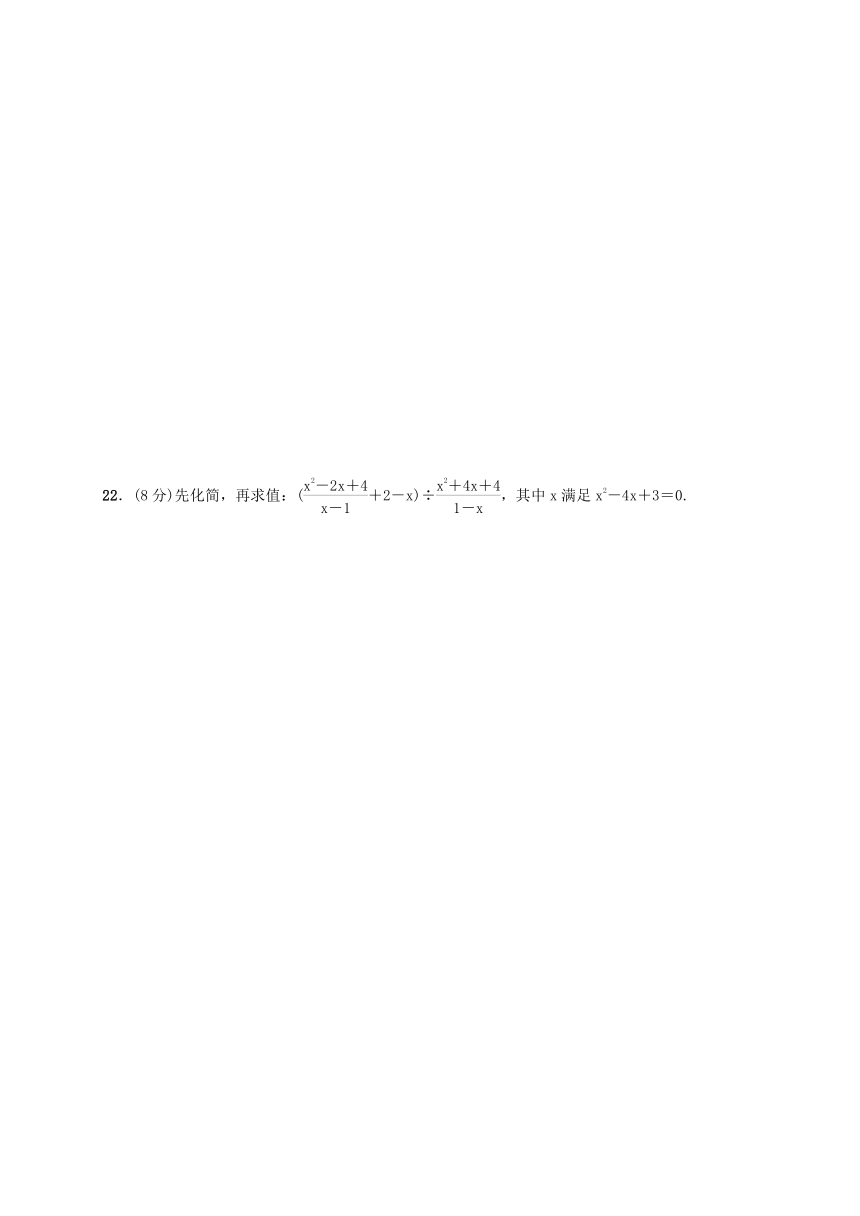
文档简介
九年级数学月检测试题
一、选择题(每小题3分,共36分)
1.下列四个实数中,绝对值最小的数是(
)
A.-5
B.-
C.1
D.4
2.据某省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜旅客约27
700
000人,将27
700
000用科学记数法表示为(
)
A.0.277×107
B.0.277×108
C.2.77×107
D.2.77×108
3.如图,数轴上的点A、B分别对应实数a、b,下列结论正确的是(
)
A.a>b
B.|a|>|b|
C.-aD.a+b<0
4.下列运算正确的是(
)
A.2a3÷a=6
B.(ab2)2=ab4
C.(a+b)(a-b)=a2-b2
D.(a+b)2=a2+b2
5.已知实数x,y满足+(y+1)2=0,则x-y等于(
A
)
A.3
B.-3
C.1
D.-1
6.方程3x+2(1-x)=4的解是(
)
A.x=
B.x=
C.x=2
D.x=1
7.二元一次方程组的解是(
)
A.
B.
C.
D.
8.一元一次不等式2(x+2)≥6的解在数轴上表示为(
)
9.下列方程有两个相等的实数根的是(
)
A.x2+x+1=0
B.4x2+x+1=0
C.x2+12x+36=0
D.x2+x-2=0
10.已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是(
)
A.5
B.7
C.5或7
D.10
11.若关于x的一元一次不等式组有解,则m的取值范围为(
)
A.m>-
B.m≤
C.m>
D.m≤-
12.某校为了丰富学生的校园生活,准备购买一批陶笛,已知A型陶笛比B型陶笛的单价低20元,用2
700元购买A型陶笛与用4
500元购买B型陶笛的数量相同,设A型陶笛的单价为x元,依题意,下面所列方程正确的是(
)
A.=
B.=
C.=
D.=
二、填空题(每小题4分,共24分)
13.分解因式:2a2-4a+2=_______.
14.若a+b=3,ab=2,则(a-b)2=_____.
15.代数式中x的取值范围是________.
16.满足不等式2(x+1)>1-x的最小整数解是________.
17.若方程x2-2x-1=0的两根分别为x1,x2,则x1+x2-x1x2的值为__________.
18.如果实数x,y满足方程组那么x2-y2的值为____________.
三、解答题(共60分)
19.(1)(6分)计算:(2
017)0×-()-1-|-3|+2cos45°.
(2)(6分)计算:(+-1)(-+1).
.
20.(1)(6分)解方程组:
(2).(6分)解方程:=-2.
21.(8分)解不等式组并把解在数轴上表示出来.
17.(8分)已知:x=+1,y=-1,求的值.
22.(8分)先化简,再求值:(+2-x)÷,其中x满足x2-4x+3=0.
23.(12分)某物流公司承接A、B两种货物的运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收运费9
500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨.该物流公司6月份承接的A种货物和B种货物数量与5月份相同,6月份共收取运费13
000元.问:
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物共330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收取多少运输费?
九年级下学期第一次月检测数学试题
一、选择题(每小题3分,共36分)
1.下列四个实数中,绝对值最小的数是(
C
)
A.-5
B.-
C.1
D.4
2.据某省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜旅客约27
700
000人,将27
700
000用科学记数法表示为(
C
)
A.0.277×107
B.0.277×108
C.2.77×107
D.2.77×108
3.如图,数轴上的点A、B分别对应实数a、b,下列结论正确的是(
C
)
A.a>b
B.|a|>|b|
C.-aD.a+b<0
4.下列运算正确的是(
C
)
A.2a3÷a=6
B.(ab2)2=ab4
C.(a+b)(a-b)=a2-b2
D.(a+b)2=a2+b2
5.已知实数x,y满足+(y+1)2=0,则x-y等于(
A
)
A.3
B.-3
C.1
D.-1
6.方程3x+2(1-x)=4的解是(
C
)
A.x=
B.x=
C.x=2
D.x=1
7.二元一次方程组的解是(
A
)
A.
B.
C.
D.
8.一元一次不等式2(x+2)≥6的解在数轴上表示为(
A
)
9.下列方程有两个相等的实数根的是(
C
)
A.x2+x+1=0
B.4x2+x+1=0
C.x2+12x+36=0
D.x2+x-2=0
10.已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是(
B
)
A.5
B.7
C.5或7
D.10
11.若关于x的一元一次不等式组有解,则m的取值范围为(
C
)
A.m>-
B.m≤
C.m>
D.m≤-
12.某校为了丰富学生的校园生活,准备购买一批陶笛,已知A型陶笛比B型陶笛的单价低20元,用2
700元购买A型陶笛与用4
500元购买B型陶笛的数量相同,设A型陶笛的单价为x元,依题意,下面所列方程正确的是(
D
)
A.=
B.=
C.=
D.=
二、填空题(每小题4分,共24分)
13.分解因式:2a2-4a+2=2(a-1)2.
14.若a+b=3,ab=2,则(a-b)2=1.
15.代数式中x的取值范围是x>1.
16.满足不等式2(x+1)>1-x的最小整数解是0.
17.若方程x2-2x-1=0的两根分别为x1,x2,则x1+x2-x1x2的值为3.
18.如果实数x,y满足方程组那么x2-y2的值为-.
三、解答题(共60分)
19.(1)(6分)计算:(2
017)0×-()-1-|-3|+2cos45°.
解:原式=1×2-2-3+2×
=2-2-3+
=-2.
(2)(6分)计算:(+-1)(-+1).
.
解:原式=[+(-1)][-(-1)]
=3-(-1)2
=3-3+2
=2.
20.(1)(6分)解方程组:
解:由①,得y=3-2x.③
把③代入②,得3x-5(3-2x)=11.解得x=2.
将x=2代入③,得y=-1.
∴原方程组的解为
(2).(6分)解方程:=-2.
解:方程两边同乘(x-3),得
1=x-1-2(x-3).
解得x=4.
检验:当x=4时,x-3≠0,
∴x=4是原分式方程的解.
21.(8分)解不等式组并把解在数轴上表示出来.
解:由1+x>-2,得x>-3.
由≤1,得x≤2.
∴不等式组的解集为-3<x≤2.
解集在数轴上表示如下:
22.(8分)已知:x=+1,y=-1,求的值.
解:原式==.
当x=+1,y=-1时,x-y=2,x+y=2.
∴原式==.
23.(8分)先化简,再求值:(+2-x)÷,其中x满足x2-4x+3=0.
解:原式=÷
=·
=-.
解方程x2-4x+3=0,得(x-1)(x-3)=0,
∴x1=1,x2=3.
当x=1时,原分式无意义;
当x=3时,原式=-=-.
24.(12分)某物流公司承接A、B两种货物的运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收运费9
500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨.该物流公司6月份承接的A种货物和B种货物数量与5月份相同,6月份共收取运费13
000元.问:
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物共330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收取多少运输费?
解:(1)设该物流公司5月份运输A、B两种货物各x吨、y吨,依题意,得
解得
答:该物流公司5月份运输A种货物100吨,运输B种货物150吨.
(2)设物流公司7月份运输A种货物a吨,收取w元运输费,则依题意,有
a≤2(330-a).则a≤220.∴a最大为220.
w=70a+40(330-a)=30a+13
200.
∵k=30>0,w随a的增大而增大.
∴当a=220时,w最大=30×220+13
200=19
800(元).
答:该物流公司7月份最多将收取运输费19
800元.
一、选择题(每小题3分,共36分)
1.下列四个实数中,绝对值最小的数是(
)
A.-5
B.-
C.1
D.4
2.据某省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜旅客约27
700
000人,将27
700
000用科学记数法表示为(
)
A.0.277×107
B.0.277×108
C.2.77×107
D.2.77×108
3.如图,数轴上的点A、B分别对应实数a、b,下列结论正确的是(
)
A.a>b
B.|a|>|b|
C.-a
4.下列运算正确的是(
)
A.2a3÷a=6
B.(ab2)2=ab4
C.(a+b)(a-b)=a2-b2
D.(a+b)2=a2+b2
5.已知实数x,y满足+(y+1)2=0,则x-y等于(
A
)
A.3
B.-3
C.1
D.-1
6.方程3x+2(1-x)=4的解是(
)
A.x=
B.x=
C.x=2
D.x=1
7.二元一次方程组的解是(
)
A.
B.
C.
D.
8.一元一次不等式2(x+2)≥6的解在数轴上表示为(
)
9.下列方程有两个相等的实数根的是(
)
A.x2+x+1=0
B.4x2+x+1=0
C.x2+12x+36=0
D.x2+x-2=0
10.已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是(
)
A.5
B.7
C.5或7
D.10
11.若关于x的一元一次不等式组有解,则m的取值范围为(
)
A.m>-
B.m≤
C.m>
D.m≤-
12.某校为了丰富学生的校园生活,准备购买一批陶笛,已知A型陶笛比B型陶笛的单价低20元,用2
700元购买A型陶笛与用4
500元购买B型陶笛的数量相同,设A型陶笛的单价为x元,依题意,下面所列方程正确的是(
)
A.=
B.=
C.=
D.=
二、填空题(每小题4分,共24分)
13.分解因式:2a2-4a+2=_______.
14.若a+b=3,ab=2,则(a-b)2=_____.
15.代数式中x的取值范围是________.
16.满足不等式2(x+1)>1-x的最小整数解是________.
17.若方程x2-2x-1=0的两根分别为x1,x2,则x1+x2-x1x2的值为__________.
18.如果实数x,y满足方程组那么x2-y2的值为____________.
三、解答题(共60分)
19.(1)(6分)计算:(2
017)0×-()-1-|-3|+2cos45°.
(2)(6分)计算:(+-1)(-+1).
.
20.(1)(6分)解方程组:
(2).(6分)解方程:=-2.
21.(8分)解不等式组并把解在数轴上表示出来.
17.(8分)已知:x=+1,y=-1,求的值.
22.(8分)先化简,再求值:(+2-x)÷,其中x满足x2-4x+3=0.
23.(12分)某物流公司承接A、B两种货物的运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收运费9
500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨.该物流公司6月份承接的A种货物和B种货物数量与5月份相同,6月份共收取运费13
000元.问:
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物共330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收取多少运输费?
九年级下学期第一次月检测数学试题
一、选择题(每小题3分,共36分)
1.下列四个实数中,绝对值最小的数是(
C
)
A.-5
B.-
C.1
D.4
2.据某省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜旅客约27
700
000人,将27
700
000用科学记数法表示为(
C
)
A.0.277×107
B.0.277×108
C.2.77×107
D.2.77×108
3.如图,数轴上的点A、B分别对应实数a、b,下列结论正确的是(
C
)
A.a>b
B.|a|>|b|
C.-a
4.下列运算正确的是(
C
)
A.2a3÷a=6
B.(ab2)2=ab4
C.(a+b)(a-b)=a2-b2
D.(a+b)2=a2+b2
5.已知实数x,y满足+(y+1)2=0,则x-y等于(
A
)
A.3
B.-3
C.1
D.-1
6.方程3x+2(1-x)=4的解是(
C
)
A.x=
B.x=
C.x=2
D.x=1
7.二元一次方程组的解是(
A
)
A.
B.
C.
D.
8.一元一次不等式2(x+2)≥6的解在数轴上表示为(
A
)
9.下列方程有两个相等的实数根的是(
C
)
A.x2+x+1=0
B.4x2+x+1=0
C.x2+12x+36=0
D.x2+x-2=0
10.已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是(
B
)
A.5
B.7
C.5或7
D.10
11.若关于x的一元一次不等式组有解,则m的取值范围为(
C
)
A.m>-
B.m≤
C.m>
D.m≤-
12.某校为了丰富学生的校园生活,准备购买一批陶笛,已知A型陶笛比B型陶笛的单价低20元,用2
700元购买A型陶笛与用4
500元购买B型陶笛的数量相同,设A型陶笛的单价为x元,依题意,下面所列方程正确的是(
D
)
A.=
B.=
C.=
D.=
二、填空题(每小题4分,共24分)
13.分解因式:2a2-4a+2=2(a-1)2.
14.若a+b=3,ab=2,则(a-b)2=1.
15.代数式中x的取值范围是x>1.
16.满足不等式2(x+1)>1-x的最小整数解是0.
17.若方程x2-2x-1=0的两根分别为x1,x2,则x1+x2-x1x2的值为3.
18.如果实数x,y满足方程组那么x2-y2的值为-.
三、解答题(共60分)
19.(1)(6分)计算:(2
017)0×-()-1-|-3|+2cos45°.
解:原式=1×2-2-3+2×
=2-2-3+
=-2.
(2)(6分)计算:(+-1)(-+1).
.
解:原式=[+(-1)][-(-1)]
=3-(-1)2
=3-3+2
=2.
20.(1)(6分)解方程组:
解:由①,得y=3-2x.③
把③代入②,得3x-5(3-2x)=11.解得x=2.
将x=2代入③,得y=-1.
∴原方程组的解为
(2).(6分)解方程:=-2.
解:方程两边同乘(x-3),得
1=x-1-2(x-3).
解得x=4.
检验:当x=4时,x-3≠0,
∴x=4是原分式方程的解.
21.(8分)解不等式组并把解在数轴上表示出来.
解:由1+x>-2,得x>-3.
由≤1,得x≤2.
∴不等式组的解集为-3<x≤2.
解集在数轴上表示如下:
22.(8分)已知:x=+1,y=-1,求的值.
解:原式==.
当x=+1,y=-1时,x-y=2,x+y=2.
∴原式==.
23.(8分)先化简,再求值:(+2-x)÷,其中x满足x2-4x+3=0.
解:原式=÷
=·
=-.
解方程x2-4x+3=0,得(x-1)(x-3)=0,
∴x1=1,x2=3.
当x=1时,原分式无意义;
当x=3时,原式=-=-.
24.(12分)某物流公司承接A、B两种货物的运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收运费9
500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨.该物流公司6月份承接的A种货物和B种货物数量与5月份相同,6月份共收取运费13
000元.问:
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物共330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收取多少运输费?
解:(1)设该物流公司5月份运输A、B两种货物各x吨、y吨,依题意,得
解得
答:该物流公司5月份运输A种货物100吨,运输B种货物150吨.
(2)设物流公司7月份运输A种货物a吨,收取w元运输费,则依题意,有
a≤2(330-a).则a≤220.∴a最大为220.
w=70a+40(330-a)=30a+13
200.
∵k=30>0,w随a的增大而增大.
∴当a=220时,w最大=30×220+13
200=19
800(元).
答:该物流公司7月份最多将收取运输费19
800元.
同课章节目录
