18.2.1 矩形(带解析)
图片预览


文档简介
18.2.1 矩形(带解析)
一、选择题
1.已知四边形ABCD中,AC⊥BD,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH是( )【来源:21·世纪·教育·网】
A.菱形 B.矩形 C.正方形 D.梯形
2.下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形 C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
3.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )www.21-cn-jy.com
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
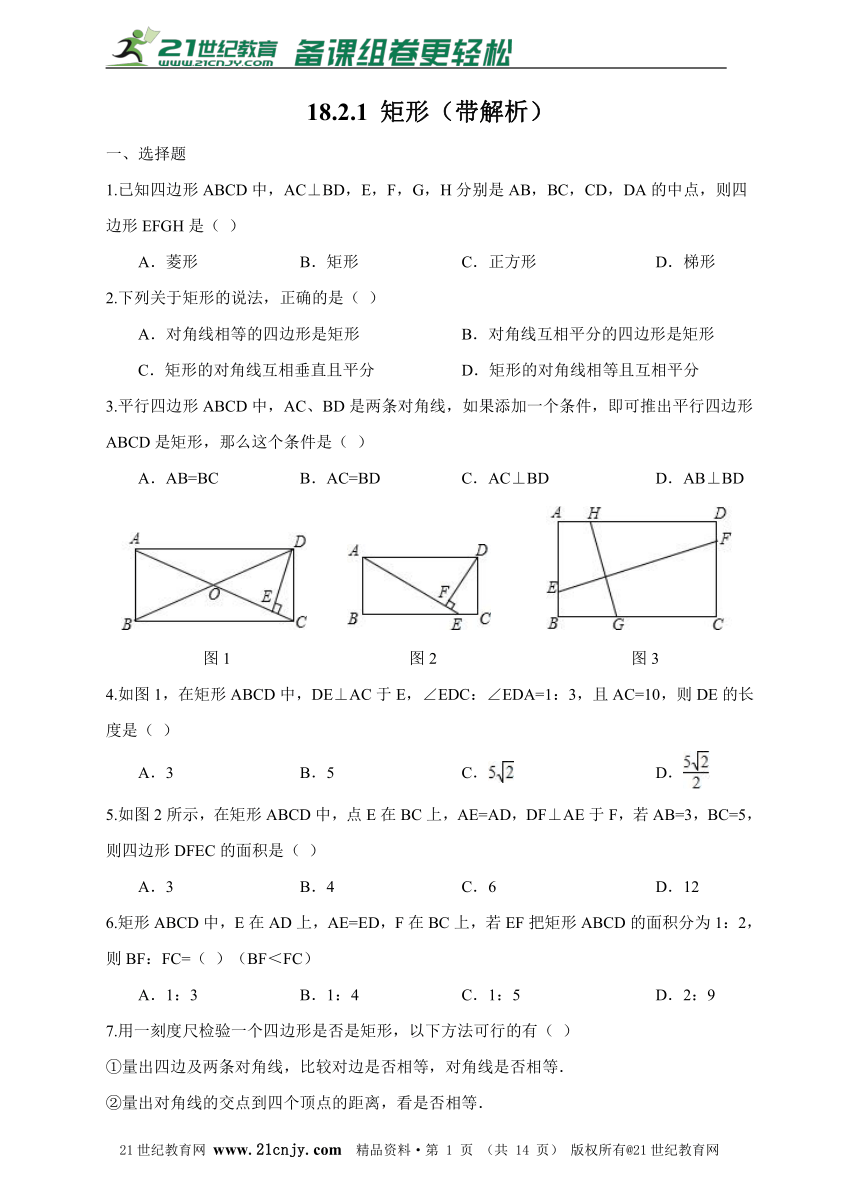
图1 图2 图3
4.如图1,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则DE的长度是( )2·1·c·n·j·y
A.3 B.5 C. D.
5.如图2所示,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,若AB=3,BC=5,则四边形DFEC的面积是( )www-2-1-cnjy-com
A.3 B.4 C.6 D.12
6.矩形ABCD中,E在AD上,AE=ED,F在BC上,若EF把矩形ABCD的面积分为1:2,则BF:FC=( )(BF<FC)2-1-c-n-j-y
A.1:3 B.1:4 C.1:5 D.2:9
7.用一刻度尺检验一个四边形是否是矩形,以下方法可行的有( ) ①量出四边及两条对角线,比较对边是否相等,对角线是否相等. ②量出对角线的交点到四个顶点的距离,看是否相等. ③量出一组邻的长a、b以及和这两边组成三角形的那条对角线的长c,计算是否有a2+b2=c2. ④量出两条对角线长,看是否相等.【来源:21cnj*y.co*m】
A.一种 B.二种 C.三种 D.四种
二、填空题
8.如图3,E,G,F,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB=2,BC=3,则EF:GH=??? .21世纪教育网版权所有
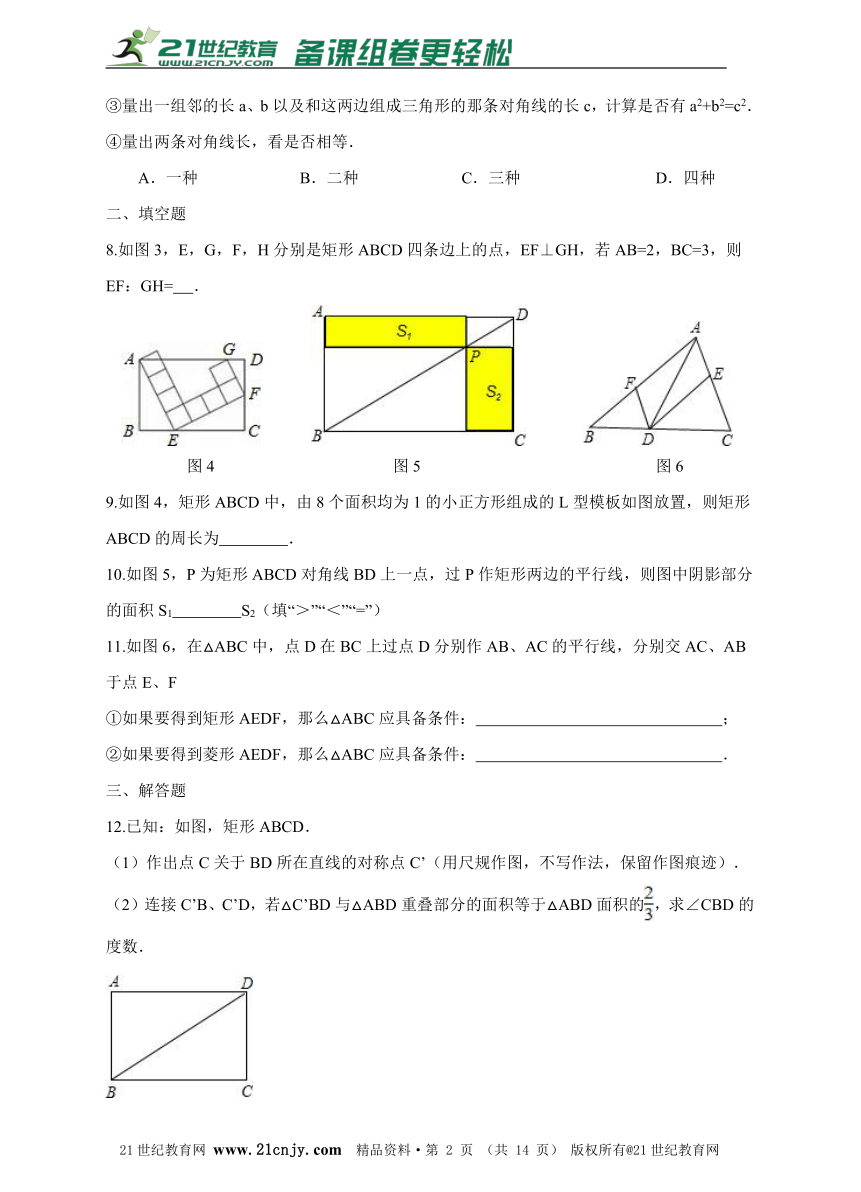
图4 图5 图6
9.如图4,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为??? .21教育网
10.如图5,P为矩形ABCD对角线BD上一点,过P作矩形两边的平行线,则图中阴影部分的面积S1??? S2(填“>”“<”“=”)21cnjy.com
11.如图6,在△ABC中,点D在BC上过点D分别作AB、AC的平行线,分别交AC、AB于点E、F ①如果要得到矩形AEDF,那么△ABC应具备条件:??? ; ②如果要得到菱形AEDF,那么△ABC应具备条件:??? .
三、解答题
12.已知:如图,矩形ABCD. (1)作出点C关于BD所在直线的对称点C’(用尺规作图,不写作法,保留作图痕迹). (2)连接C’B、C’D,若△C’BD与△ABD重叠部分的面积等于△ABD面积的,求∠CBD的度数.21*cnjy*com
13.如图所示,以△ABC的三边为边,分别作三个等边三角形. (1)求证四边形ADEF是平行四边形; (2)△ABC满足什么条件时,四边形ADEF是菱形是矩形? (3)这样的平行四边形ADEF是否总是存在?21·世纪*教育网
14.已知:平行四边形ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD,A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图). (1)求证:四边形ABCD是矩形; (2)在四边形ABCD中,求的值.【出处:21教育名师】
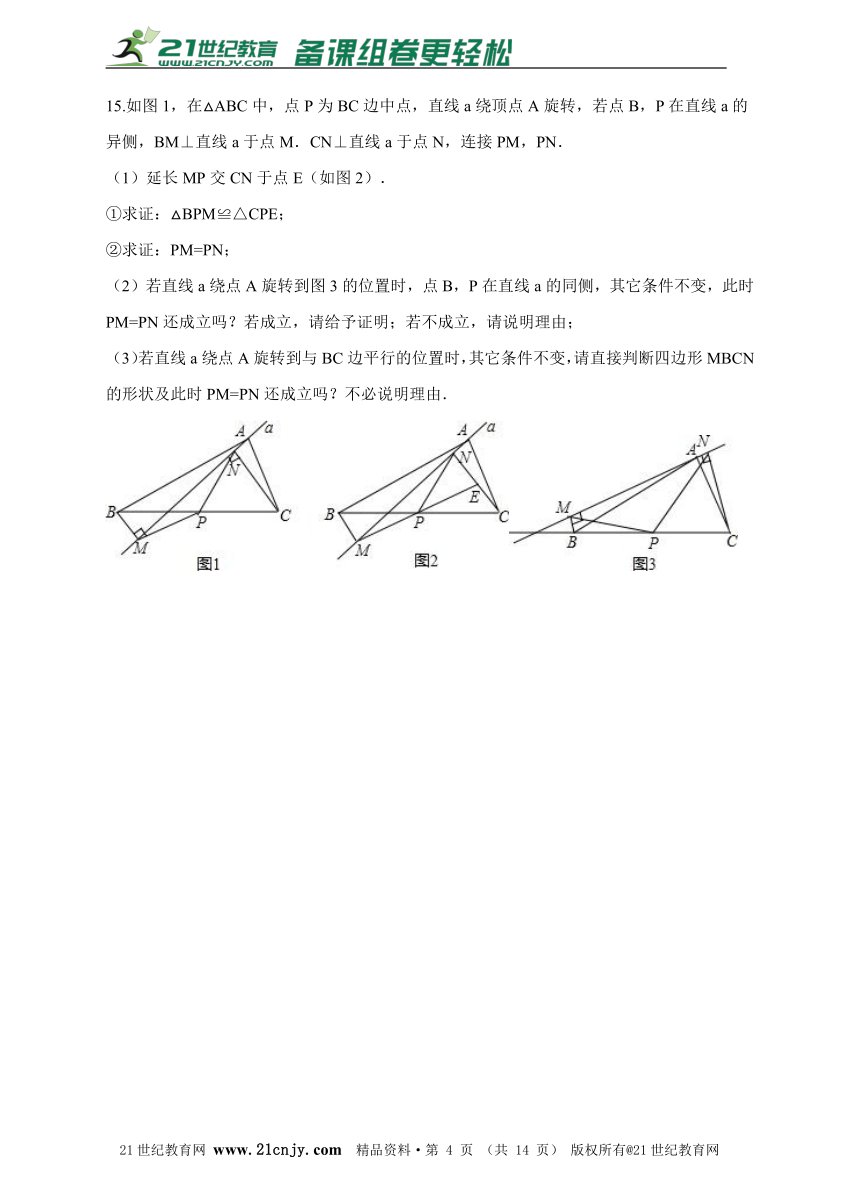
15.如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN. (1)延长MP交CN于点E(如图2). ①求证:△BPM≌△CPE; ②求证:PM=PN; (2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由; (3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.【版权所有:21教育】
参考答案及解析
1.B 【解析】如图 依题意四边形ABCD,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点, 根据矩形的判定(矩形的对角线相等且相互平分)可得四边形EFGH是矩形. 2.D 【解析】A、因为对角线相等的平行四边形是矩形,所以本选项错误;
∴OC=OD, ∴∠ODC=∠OCD, ∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°, ∴∠EDC=22.5°,∠EDA=67.5°, ∵DE⊥AC, ∴∠DEC=90°, ∴∠DCE=90°-∠EDC=67.5°, ∴∠ODC=∠OCD=67.5°, ∴∠ODC+∠OCD+∠DOC=180°, ∴∠COD=45°, ∴OE=DE, ∵OE2+DE2=OD2, ∴(2DE)2=OD2=25, ∴DE=, 5.A 【解析】如图连接DE, ∵AE=AD,∴∠ADE=∠AED, ∵DF⊥AE,∴∠EDF+∠AED=90°, ∵∠ADE+∠CDE=90°, ∴∠FDE=∠CDE,又DE=DE,∠DFE=∠C=90°,
则BF:FC=:=1:5. 7.B 【解析】①先测量两组对边是否相等,然后测量两条对角线是否相等;理由:两组对边分别相等的四边形是平行四边形,可以判定是否是矩形; ②根据对角线相等且互相平分四边形是矩形,可知量出对角线的交点到四个顶点的距离,看是否相等,可判断是否是矩形. ③量出一组邻的长a、b以及和这两边组成三角形的那条对角线的长c,计算是否有a2+b2=c2.可以判断是否是直角,但不能判断是否是矩形; ④量出两条对角线长,看是否相等不能判定是矩形,必须两条对角线长相等气且互相平分才是矩形; 8.3:2 【解析】21·cn·jy·com
过点H,F作HM⊥BC,FN⊥BC, 由EF⊥GH,∠GHM+∠HON=∠EFN+∠FOG=90°, 又∵∠HON=∠FOG(对顶角相等),
∴GD=,FD=, ∵∠BAE+∠AEB=90°=∠FEC+∠AEB, ∴∠BAE=∠FEC, ∵∠B=∠C=90°,AE=EF, ∴△ABE≌△ECF(AAS), ∴AB=CE,CF=BE,
在△ABD和△CDB中, ∴△ABD≌△CDB, ∴S△ABD=S△CDB, 同理S△DEP=S△PHD,S△PGB=S△PBF, ∴S1=S2. 11.∠BAC=90°,AD平分∠BAC 【解析】∵DE∥AB,DF∥AC,AF、AE分别在AB、AC上 ∴DE∥AF,DF∥AE ∴四边形AEDF是平行四边形 ①∵∠BAC=90° ∴四边形AEDF是矩形; ②∵AD是△ABC的角平分线, ∴∠DAE=∠DAF ∴∠ADE=∠DAE ∴∠DBC=∠EDB, ∴∠EDB=∠EBD ∴BE=ED. ∴在直角△ABE中,BE=2AE. ∴∠ABE=30°. ∴∠CBD=∠CBC'=30°. 13.(1)见解析 (2)当∠BAC=150°时,四边形ADEF是矩形 (3)即D,A,F三点在同一直线上时,不存在这样的平行四边形ADEF
【解析】(1)证明:∵△ABD,△BCE,△ACF都是等边三角形, ∴AB=BD=AD,∠ABD=∠EBC=∠BCE=∠ACF=60°,
又AB=AC, ∴AD=AF. 又∵四边形ADEF为平行四边形, ∴平行四边形ADEF是菱形. 当∠BAC=150°时,四边形ADEF是矩形. 理由如下: ∵∠BAD=∠CAF=60°,∠BAC=150°,∠BAD+∠CAF+∠BAC+∠DAF=360°, ∠DAF=90度. 又∵四边形ADEF是平行四边形, ∴四边形平行四边形ADEF是矩形. (3)解:当∠BAC=60°时,不存在这样的平行四边形ADEF.理由如下: ∵当∠BAC=60°时, 21教育名师原创作品
∴DE=BE, ∴EO⊥BD, ∴∠DOE=90°, 即∠DAE=90°, 又四边形ABCD是平行四边形, ∴四边形ABCD是矩形. (2)解:∵四边形DEBF是菱形, ∴∠FDB=∠EDB, 又由题意知∠EDB=∠EDA, 由(1)知四边形ABCD是矩形, ∴∠ADF=90°,即∠FDB+∠EDB+∠ADE=90°, 则∠ADB=60°, ∴在Rt△ADB中,有AD:AB=1:, 又BC=AD,
又∵P为BC边中点, ∴BP=CP, 又∵∠BPM=∠CPE, ∴△BPM≌△CPE,
②∵△BPM≌△CPE, ∴PM=PE∴PM=ME, ∴在Rt△MNE中,PN=ME, ∴PM=PN. (2)21*cnjy*com
成立,如图3. 证明:延长MP与NC的延长线相交于点E, ∵BM⊥直线a于点M,CN⊥直线a于点N,
(3)
解:如图4, 四边形M′BCN′是矩形, 根据矩形的性质和P为BC边中点,得到△M′BP≌△N′CP, 得PM′=PN′成立.即“四边形MBCN是矩形,则PM=PN成立”.
一、选择题
1.已知四边形ABCD中,AC⊥BD,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH是( )【来源:21·世纪·教育·网】
A.菱形 B.矩形 C.正方形 D.梯形
2.下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形 C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
3.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )www.21-cn-jy.com
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
图1 图2 图3
4.如图1,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则DE的长度是( )2·1·c·n·j·y
A.3 B.5 C. D.
5.如图2所示,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,若AB=3,BC=5,则四边形DFEC的面积是( )www-2-1-cnjy-com
A.3 B.4 C.6 D.12
6.矩形ABCD中,E在AD上,AE=ED,F在BC上,若EF把矩形ABCD的面积分为1:2,则BF:FC=( )(BF<FC)2-1-c-n-j-y
A.1:3 B.1:4 C.1:5 D.2:9
7.用一刻度尺检验一个四边形是否是矩形,以下方法可行的有( ) ①量出四边及两条对角线,比较对边是否相等,对角线是否相等. ②量出对角线的交点到四个顶点的距离,看是否相等. ③量出一组邻的长a、b以及和这两边组成三角形的那条对角线的长c,计算是否有a2+b2=c2. ④量出两条对角线长,看是否相等.【来源:21cnj*y.co*m】
A.一种 B.二种 C.三种 D.四种
二、填空题
8.如图3,E,G,F,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB=2,BC=3,则EF:GH=??? .21世纪教育网版权所有
图4 图5 图6
9.如图4,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为??? .21教育网
10.如图5,P为矩形ABCD对角线BD上一点,过P作矩形两边的平行线,则图中阴影部分的面积S1??? S2(填“>”“<”“=”)21cnjy.com
11.如图6,在△ABC中,点D在BC上过点D分别作AB、AC的平行线,分别交AC、AB于点E、F ①如果要得到矩形AEDF,那么△ABC应具备条件:??? ; ②如果要得到菱形AEDF,那么△ABC应具备条件:??? .
三、解答题
12.已知:如图,矩形ABCD. (1)作出点C关于BD所在直线的对称点C’(用尺规作图,不写作法,保留作图痕迹). (2)连接C’B、C’D,若△C’BD与△ABD重叠部分的面积等于△ABD面积的,求∠CBD的度数.21*cnjy*com
13.如图所示,以△ABC的三边为边,分别作三个等边三角形. (1)求证四边形ADEF是平行四边形; (2)△ABC满足什么条件时,四边形ADEF是菱形是矩形? (3)这样的平行四边形ADEF是否总是存在?21·世纪*教育网
14.已知:平行四边形ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD,A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图). (1)求证:四边形ABCD是矩形; (2)在四边形ABCD中,求的值.【出处:21教育名师】
15.如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN. (1)延长MP交CN于点E(如图2). ①求证:△BPM≌△CPE; ②求证:PM=PN; (2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由; (3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.【版权所有:21教育】
参考答案及解析
1.B 【解析】如图 依题意四边形ABCD,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点, 根据矩形的判定(矩形的对角线相等且相互平分)可得四边形EFGH是矩形. 2.D 【解析】A、因为对角线相等的平行四边形是矩形,所以本选项错误;
∴OC=OD, ∴∠ODC=∠OCD, ∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°, ∴∠EDC=22.5°,∠EDA=67.5°, ∵DE⊥AC, ∴∠DEC=90°, ∴∠DCE=90°-∠EDC=67.5°, ∴∠ODC=∠OCD=67.5°, ∴∠ODC+∠OCD+∠DOC=180°, ∴∠COD=45°, ∴OE=DE, ∵OE2+DE2=OD2, ∴(2DE)2=OD2=25, ∴DE=, 5.A 【解析】如图连接DE, ∵AE=AD,∴∠ADE=∠AED, ∵DF⊥AE,∴∠EDF+∠AED=90°, ∵∠ADE+∠CDE=90°, ∴∠FDE=∠CDE,又DE=DE,∠DFE=∠C=90°,
则BF:FC=:=1:5. 7.B 【解析】①先测量两组对边是否相等,然后测量两条对角线是否相等;理由:两组对边分别相等的四边形是平行四边形,可以判定是否是矩形; ②根据对角线相等且互相平分四边形是矩形,可知量出对角线的交点到四个顶点的距离,看是否相等,可判断是否是矩形. ③量出一组邻的长a、b以及和这两边组成三角形的那条对角线的长c,计算是否有a2+b2=c2.可以判断是否是直角,但不能判断是否是矩形; ④量出两条对角线长,看是否相等不能判定是矩形,必须两条对角线长相等气且互相平分才是矩形; 8.3:2 【解析】21·cn·jy·com
过点H,F作HM⊥BC,FN⊥BC, 由EF⊥GH,∠GHM+∠HON=∠EFN+∠FOG=90°, 又∵∠HON=∠FOG(对顶角相等),
∴GD=,FD=, ∵∠BAE+∠AEB=90°=∠FEC+∠AEB, ∴∠BAE=∠FEC, ∵∠B=∠C=90°,AE=EF, ∴△ABE≌△ECF(AAS), ∴AB=CE,CF=BE,
在△ABD和△CDB中, ∴△ABD≌△CDB, ∴S△ABD=S△CDB, 同理S△DEP=S△PHD,S△PGB=S△PBF, ∴S1=S2. 11.∠BAC=90°,AD平分∠BAC 【解析】∵DE∥AB,DF∥AC,AF、AE分别在AB、AC上 ∴DE∥AF,DF∥AE ∴四边形AEDF是平行四边形 ①∵∠BAC=90° ∴四边形AEDF是矩形; ②∵AD是△ABC的角平分线, ∴∠DAE=∠DAF ∴∠ADE=∠DAE ∴∠DBC=∠EDB, ∴∠EDB=∠EBD ∴BE=ED. ∴在直角△ABE中,BE=2AE. ∴∠ABE=30°. ∴∠CBD=∠CBC'=30°. 13.(1)见解析 (2)当∠BAC=150°时,四边形ADEF是矩形 (3)即D,A,F三点在同一直线上时,不存在这样的平行四边形ADEF
【解析】(1)证明:∵△ABD,△BCE,△ACF都是等边三角形, ∴AB=BD=AD,∠ABD=∠EBC=∠BCE=∠ACF=60°,
又AB=AC, ∴AD=AF. 又∵四边形ADEF为平行四边形, ∴平行四边形ADEF是菱形. 当∠BAC=150°时,四边形ADEF是矩形. 理由如下: ∵∠BAD=∠CAF=60°,∠BAC=150°,∠BAD+∠CAF+∠BAC+∠DAF=360°, ∠DAF=90度. 又∵四边形ADEF是平行四边形, ∴四边形平行四边形ADEF是矩形. (3)解:当∠BAC=60°时,不存在这样的平行四边形ADEF.理由如下: ∵当∠BAC=60°时, 21教育名师原创作品
∴DE=BE, ∴EO⊥BD, ∴∠DOE=90°, 即∠DAE=90°, 又四边形ABCD是平行四边形, ∴四边形ABCD是矩形. (2)解:∵四边形DEBF是菱形, ∴∠FDB=∠EDB, 又由题意知∠EDB=∠EDA, 由(1)知四边形ABCD是矩形, ∴∠ADF=90°,即∠FDB+∠EDB+∠ADE=90°, 则∠ADB=60°, ∴在Rt△ADB中,有AD:AB=1:, 又BC=AD,
又∵P为BC边中点, ∴BP=CP, 又∵∠BPM=∠CPE, ∴△BPM≌△CPE,
②∵△BPM≌△CPE, ∴PM=PE∴PM=ME, ∴在Rt△MNE中,PN=ME, ∴PM=PN. (2)21*cnjy*com
成立,如图3. 证明:延长MP与NC的延长线相交于点E, ∵BM⊥直线a于点M,CN⊥直线a于点N,
(3)
解:如图4, 四边形M′BCN′是矩形, 根据矩形的性质和P为BC边中点,得到△M′BP≌△N′CP, 得PM′=PN′成立.即“四边形MBCN是矩形,则PM=PN成立”.
