陕西省黄陵中学2016-2017学年高二下学期第一次月检测数学(文)试题(重点班) Word版含答案
文档属性
| 名称 | 陕西省黄陵中学2016-2017学年高二下学期第一次月检测数学(文)试题(重点班) Word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 137.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-31 00:00:00 | ||
图片预览




文档简介
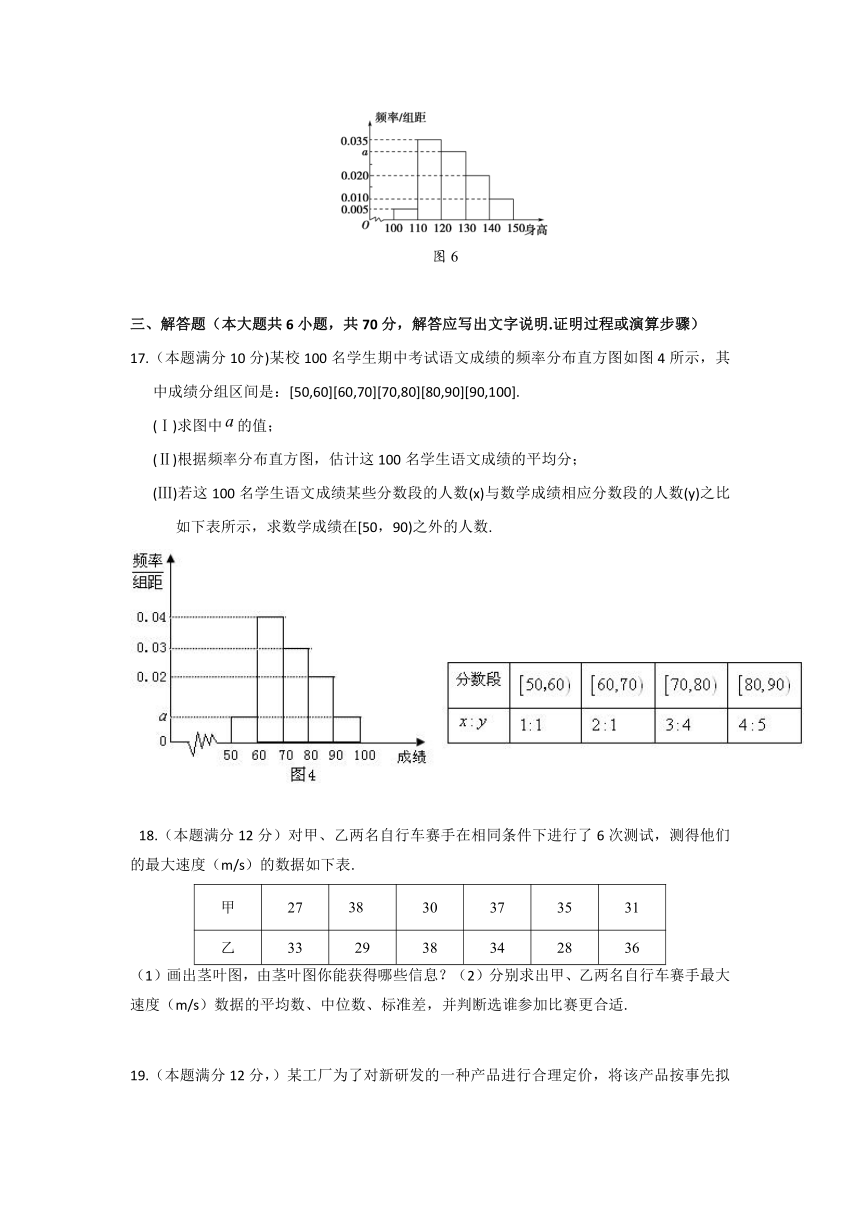
高二文科重点月考
数学试题
(考试时间120分钟,满分150分)姓名_______评价______
一、选择题(每小题5分,共60分.
以下给出的四个备选答案中,只有一个正确)
1.某学校为了调查高一年级的200名学生完成课后作业所需时间,采取了两种抽样调查的方式:第一种由学生会的同学随机抽取20名同学进行抽查;第二种由教务处对该年级的学生进行编号,从001到200,抽取学号最后一位为2的同学进行调查.则这两种抽样的方法依次是( )
A.分层抽样,简单随机抽样
B.简单随机抽样,分层抽样
C.分层抽样,系统抽样
D.简单随机抽样,系统抽样
2.小波一星期的总开支分布如图1①所示,一星期的食品开支如图1②所示,则小波一星期的鸡蛋开支占总开支的百分比为( )
图1
A.1%
B.2%
C.3%
D.5%
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,则由此求出的平均数与实际平均数的差是( )
A.3.5
B.-3
C.3
D.-0.5
4.根据统计,一名工作组装第x件某产品所用的时间(单位:分钟)为
(A,C为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么C和
A的值分别是(
)
A.75,25
B.75,16
C.60,25
D.60,16
5.某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是(
)
A.简单随机抽样法
B.抽签法
C.随机数表法
D.分层抽样法
6.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则改样本的中位数、众数、极差分别是( )
A.46,45,56
B.46,45,53
C.47,45,56
D.45,47,53
7.在某项体育比赛中一位同学被评委所打出的分数如下:
90
89
90
95
93
94
93
去掉一个最高分和一个最低分后,所剩数据的平均分值为和方差分别为(
)
A.
92,2
B.
92
,2.8
C.
93,2
D.93,2.8
8、回归方程=1.5x-15,则下列结论正确的是
A.=1.5-15
B.15是回归系数a
C.1.5是回归系数a
D.x=10时,y=0
9、已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是
A.[5.5,7.5)
B.[7.5,9.5)
C.[9.5,11.5)
D.[11.5,13.5)
10、某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取一个容量为45的样本,那么高一、高二、高三各年级抽取人数分别为
A.15,5,25
B.15,15,15
C.10,5,30
D.15,10,20
11.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),表示变量Y与X之间的线性相关系数,表示变量V与U之间的线性相关系数,则(
)
A.
B.
C.
D.
12.某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程中的为9.4,据此模型预报广告费用为6万元时销售额为
A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡中对应题号后的横线上)
13.从50个产品中抽取10个进行检查,则总体个数为_______,样本容量为______.
14.由正整数组成的一组数据、、、,其平均数和中位数都是2,且标准差等于1,则这组数据为_________.(从小到大排列)
15.图2是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为_________.
(注:方差,其中为x1,x2,,xn的平均数)
16.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图6).由图中数据可知a=________.若要从身高在[120,130),[130,140),[140,150]三组的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]的学生中选取的人数应为________.
图6
三、解答题(本大题共6小题,共70分,解答应写出文字说明.证明过程或演算步骤)
17.(本题满分10分)某校100名学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是:[50,60][60,70][70,80][80,90][90,100].
(Ⅰ)求图中的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
18.(本题满分12分)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
甲
27
38
30
37
35
31
乙
33
29
38
34
28
36
(1)画出茎叶图,由茎叶图你能获得哪些信息?(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
19.(本题满分12分,)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元)
8
8.2
8.4
8.6
8.8
9
销量y(件)
90
84
83
80
75
68
(Ⅰ)求回归直线方程,其中
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入—成本)
20.(本题满分12分,)一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,
8.6,
9.2,
9.6,
8.7,
9.3,
9.0,
8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
21.(本题满分12分,)有一种鱼的身体吸收水银,水银的含量超过1.00
ppm(即百万分之一)时就会对人体产生危害.在30条鱼的样本中发现的水银含量是:
0.07
0.24
0.95
0.98
1.02
0.98
1.37
1.40
0.39
1.02
1.44
1.58
0.54
1.08
0.61
0.72
1.20
1.14
1.62
1.68
1.85
1.20
0.81
0.82
0.84
1.29
1.26
2.10
0.91
1.31
(1)用前两位数作为茎,做出样本数据的茎叶图;
(2)描述一下水银含量的分布特点;
(3)从实际情况看,许多鱼的水银含量超标在于有些鱼在出售之前没有被检查过.那么,这种鱼的水银含量的平均水平都比1.00
ppm大吗
(4)求出上述样本数据的均值和标准差;
(5)有多少条鱼的水银含量在均值减加两倍标准差的范围内?
22.(本题满分12分)一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,
8.6,
9.2,
9.6,
8.7,
9.3,
9.0,
8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
参考答案
一、选择题答题卡:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
B
D
D
C
B
A
D
D
C
B
二、填空题
13.50,10
14..
15.
6.8
.
16. 0.030 3
三、解答题
17.
解:
(Ⅰ)
(Ⅱ)平均分为
(Ⅲ)数学成绩在内的人数为人,数学成绩在外的人数为人.
答:(Ⅰ)
;(Ⅱ)这100名学生语文成绩的平均分为73;(Ⅲ)数学成绩在外的人数为10人.
18.解:解:(1)画茎叶图,中间数为数据的十位数
从这个茎叶图上可以看出,甲、乙的得分情况都是分布均匀的,只是乙更好一些;乙的中位数是35,甲的中位数是33.因此乙发挥比较稳定,总体得分情况比甲好.
(2)利用科学计算器:=33,=33;=3.96,=3.56;甲的中位数是33,乙的中位数是33.5.
综合比较选乙参加比赛较为合适.
19.
解:(Ⅰ)由于,
所以,从而回归直线方程为.
(Ⅱ)设工厂获得的利润为L元,依题意得
当且仅当时,L取得最大值.
故当单价定为8.25元时,工厂可获得最大利润.
20.
解:
(Ⅰ)设该厂本月生产轿车为n辆,由题意得,,
所以n=2000.
z=2000-100-300-150-450-600=400
(Ⅱ)
设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1,
B1),
(S1,
B2)
,
(S1,
B3)
(S2
,B1),
(S2
,B2),
(S2
,B3),(
(S1,
S2),(B1
,B2),
(B2
,B3)
,(B1
,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件:
(S1,
B1),
(S1,
B2)
,
(S1,
B3)
(S2
,B1),
(S2
,B2),
(S2
,B3),(
(S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为.
(Ⅲ)样本的平均数为,
那么与样本平均数之差的绝对值不超过0.5的数为9.4,
8.6,
9.2,
8.7,
9.3,
9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为.
21.
解析:
(1)茎叶图为:
茎
叶
0.0
7
0.2
4
0.3
9
0.5
4
0.6
1
0.7
2
0.8
124
0.9
1588
1.0
228
1.1
4
1.2
0069
1.3
17
1.4
04
1.5
8
1.6
28
1.8
5
2.1
0
(2)汞含量分布偏向于大于1.00
ppm的方向,即多数鱼的汞含量分布在大于1.00
ppm的区域.
(3)不一定.
因为我们不知道各批鱼的汞含量分布是否都和这批鱼相同.即使各批鱼的汞含量分布相同,上面的数据只能为这个分布作出估计,不能保证平均汞含量大于1.00
ppm.
(4)样本平均数≈1.08,样本标准差s≈0.45.
(5)有28条鱼的汞含量在平均数与两倍标准差的和(差)的范围内.
22.
解:
(Ⅰ)设该厂本月生产轿车为n辆,由题意得,,
所以n=2000.
z=2000-100-300-150-450-600=400
(Ⅱ)
设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1,
B1),
(S1,
B2)
,
(S1,
B3)
(S2
,B1),
(S2
,B2),
(S2
,B3),(
(S1,
S2),(B1
,B2),
(B2
,B3)
,(B1
,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件:
(S1,
B1),
(S1,
B2)
,
(S1,
B3)
(S2
,B1),
(S2
,B2),
(S2,B3),(
(S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为.
(Ⅲ)样本的平均数为,
那么与样本平均数之差的绝对值不超过0.5的数为9.4,
8.6,
9.2,
8.7,
9.3,
9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为.
1
25
2
0233
3
124489
4
5577889
5
0011479
6
178
数学试题
(考试时间120分钟,满分150分)姓名_______评价______
一、选择题(每小题5分,共60分.
以下给出的四个备选答案中,只有一个正确)
1.某学校为了调查高一年级的200名学生完成课后作业所需时间,采取了两种抽样调查的方式:第一种由学生会的同学随机抽取20名同学进行抽查;第二种由教务处对该年级的学生进行编号,从001到200,抽取学号最后一位为2的同学进行调查.则这两种抽样的方法依次是( )
A.分层抽样,简单随机抽样
B.简单随机抽样,分层抽样
C.分层抽样,系统抽样
D.简单随机抽样,系统抽样
2.小波一星期的总开支分布如图1①所示,一星期的食品开支如图1②所示,则小波一星期的鸡蛋开支占总开支的百分比为( )
图1
A.1%
B.2%
C.3%
D.5%
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,则由此求出的平均数与实际平均数的差是( )
A.3.5
B.-3
C.3
D.-0.5
4.根据统计,一名工作组装第x件某产品所用的时间(单位:分钟)为
(A,C为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么C和
A的值分别是(
)
A.75,25
B.75,16
C.60,25
D.60,16
5.某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是(
)
A.简单随机抽样法
B.抽签法
C.随机数表法
D.分层抽样法
6.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则改样本的中位数、众数、极差分别是( )
A.46,45,56
B.46,45,53
C.47,45,56
D.45,47,53
7.在某项体育比赛中一位同学被评委所打出的分数如下:
90
89
90
95
93
94
93
去掉一个最高分和一个最低分后,所剩数据的平均分值为和方差分别为(
)
A.
92,2
B.
92
,2.8
C.
93,2
D.93,2.8
8、回归方程=1.5x-15,则下列结论正确的是
A.=1.5-15
B.15是回归系数a
C.1.5是回归系数a
D.x=10时,y=0
9、已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是
A.[5.5,7.5)
B.[7.5,9.5)
C.[9.5,11.5)
D.[11.5,13.5)
10、某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取一个容量为45的样本,那么高一、高二、高三各年级抽取人数分别为
A.15,5,25
B.15,15,15
C.10,5,30
D.15,10,20
11.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),表示变量Y与X之间的线性相关系数,表示变量V与U之间的线性相关系数,则(
)
A.
B.
C.
D.
12.某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程中的为9.4,据此模型预报广告费用为6万元时销售额为
A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡中对应题号后的横线上)
13.从50个产品中抽取10个进行检查,则总体个数为_______,样本容量为______.
14.由正整数组成的一组数据、、、,其平均数和中位数都是2,且标准差等于1,则这组数据为_________.(从小到大排列)
15.图2是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为_________.
(注:方差,其中为x1,x2,,xn的平均数)
16.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图6).由图中数据可知a=________.若要从身高在[120,130),[130,140),[140,150]三组的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]的学生中选取的人数应为________.
图6
三、解答题(本大题共6小题,共70分,解答应写出文字说明.证明过程或演算步骤)
17.(本题满分10分)某校100名学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是:[50,60][60,70][70,80][80,90][90,100].
(Ⅰ)求图中的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
18.(本题满分12分)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
甲
27
38
30
37
35
31
乙
33
29
38
34
28
36
(1)画出茎叶图,由茎叶图你能获得哪些信息?(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.
19.(本题满分12分,)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元)
8
8.2
8.4
8.6
8.8
9
销量y(件)
90
84
83
80
75
68
(Ⅰ)求回归直线方程,其中
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入—成本)
20.(本题满分12分,)一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,
8.6,
9.2,
9.6,
8.7,
9.3,
9.0,
8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
21.(本题满分12分,)有一种鱼的身体吸收水银,水银的含量超过1.00
ppm(即百万分之一)时就会对人体产生危害.在30条鱼的样本中发现的水银含量是:
0.07
0.24
0.95
0.98
1.02
0.98
1.37
1.40
0.39
1.02
1.44
1.58
0.54
1.08
0.61
0.72
1.20
1.14
1.62
1.68
1.85
1.20
0.81
0.82
0.84
1.29
1.26
2.10
0.91
1.31
(1)用前两位数作为茎,做出样本数据的茎叶图;
(2)描述一下水银含量的分布特点;
(3)从实际情况看,许多鱼的水银含量超标在于有些鱼在出售之前没有被检查过.那么,这种鱼的水银含量的平均水平都比1.00
ppm大吗
(4)求出上述样本数据的均值和标准差;
(5)有多少条鱼的水银含量在均值减加两倍标准差的范围内?
22.(本题满分12分)一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,
8.6,
9.2,
9.6,
8.7,
9.3,
9.0,
8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
参考答案
一、选择题答题卡:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
B
D
D
C
B
A
D
D
C
B
二、填空题
13.50,10
14..
15.
6.8
.
16. 0.030 3
三、解答题
17.
解:
(Ⅰ)
(Ⅱ)平均分为
(Ⅲ)数学成绩在内的人数为人,数学成绩在外的人数为人.
答:(Ⅰ)
;(Ⅱ)这100名学生语文成绩的平均分为73;(Ⅲ)数学成绩在外的人数为10人.
18.解:解:(1)画茎叶图,中间数为数据的十位数
从这个茎叶图上可以看出,甲、乙的得分情况都是分布均匀的,只是乙更好一些;乙的中位数是35,甲的中位数是33.因此乙发挥比较稳定,总体得分情况比甲好.
(2)利用科学计算器:=33,=33;=3.96,=3.56;甲的中位数是33,乙的中位数是33.5.
综合比较选乙参加比赛较为合适.
19.
解:(Ⅰ)由于,
所以,从而回归直线方程为.
(Ⅱ)设工厂获得的利润为L元,依题意得
当且仅当时,L取得最大值.
故当单价定为8.25元时,工厂可获得最大利润.
20.
解:
(Ⅰ)设该厂本月生产轿车为n辆,由题意得,,
所以n=2000.
z=2000-100-300-150-450-600=400
(Ⅱ)
设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1,
B1),
(S1,
B2)
,
(S1,
B3)
(S2
,B1),
(S2
,B2),
(S2
,B3),(
(S1,
S2),(B1
,B2),
(B2
,B3)
,(B1
,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件:
(S1,
B1),
(S1,
B2)
,
(S1,
B3)
(S2
,B1),
(S2
,B2),
(S2
,B3),(
(S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为.
(Ⅲ)样本的平均数为,
那么与样本平均数之差的绝对值不超过0.5的数为9.4,
8.6,
9.2,
8.7,
9.3,
9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为.
21.
解析:
(1)茎叶图为:
茎
叶
0.0
7
0.2
4
0.3
9
0.5
4
0.6
1
0.7
2
0.8
124
0.9
1588
1.0
228
1.1
4
1.2
0069
1.3
17
1.4
04
1.5
8
1.6
28
1.8
5
2.1
0
(2)汞含量分布偏向于大于1.00
ppm的方向,即多数鱼的汞含量分布在大于1.00
ppm的区域.
(3)不一定.
因为我们不知道各批鱼的汞含量分布是否都和这批鱼相同.即使各批鱼的汞含量分布相同,上面的数据只能为这个分布作出估计,不能保证平均汞含量大于1.00
ppm.
(4)样本平均数≈1.08,样本标准差s≈0.45.
(5)有28条鱼的汞含量在平均数与两倍标准差的和(差)的范围内.
22.
解:
(Ⅰ)设该厂本月生产轿车为n辆,由题意得,,
所以n=2000.
z=2000-100-300-150-450-600=400
(Ⅱ)
设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1,
B1),
(S1,
B2)
,
(S1,
B3)
(S2
,B1),
(S2
,B2),
(S2
,B3),(
(S1,
S2),(B1
,B2),
(B2
,B3)
,(B1
,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件:
(S1,
B1),
(S1,
B2)
,
(S1,
B3)
(S2
,B1),
(S2
,B2),
(S2,B3),(
(S1,
S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为.
(Ⅲ)样本的平均数为,
那么与样本平均数之差的绝对值不超过0.5的数为9.4,
8.6,
9.2,
8.7,
9.3,
9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为.
1
25
2
0233
3
124489
4
5577889
5
0011479
6
178
同课章节目录
