数学六年级下西师大版5数的认识(2)课件(27张)
文档属性
| 名称 | 数学六年级下西师大版5数的认识(2)课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-01 16:26:50 | ||
图片预览






文档简介
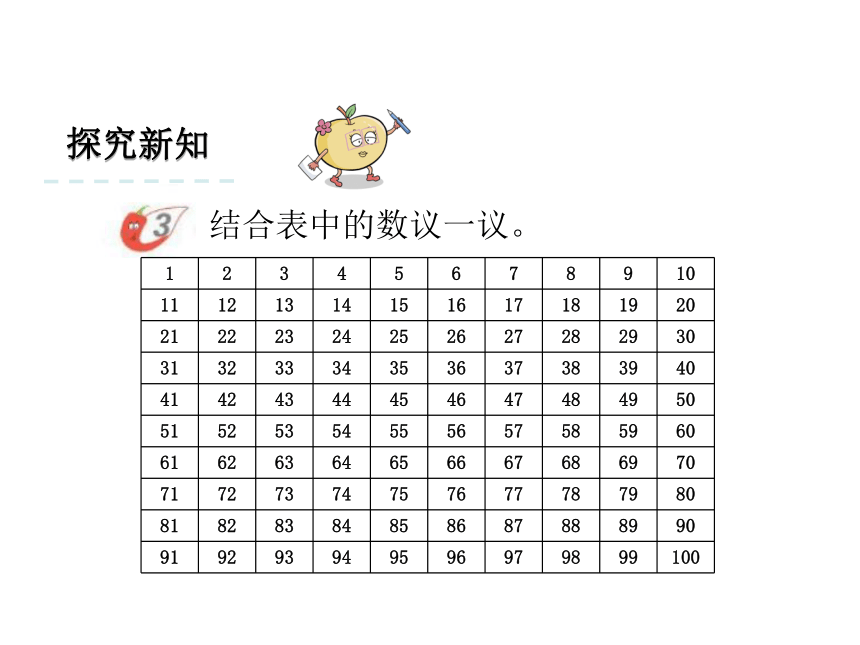
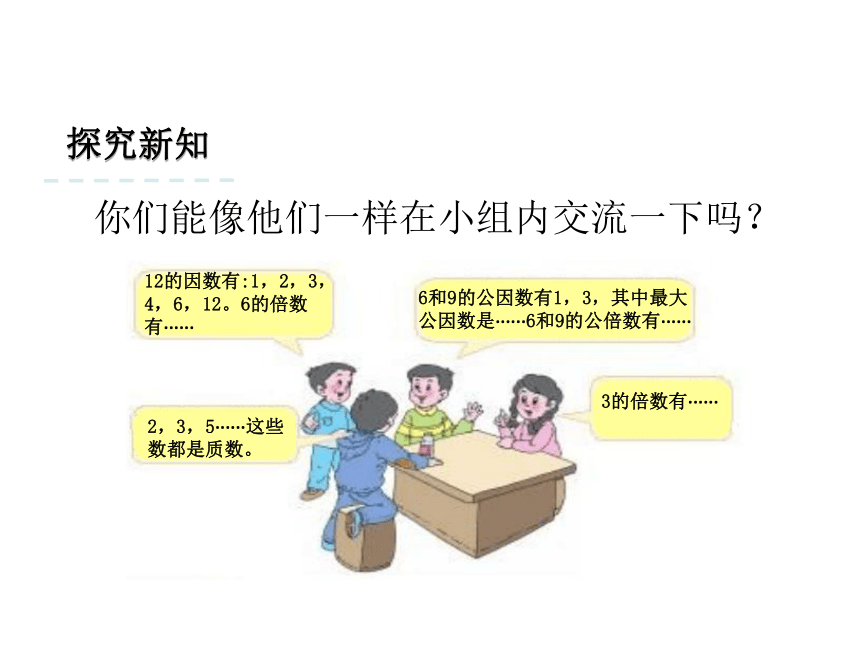
课件27张PPT。 第 2 课时 数 的 认 识(2) 第 五 单元 总复习 1. 数与代数情境导入同学们,上节课我们复习了数的认识的有关知识,这节课我们继续复习与数有关的知识。探究新知结合表中的数议一议。探究新知12的因数有:1,2,3,4,6,12。6的倍数有······2,3,5······这些数都是质数。3的倍数有······6和9的公因数有1,3,其中最大公因数是······6和9的公倍数有······你们能像他们一样在小组内交流一下吗?
例如:4×5=20,4和5是20的因数,20是4和5的倍数。探究新知交流发现
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
几个数公有的因数叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数。探究新知
几个数公有的倍数叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
交流发现个位上是0,2,4,6,8的数是2的倍数,个位上是0或5的数是5的倍数,一个数各个数位上的数字的和是3的倍数这个数就是3的倍数。探究新知
一个数各个数位上的数字的和是3的倍数,且个位上是0,这个数一定同时是2、5、3的倍数。不是2的倍数的数叫做奇数,是2的倍数的数叫做偶数。交流发现一个数只有1和它本身两个因数,这样的数叫做质数。一个数除了1和它本身以外还有别的因数,这样的数叫做合数。探究新知
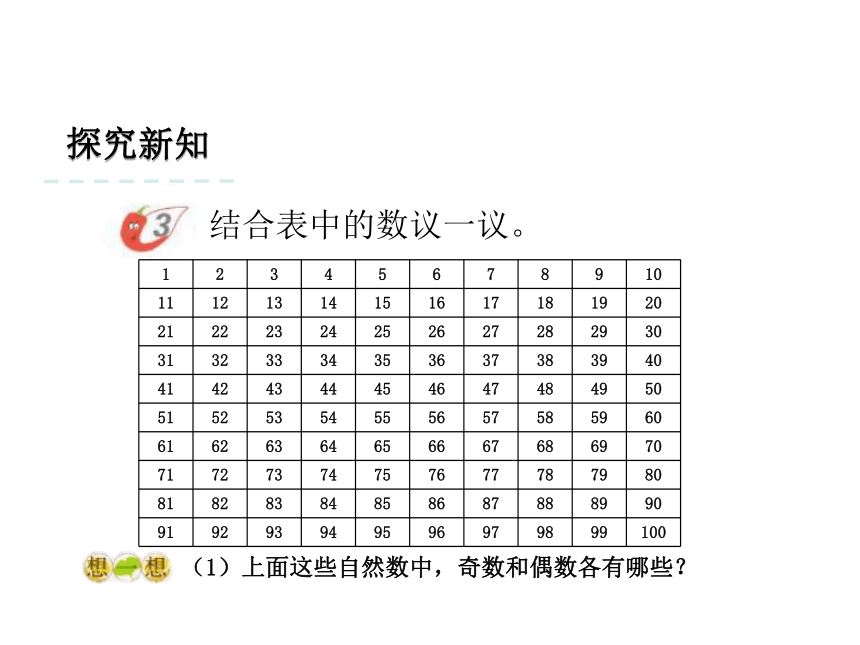
1只有它本身一个因数,所以,1既不是质数,也不是合数。最小的质数是2,最小的合数是4。交流发现探究新知结合表中的数议一议。(1)上面这些自然数中,奇数和偶数各有哪些?探究新知结合表中的数议一议。(2)什么样的数可以分解质因数,在上表中找出一个这样的数分解质因数。合数 12=2×2×3探究新知结合表中的数议一议。(1)在表中圈出2和5的公倍数。探究新知结合表中的数议一议。(2)在表中找出3和5的公倍数,并涂成红色。探究新知结合表中的数议一议。(3)在表中划出既是质数又是偶数的数;
划出既不是质数,又不是合数的数。课堂活动在直线上面的□填分数下面的□填整数或小数,并说一说分数与小数的联系。-10.51.5??课堂活动填一填。议一议:小数点位置移动,小数大小会发生怎样的变化?左移一位,缩小到原来的 ;
左移两位,缩小到原来的 ;
左移三位,缩小到原来的 ;
… …右移一位,扩大10倍;
右移两位,扩大100倍;
右移三位,扩大1000倍;
… …???典题精讲解题思路:此题考查的是用求最小公倍数的方法解决实际问题的能力,根据题意,假设这袋糖果多一块,则平均分给4个、5个或6个小朋友都能正好分完,也就是这一袋糖果加上一块,正好是4、5、6的公倍数,求这袋糖果至少有多少块就是求4、5、6的最小公倍数减1。一袋糖果,如果平均分给4个小朋友,还剩3块,如果平均分给5个小朋友,还缺1块,如果平均分给6个小朋友,还缺1块,这袋糖果至少有多少块?典题精讲解答:4、5、6的最小公倍数是60。
60-1=59(块)
答:这袋糖果至少有59块。一袋糖果,如果平均分给4个小朋友,还剩3块,如果平均分给5个小朋友,还缺1块,如果平均分给6个小朋友,还缺1块,这袋糖果至少有多少块?易错提醒判断:自然数可以分为质数和合数。(√)易错分析:错在对质数、合数的概念理解不透彻,一个数只有1和它本身两个因数,这样的数叫做质数。一个数除了1和它本身以外还有别的因数,这样的数叫做合数。因为0、1也是自然数,不属于质数和合数。易错提醒判断:自然数可以分为质数和合数。(√)正确解答:×。因为0、1也是自然数,不属于质数和合数。学以致用4和8是32的( )数
30是5和6的( )数
( )和( )是72的因数
45是( )和( )的倍数1.认识倍数与因数的关系因倍61259学以致用 写出1-20的奇数( )
写出1-20的偶数( )
最小的奇数是( ),最小的偶数是( )2.认识奇数和偶数1,3,5,7,9,11,13,15,17,19。2,4,6,8,10,12,14,16,18,20。10学以致用 写出1-20的质数( )
写出1-20的合数( )
最小的质数是( ),最小的合数是( )
3.认识质数和合数3,5,7, 11,13,17,19。2,4,6,8,9,10,12,14,15,16,18,20。24学以致用(1) 一个数的因数都比这个数的倍数小。 ( ? )
(2)1是所有自然数的公因数。 ( )
(3)含有因数2的数一定是偶数。 ( )
(4)所有的自然数不是偶数就是奇数。 ( )
(5)所有的自然数不是质数就是合数。 ( )
(6)所有的奇数都是质数,所有的偶数都是合数。( )
(7)有公因数1的两个数叫做互质数。 ( )
(8)质数除了1以外,再没有别的因数。( ) 4.我会辨。×√√√××××学以致用5.解决问题。一张长方形的纸,长1.36米,宽0.8米,把它裁成同样大小的正方形,并使它们的面积尽可能的大且裁完后没有剩余,则一共可以裁出多少张?把长方形纸剪成正方形,且没有剩余,则正方形的边长为长方形长与宽的公因数,要使正方形的面积尽可能大,所以正方形的边长是长方形长与宽的最大公因数,计算时先将米化成厘米后再求最大正方形的边长,最后求出张数。分析:学以致用5.解决问题。一张长方形的纸,长1.36米,宽0.8米,把它裁成同样大小的正方形,并使它们的面积尽可能的大且裁完后没有剩余,则一共可以裁出多少张?1.36米=136厘米 0.8米=80厘米
136和80的最大公因数是8。
(136÷8)×(80÷8)
=17×10
=170(张)
答:一共可以裁出170张。解答:课堂 总结通过这节课的学习,你学会了什么?复习了有关倍数和因数的知识,进一步明确奇数和偶数、质数与合数、公因数与公倍数的联系与区别,并能解决实际问题。
例如:4×5=20,4和5是20的因数,20是4和5的倍数。探究新知交流发现
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
几个数公有的因数叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数。探究新知
几个数公有的倍数叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
交流发现个位上是0,2,4,6,8的数是2的倍数,个位上是0或5的数是5的倍数,一个数各个数位上的数字的和是3的倍数这个数就是3的倍数。探究新知
一个数各个数位上的数字的和是3的倍数,且个位上是0,这个数一定同时是2、5、3的倍数。不是2的倍数的数叫做奇数,是2的倍数的数叫做偶数。交流发现一个数只有1和它本身两个因数,这样的数叫做质数。一个数除了1和它本身以外还有别的因数,这样的数叫做合数。探究新知
1只有它本身一个因数,所以,1既不是质数,也不是合数。最小的质数是2,最小的合数是4。交流发现探究新知结合表中的数议一议。(1)上面这些自然数中,奇数和偶数各有哪些?探究新知结合表中的数议一议。(2)什么样的数可以分解质因数,在上表中找出一个这样的数分解质因数。合数 12=2×2×3探究新知结合表中的数议一议。(1)在表中圈出2和5的公倍数。探究新知结合表中的数议一议。(2)在表中找出3和5的公倍数,并涂成红色。探究新知结合表中的数议一议。(3)在表中划出既是质数又是偶数的数;
划出既不是质数,又不是合数的数。课堂活动在直线上面的□填分数下面的□填整数或小数,并说一说分数与小数的联系。-10.51.5??课堂活动填一填。议一议:小数点位置移动,小数大小会发生怎样的变化?左移一位,缩小到原来的 ;
左移两位,缩小到原来的 ;
左移三位,缩小到原来的 ;
… …右移一位,扩大10倍;
右移两位,扩大100倍;
右移三位,扩大1000倍;
… …???典题精讲解题思路:此题考查的是用求最小公倍数的方法解决实际问题的能力,根据题意,假设这袋糖果多一块,则平均分给4个、5个或6个小朋友都能正好分完,也就是这一袋糖果加上一块,正好是4、5、6的公倍数,求这袋糖果至少有多少块就是求4、5、6的最小公倍数减1。一袋糖果,如果平均分给4个小朋友,还剩3块,如果平均分给5个小朋友,还缺1块,如果平均分给6个小朋友,还缺1块,这袋糖果至少有多少块?典题精讲解答:4、5、6的最小公倍数是60。
60-1=59(块)
答:这袋糖果至少有59块。一袋糖果,如果平均分给4个小朋友,还剩3块,如果平均分给5个小朋友,还缺1块,如果平均分给6个小朋友,还缺1块,这袋糖果至少有多少块?易错提醒判断:自然数可以分为质数和合数。(√)易错分析:错在对质数、合数的概念理解不透彻,一个数只有1和它本身两个因数,这样的数叫做质数。一个数除了1和它本身以外还有别的因数,这样的数叫做合数。因为0、1也是自然数,不属于质数和合数。易错提醒判断:自然数可以分为质数和合数。(√)正确解答:×。因为0、1也是自然数,不属于质数和合数。学以致用4和8是32的( )数
30是5和6的( )数
( )和( )是72的因数
45是( )和( )的倍数1.认识倍数与因数的关系因倍61259学以致用 写出1-20的奇数( )
写出1-20的偶数( )
最小的奇数是( ),最小的偶数是( )2.认识奇数和偶数1,3,5,7,9,11,13,15,17,19。2,4,6,8,10,12,14,16,18,20。10学以致用 写出1-20的质数( )
写出1-20的合数( )
最小的质数是( ),最小的合数是( )
3.认识质数和合数3,5,7, 11,13,17,19。2,4,6,8,9,10,12,14,15,16,18,20。24学以致用(1) 一个数的因数都比这个数的倍数小。 ( ? )
(2)1是所有自然数的公因数。 ( )
(3)含有因数2的数一定是偶数。 ( )
(4)所有的自然数不是偶数就是奇数。 ( )
(5)所有的自然数不是质数就是合数。 ( )
(6)所有的奇数都是质数,所有的偶数都是合数。( )
(7)有公因数1的两个数叫做互质数。 ( )
(8)质数除了1以外,再没有别的因数。( ) 4.我会辨。×√√√××××学以致用5.解决问题。一张长方形的纸,长1.36米,宽0.8米,把它裁成同样大小的正方形,并使它们的面积尽可能的大且裁完后没有剩余,则一共可以裁出多少张?把长方形纸剪成正方形,且没有剩余,则正方形的边长为长方形长与宽的公因数,要使正方形的面积尽可能大,所以正方形的边长是长方形长与宽的最大公因数,计算时先将米化成厘米后再求最大正方形的边长,最后求出张数。分析:学以致用5.解决问题。一张长方形的纸,长1.36米,宽0.8米,把它裁成同样大小的正方形,并使它们的面积尽可能的大且裁完后没有剩余,则一共可以裁出多少张?1.36米=136厘米 0.8米=80厘米
136和80的最大公因数是8。
(136÷8)×(80÷8)
=17×10
=170(张)
答:一共可以裁出170张。解答:课堂 总结通过这节课的学习,你学会了什么?复习了有关倍数和因数的知识,进一步明确奇数和偶数、质数与合数、公因数与公倍数的联系与区别,并能解决实际问题。
