【总结】特殊平行四边形—轴对称求最短路径
文档属性
| 名称 | 【总结】特殊平行四边形—轴对称求最短路径 |

|
|
| 格式 | doc | ||
| 文件大小 | 904.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-01 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
【总结】特殊平行四边形—轴对称求最短路径
◆知识点回顾◆
例题引入,知识点讲解
★1.例题引入
(2016年 金乡县期中)如图,直线l是 ( http: / / www.21cnjy.com )一条河,P,Q两地在直线l的同侧,欲在l上的某点M处修建一个水泵站,分别向P,Q两地供水.现有如下四种铺设方案,则铺设的管道最短的方案是( )21cnjy.comwww-2-1-cnjy-com
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.
【解答】解:作点P关于直线l的对称点P′,连接QP′交直线l于M.
根据两点之间,线段最短,可知选项B修建的管道,则所需管道最短.
故选B.
【点评】本题考查了最短路径的数学问题.这类 ( http: / / www.21cnjy.com )问题的解答依据是“两点之间,线段最短”.由于所给的条件的不同,解决方法和策略上又有所差别.【来源:21·世纪·教育·网】
★2.知识点讲解
问题模型:在直线l的同侧,有两点P,Q,在直线l上找一点M使得PM+PQ的值最小.
问题分析:在直线l上的任意一点与P,Q分别连接得到的线段长之和不同,如下图. ( http: / / www.21cnjy.com )
问题解决:作点P关于直线l的对称点P′,连 ( http: / / www.21cnjy.com )接QP′交直线l于M.在直线l上,任意取一点M’,连接PM’和QM’,求证: PM+QM≤PM’+QM’.【版权所有:21教育】
证明:因为P与P’关于直线l对称,则PM=P’M,PM’=P’M’,
当M’与M重合时,PM+QM=PM’+QM’;
当M’与M不重合时,
根据两点之间,线段最短,可知P’Q< PM’+QM’,
因为P’Q=P’M+MQ=PM+MQ,
所以PM+QM综上,由于点M’的任意性,可知当M为P’Q与直线l的交点时,PM+QM的长最短.
( http: / / www.21cnjy.com )
在学习“特殊平行四边形”时 ( http: / / www.21cnjy.com ),我们经常会遇到与最短路径的问题,同学们往往在处理这类问题时感到困难.这类问题通常会运用“轴对称”转化成“两点之间,线段最短”来解决.
下面再通过几个最短路径问题的分析,帮助同学们熟悉并掌握这类问题的解题策略,真正能做到融会贯通,一通百通.21教育网
◆经典题型讲解&变式训练◆
从易到难,丰富题型,变式训练,掌握方法。
★题型1
【题型说明:最基本的“两定点,一定直线(找第三点)”模型】
【解决方法:任选一定点,作关于定直线的对称点,将它与另一定点相连接的线段为最短路线】
(2017 岱岳区模拟)如图,正方形A ( http: / / www.21cnjy.com )BCD的边长为8,点M在边DC上,且DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
( http: / / www.21cnjy.com )
A.8 B.8 C.2 D.10
【分析】要使DN+MN最小,首先应 ( http: / / www.21cnjy.com )分析点N的位置.根据正方形的性质:正方形的对角线互相垂直平分.知点D的对称点是点B,连接MB交AC于点N,此时DN+MN最小值即是BM的长.21·世纪*教育网21*cnjy*com
【解答】解:根据题意,连接BD、BM,则BM就是所求DN+MN的最小值,
( http: / / www.21cnjy.com )
在Rt△BCM中,BC=8,CM=6
根据勾股定理得:BM==10,
即DN+MN的最小值是10;
故选D.
【点评】此题考查轴对称问题,此题的 ( http: / / www.21cnjy.com )难点在于确定满足条件的点N的位置:利用轴对称的方法.然后熟练运用勾股定理.21世纪教育网21-cn-jy.com
★变式训练1
(2016年 云梦县期末)如图,在菱形ABC ( http: / / www.21cnjy.com )D中,AB=6,∠ABC=60°,M为AD中点,P为对角线BD上一动点,连结PA和PM,则PA+PM的值最小是( )
(请写出必要过程)
( http: / / www.21cnjy.com )
A.3 B.2 C.3 D.6
★变式训练2
(2016 河南模拟)小明 ( http: / / www.21cnjy.com )是我校手工社团的一员,他在做折纸手工,如图所示在矩形ABCD中,AB=6,BC=8,点E是BC的中点,点F是边CD上的任意一点,△AEF的周长最小时,则DF的长为( )(请写出必要过程)
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
★变式训练3
(2016 扬中市一模) ( http: / / www.21cnjy.com )如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )(请写出必要过程)21教育网21*cnjy*com
( http: / / www.21cnjy.com )
A. B.3 C.4 D.
~~~~~~~~~~~~~~~~~~~~~~题型1——变式训练答案~~~~~~~~~~~~~~~~~~~~~~
变式训练1答案
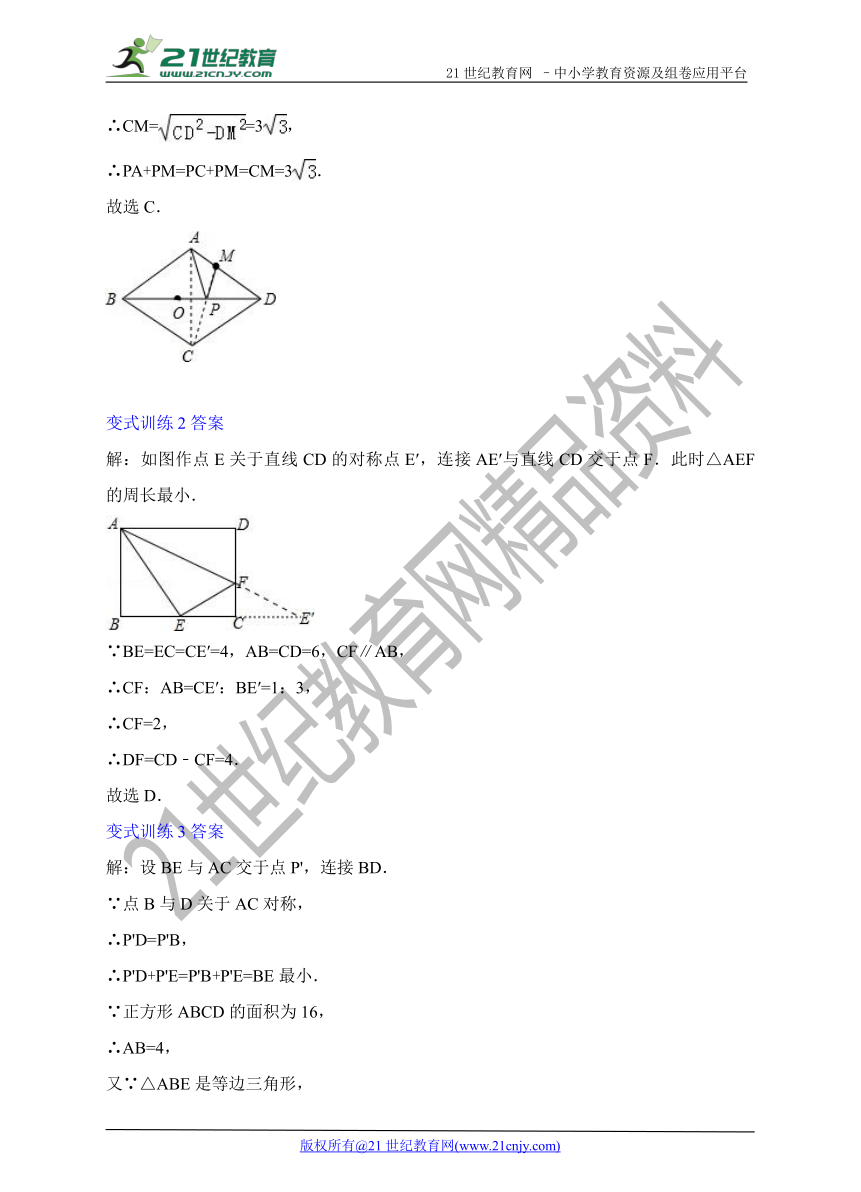
解:连接AC,交BD于点O,连接CM, ( http: / / www.21cnjy.com )则CM与BD交于点P,此时PA+PM的值最小,∵在菱形ABCD中,AB=6,∠ABC=60°,21*cnjy*com21·世纪*教育网
∴∠ADC=∠ABC=60°,AD=CD=6,BD垂直平分AC,
∴△ACD是等边三角形,PA=PC,
∵M为AD中点,
∴DM=AD=3,CM⊥AD,
∴CM==3,
∴PA+PM=PC+PM=CM=3.
故选C.
( http: / / www.21cnjy.com )
变式训练2答案
解:如图作点E关于直线CD的对称点E′,连接AE′与直线CD交于点F.此时△AEF的周长最小.
( http: / / www.21cnjy.com )
∵BE=EC=CE′=4,AB=CD=6,CF∥AB,
∴CF:AB=CE′:BE′=1:3,
∴CF=2,
∴DF=CD﹣CF=4.
故选D.
变式训练3答案
解:设BE与AC交于点P',连接BD.
∵点B与D关于AC对称,
∴P'D=P'B,
∴P'D+P'E=P'B+P'E=BE最小.
∵正方形ABCD的面积为16,
∴AB=4,
又∵△ABE是等边三角形,
∴BE=AB=4.
故选C.
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
★题型2
【题型说明: “一定点,一动点,一定直线(找第三点)”模型】
【解决方法:确定“动点”的运动路径,再作定点关于定直线的对称点,将它与动点所在的运动路径所有连线中最短的线段,就是所求的最短路径】
例1(2016年 无锡期末)如图,菱形ABCD中,∠D=135°,AD=6,CE=2,点P是线段AC上一点,点F是线段AB上一动点,则PE+PF的最小值是( )
( http: / / www.21cnjy.com )
A.3 B.6 C.2 D.3
【分析】先作点E关于AC的对称点点G, ( http: / / www.21cnjy.com )再连接BG,过点B作BH⊥CD于H,运用勾股定理求得BH和GH的长,最后在Rt△BHG中,运用勾股定理求得BG的长,即为PE+PF的最小值.21教育名师原创作品21世纪教育网版权所有
【解答】解:作点E关于AC的对称点点G,连接PG、PE,则PE=PG,CE=CG=2,
连接BG,过点B作BH⊥CD于H,则∠BCH=∠CBH=45°,
∴Rt△BHC中,BH=CH==3,
∴HG=3﹣2=,
∴Rt△BHG中,BG===2,
∵当点F与点B重合时,PE+PF=PG+PB=BG(最短),
∴PE+PF的最小值是2.
故选(C)
( http: / / www.21cnjy.com )
【点评】本题以最短距离问题为背景, ( http: / / www.21cnjy.com )主要考查了菱形的性质与轴对称的性质,凡是涉及最短距离的问题,一般要考虑线段的性质定理,一般情况要作点关于某直线的对称点.注意:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.【版权所有:21教育】www.21-cn-jy.com
例2(2016 启东市一模)如图,正方形 ( http: / / www.21cnjy.com )ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
【分析】首先作出点D关于BC的对称点 ( http: / / www.21cnjy.com )D′从而可知当点P、M、D′在一条直线上时,路径最短,当点E与点D重合,点F与点C重合时,PG和GD′均最短,即PD′最短,然后由正方形的性质和轴对称图形的性质可知:PG=1,GD′=3,最后由勾股定理即可求得PD′的长,从而可求得MD+MP的最小值.【来源:21·世纪·教育·网】
【解答】解:如图作点D关于BC的对称点D′,连接PD′,
( http: / / www.21cnjy.com )
由轴对称的性质可知:MD=D′M,CD=CD′=2
∴PM+DM=PM+MD′=PD′
过点P作PE垂直DC,垂足为G,
易证AF⊥BE,故可知P的轨迹为以AB为直径的四分之一圆弧上,当点E与点D重合,点F与点C重合时,PG和GD′均最短,
∴此时,PD′最短.
∵四边形ABCD为正方形,
∴PG=,GC=.
∴GD′=3.
在Rt△PGD′中,由勾股定理得:PD′==.
故答案为:.
【点评】本题主要考查的是最短路径问题,由轴对称图形的性质和正方形的性质确定出点P的位置是解题的关键.
★变式训练1
(2015 惠山区一模)如图,矩形AB ( http: / / www.21cnjy.com )CD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 .(请写出必要过程)
( http: / / www.21cnjy.com )
★变式训练2
(2015 泰安模拟)如图,正 ( http: / / www.21cnjy.com )方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是 .
(请写出必要过程)
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~题型2——变式训练答案~~~~~~~~~~~~~~~~~~~~~~
变式训练1答案
解:∵EF=2,点G为EF的中点,
∴DG=1,
∴G是以D为圆心,以1为半径的圆弧上的点,
作A关于BC的对称点A′,连接A′D, ( http: / / www.21cnjy.com )交BC于P,交以D为圆心,以1为半径的圆于G,此时PA+PG的值最小,最小值为A′G的长;2-1-c-n-j-y
∵AB=2,AD=3,
∴AA′=4,
∴A′D=5,
∴A′G=A′D﹣DG=5﹣1=4;
∴PA+PG的最小值为4;
故答案为4.
( http: / / www.21cnjy.com )
变式训练2答案
解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=2,
即DQ+PQ的最小值为2,
故答案为:2.
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
★题型3
【题型说明: “四点”模型:求四点构成的四边形的周长最小问题】
【解决方法:具体参考例题的解法】
(2016 济宁二模)在平面直角坐标系中, ( http: / / www.21cnjy.com )矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )21世纪21世纪教育网有21·cn·jy·com
( http: / / www.21cnjy.com )
A.(,0) B.(,0) C.(,0) D.(2,0)
【分析】将点B向右平移2个单 ( http: / / www.21cnjy.com )位得到B′(4,4),作点D关于x轴的对称点D′(0,﹣2),连接B′C′与x轴的交点为E,此时四边形BDEF周长最小,求出直线B′D′的解析式即可解决问题.21·cn·jy·com2-1-c-n-j-y
【解答】解:如图,将点B向右平移2个单 ( http: / / www.21cnjy.com )位得到B′(4,4),作点D关于x轴的对称点D′(0,﹣2),连接B′C′与x轴的交点为E,此时四边形BDEF周长最小,2·1·c·n·j·y【来源:21cnj*y.co*m】
理由∵四边形BDEF的周长为BD+DE+EF+BF,BD与EF是定值,
∴BF+DE最小时,四边形BDEF周长最小,
∵BF+ED=B′E+ED′=B′D′
设直线B′D′为y=kx+b,把(4,4),(0,﹣2)代入得解得,
∴直线B′D′为y=x﹣2,
令y=0,得x=,
∴点E坐标(,0).
故选B.
( http: / / www.21cnjy.com )
【点评】本题考查轴对称﹣最短问题、坐标 ( http: / / www.21cnjy.com )与图形性质、一次函数等知识,解题的关键是正确找到点E、F的位置,利用一次函数解决交点坐标问题,是数形结合的好题目,属于中考常考题型.【来源:21cnj*y.co*m】21教育名师原创作品
★变式训练1
如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为的线段MN在AC上运动,当四边形BMNE的周长最小时,请在图中作出此时MN的位置.
( http: / / www.21cnjy.com )
★变式训练2
如图,矩形ABCD中,AB=8,BC=16,E为CD的中点,点P、Q为BC上两个动点,
1 若连结AP、PE,则PE+AP最小值为 ;
2 连结PA、QE,若PQ=6,求四边形APQE的周长最小.
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~题型3——变式训练答案~~~~~~~~~~~~~~~~~~~~~~
变式训练1答案
解:过E作AC的平行线,且EF=,连接DF交AC于M,因为MN=,所以N确定下来,连接BM,此时BMNE的周长最小.21*cnjy*com
( http: / / www.21cnjy.com )
变式训练2答案
解:①如图1,延长AB到M,使BM=AB=8,则A和M关于BC对称,连接EM交BC于P,此时AP+EP的值最小,AP+PE=EM,
作EN⊥AB,
∴EN=AD=16,BN=AB=4,BM=AB=8,
∴MN=12,
∴EM===20.
3 如图2,点E向在平移6个单位到F,
点A关于BC的对称点A’,
连接AF,交BC于P,此时AP+QE=A’P+PF=A’F最小,
∴此时,四边形APQE的周长最小,延长E ( http: / / www.21cnjy.com )F交AB于G,则EG与AB垂直,且EG=AB=16,则GF=10,A’G=A’B+BG=4+8=12,【出处:21教育名师】
则AF=.
又因为DE=
则周长最小为.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
★题型4
【题型说明: 特殊平行四边形其他求最短路径或周长】
【解决方法:运用垂线最短】
(2016春 杭州期末)如图,菱形ABCD中 ( http: / / www.21cnjy.com ),AB=4,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°,则△BEF周长的最小值是( )【出处:21教育名师】
( http: / / www.21cnjy.com )
A.6 B.4 C.4+ D.4+2
【分析】只要证明△DBE≌△DCF得 ( http: / / www.21cnjy.com )出△DEF是等边三角形,因为△BEF的周长=BE+BF+EF=BF+CF+EF=BC+EF=4+EF,所以等边三角形△DEF的边长最小时,△BEF的周长最小,只要求出△DEF的边长最小值即可.www-2-1-cnjy-com
【解答】解:在△BDE和△CDF中,
,
∴△DBE≌△DCF,
∴DE=DF,∠BDE=∠CDF,BE=CF,
∴∠EDF=∠BDC=60°,
∴△DEF是等边三角形,
∵△BEF的周长=BE+BF+EF=BF+CF+EF=BC+EF=4+EF,
∴等边三角形△DEF的边长最小时,△BEF的周长最小,
当DE⊥AB时,DE最小=2,
∴△BEF的周长最小值为4+2,
故选D.
【点评】本题考查菱形的性质、全等三角形 ( http: / / www.21cnjy.com )的判定和性质、等边三角形的判定和性质、最小值问题等知识,解题的关键是正确寻找全等三角形,利用全等三角形的性质解决问题,学会转化的思想解决问题,所以中考常考题型.
★变式训练
(2016 深圳模拟)如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是 4 .
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~题型4——变式训练答案~~~~~~~~~~~~~~~~~~~~~~
变式训练答案
解:以CD为轴,将△ACD往上翻转180°,如图,
( http: / / www.21cnjy.com )
过点A作AE⊥A′C于E点,AE交CD于F点,
当Q与F点重合,P′与E点重合时,AQ+QP=AF+EF=AE最短(直线外一点到这条直线中,垂线段最短),21cnjy.com
∵矩形ABCD中,AD=4,∠CAB=30°,
∴∠A′CD=∠ACD=∠CAB=30°,
∴∠A′CA=60°,
又∵AC=A′C,
∴△A′CA为等边三角形,且A′A=2AD=8,
AE= 8×=4.
故答案为:4.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
【总结】特殊平行四边形—轴对称求最短路径
◆知识点回顾◆
例题引入,知识点讲解
★1.例题引入
(2016年 金乡县期中)如图,直线l是 ( http: / / www.21cnjy.com )一条河,P,Q两地在直线l的同侧,欲在l上的某点M处修建一个水泵站,分别向P,Q两地供水.现有如下四种铺设方案,则铺设的管道最短的方案是( )21cnjy.comwww-2-1-cnjy-com
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【分析】用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.
【解答】解:作点P关于直线l的对称点P′,连接QP′交直线l于M.
根据两点之间,线段最短,可知选项B修建的管道,则所需管道最短.
故选B.
【点评】本题考查了最短路径的数学问题.这类 ( http: / / www.21cnjy.com )问题的解答依据是“两点之间,线段最短”.由于所给的条件的不同,解决方法和策略上又有所差别.【来源:21·世纪·教育·网】
★2.知识点讲解
问题模型:在直线l的同侧,有两点P,Q,在直线l上找一点M使得PM+PQ的值最小.
问题分析:在直线l上的任意一点与P,Q分别连接得到的线段长之和不同,如下图. ( http: / / www.21cnjy.com )
问题解决:作点P关于直线l的对称点P′,连 ( http: / / www.21cnjy.com )接QP′交直线l于M.在直线l上,任意取一点M’,连接PM’和QM’,求证: PM+QM≤PM’+QM’.【版权所有:21教育】
证明:因为P与P’关于直线l对称,则PM=P’M,PM’=P’M’,
当M’与M重合时,PM+QM=PM’+QM’;
当M’与M不重合时,
根据两点之间,线段最短,可知P’Q< PM’+QM’,
因为P’Q=P’M+MQ=PM+MQ,
所以PM+QM
( http: / / www.21cnjy.com )
在学习“特殊平行四边形”时 ( http: / / www.21cnjy.com ),我们经常会遇到与最短路径的问题,同学们往往在处理这类问题时感到困难.这类问题通常会运用“轴对称”转化成“两点之间,线段最短”来解决.
下面再通过几个最短路径问题的分析,帮助同学们熟悉并掌握这类问题的解题策略,真正能做到融会贯通,一通百通.21教育网
◆经典题型讲解&变式训练◆
从易到难,丰富题型,变式训练,掌握方法。
★题型1
【题型说明:最基本的“两定点,一定直线(找第三点)”模型】
【解决方法:任选一定点,作关于定直线的对称点,将它与另一定点相连接的线段为最短路线】
(2017 岱岳区模拟)如图,正方形A ( http: / / www.21cnjy.com )BCD的边长为8,点M在边DC上,且DM=2,点N是边AC上一动点,则线段DN+MN的最小值为( )
( http: / / www.21cnjy.com )
A.8 B.8 C.2 D.10
【分析】要使DN+MN最小,首先应 ( http: / / www.21cnjy.com )分析点N的位置.根据正方形的性质:正方形的对角线互相垂直平分.知点D的对称点是点B,连接MB交AC于点N,此时DN+MN最小值即是BM的长.21·世纪*教育网21*cnjy*com
【解答】解:根据题意,连接BD、BM,则BM就是所求DN+MN的最小值,
( http: / / www.21cnjy.com )
在Rt△BCM中,BC=8,CM=6
根据勾股定理得:BM==10,
即DN+MN的最小值是10;
故选D.
【点评】此题考查轴对称问题,此题的 ( http: / / www.21cnjy.com )难点在于确定满足条件的点N的位置:利用轴对称的方法.然后熟练运用勾股定理.21世纪教育网21-cn-jy.com
★变式训练1
(2016年 云梦县期末)如图,在菱形ABC ( http: / / www.21cnjy.com )D中,AB=6,∠ABC=60°,M为AD中点,P为对角线BD上一动点,连结PA和PM,则PA+PM的值最小是( )
(请写出必要过程)
( http: / / www.21cnjy.com )
A.3 B.2 C.3 D.6
★变式训练2
(2016 河南模拟)小明 ( http: / / www.21cnjy.com )是我校手工社团的一员,他在做折纸手工,如图所示在矩形ABCD中,AB=6,BC=8,点E是BC的中点,点F是边CD上的任意一点,△AEF的周长最小时,则DF的长为( )(请写出必要过程)
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
★变式训练3
(2016 扬中市一模) ( http: / / www.21cnjy.com )如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )(请写出必要过程)21教育网21*cnjy*com
( http: / / www.21cnjy.com )
A. B.3 C.4 D.
~~~~~~~~~~~~~~~~~~~~~~题型1——变式训练答案~~~~~~~~~~~~~~~~~~~~~~
变式训练1答案
解:连接AC,交BD于点O,连接CM, ( http: / / www.21cnjy.com )则CM与BD交于点P,此时PA+PM的值最小,∵在菱形ABCD中,AB=6,∠ABC=60°,21*cnjy*com21·世纪*教育网
∴∠ADC=∠ABC=60°,AD=CD=6,BD垂直平分AC,
∴△ACD是等边三角形,PA=PC,
∵M为AD中点,
∴DM=AD=3,CM⊥AD,
∴CM==3,
∴PA+PM=PC+PM=CM=3.
故选C.
( http: / / www.21cnjy.com )
变式训练2答案
解:如图作点E关于直线CD的对称点E′,连接AE′与直线CD交于点F.此时△AEF的周长最小.
( http: / / www.21cnjy.com )
∵BE=EC=CE′=4,AB=CD=6,CF∥AB,
∴CF:AB=CE′:BE′=1:3,
∴CF=2,
∴DF=CD﹣CF=4.
故选D.
变式训练3答案
解:设BE与AC交于点P',连接BD.
∵点B与D关于AC对称,
∴P'D=P'B,
∴P'D+P'E=P'B+P'E=BE最小.
∵正方形ABCD的面积为16,
∴AB=4,
又∵△ABE是等边三角形,
∴BE=AB=4.
故选C.
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
★题型2
【题型说明: “一定点,一动点,一定直线(找第三点)”模型】
【解决方法:确定“动点”的运动路径,再作定点关于定直线的对称点,将它与动点所在的运动路径所有连线中最短的线段,就是所求的最短路径】
例1(2016年 无锡期末)如图,菱形ABCD中,∠D=135°,AD=6,CE=2,点P是线段AC上一点,点F是线段AB上一动点,则PE+PF的最小值是( )
( http: / / www.21cnjy.com )
A.3 B.6 C.2 D.3
【分析】先作点E关于AC的对称点点G, ( http: / / www.21cnjy.com )再连接BG,过点B作BH⊥CD于H,运用勾股定理求得BH和GH的长,最后在Rt△BHG中,运用勾股定理求得BG的长,即为PE+PF的最小值.21教育名师原创作品21世纪教育网版权所有
【解答】解:作点E关于AC的对称点点G,连接PG、PE,则PE=PG,CE=CG=2,
连接BG,过点B作BH⊥CD于H,则∠BCH=∠CBH=45°,
∴Rt△BHC中,BH=CH==3,
∴HG=3﹣2=,
∴Rt△BHG中,BG===2,
∵当点F与点B重合时,PE+PF=PG+PB=BG(最短),
∴PE+PF的最小值是2.
故选(C)
( http: / / www.21cnjy.com )
【点评】本题以最短距离问题为背景, ( http: / / www.21cnjy.com )主要考查了菱形的性质与轴对称的性质,凡是涉及最短距离的问题,一般要考虑线段的性质定理,一般情况要作点关于某直线的对称点.注意:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.【版权所有:21教育】www.21-cn-jy.com
例2(2016 启东市一模)如图,正方形 ( http: / / www.21cnjy.com )ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为 .2·1·c·n·j·y
( http: / / www.21cnjy.com )
【分析】首先作出点D关于BC的对称点 ( http: / / www.21cnjy.com )D′从而可知当点P、M、D′在一条直线上时,路径最短,当点E与点D重合,点F与点C重合时,PG和GD′均最短,即PD′最短,然后由正方形的性质和轴对称图形的性质可知:PG=1,GD′=3,最后由勾股定理即可求得PD′的长,从而可求得MD+MP的最小值.【来源:21·世纪·教育·网】
【解答】解:如图作点D关于BC的对称点D′,连接PD′,
( http: / / www.21cnjy.com )
由轴对称的性质可知:MD=D′M,CD=CD′=2
∴PM+DM=PM+MD′=PD′
过点P作PE垂直DC,垂足为G,
易证AF⊥BE,故可知P的轨迹为以AB为直径的四分之一圆弧上,当点E与点D重合,点F与点C重合时,PG和GD′均最短,
∴此时,PD′最短.
∵四边形ABCD为正方形,
∴PG=,GC=.
∴GD′=3.
在Rt△PGD′中,由勾股定理得:PD′==.
故答案为:.
【点评】本题主要考查的是最短路径问题,由轴对称图形的性质和正方形的性质确定出点P的位置是解题的关键.
★变式训练1
(2015 惠山区一模)如图,矩形AB ( http: / / www.21cnjy.com )CD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 .(请写出必要过程)
( http: / / www.21cnjy.com )
★变式训练2
(2015 泰安模拟)如图,正 ( http: / / www.21cnjy.com )方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是 .
(请写出必要过程)
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~题型2——变式训练答案~~~~~~~~~~~~~~~~~~~~~~
变式训练1答案
解:∵EF=2,点G为EF的中点,
∴DG=1,
∴G是以D为圆心,以1为半径的圆弧上的点,
作A关于BC的对称点A′,连接A′D, ( http: / / www.21cnjy.com )交BC于P,交以D为圆心,以1为半径的圆于G,此时PA+PG的值最小,最小值为A′G的长;2-1-c-n-j-y
∵AB=2,AD=3,
∴AA′=4,
∴A′D=5,
∴A′G=A′D﹣DG=5﹣1=4;
∴PA+PG的最小值为4;
故答案为4.
( http: / / www.21cnjy.com )
变式训练2答案
解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=2,
即DQ+PQ的最小值为2,
故答案为:2.
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
★题型3
【题型说明: “四点”模型:求四点构成的四边形的周长最小问题】
【解决方法:具体参考例题的解法】
(2016 济宁二模)在平面直角坐标系中, ( http: / / www.21cnjy.com )矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )21世纪21世纪教育网有21·cn·jy·com
( http: / / www.21cnjy.com )
A.(,0) B.(,0) C.(,0) D.(2,0)
【分析】将点B向右平移2个单 ( http: / / www.21cnjy.com )位得到B′(4,4),作点D关于x轴的对称点D′(0,﹣2),连接B′C′与x轴的交点为E,此时四边形BDEF周长最小,求出直线B′D′的解析式即可解决问题.21·cn·jy·com2-1-c-n-j-y
【解答】解:如图,将点B向右平移2个单 ( http: / / www.21cnjy.com )位得到B′(4,4),作点D关于x轴的对称点D′(0,﹣2),连接B′C′与x轴的交点为E,此时四边形BDEF周长最小,2·1·c·n·j·y【来源:21cnj*y.co*m】
理由∵四边形BDEF的周长为BD+DE+EF+BF,BD与EF是定值,
∴BF+DE最小时,四边形BDEF周长最小,
∵BF+ED=B′E+ED′=B′D′
设直线B′D′为y=kx+b,把(4,4),(0,﹣2)代入得解得,
∴直线B′D′为y=x﹣2,
令y=0,得x=,
∴点E坐标(,0).
故选B.
( http: / / www.21cnjy.com )
【点评】本题考查轴对称﹣最短问题、坐标 ( http: / / www.21cnjy.com )与图形性质、一次函数等知识,解题的关键是正确找到点E、F的位置,利用一次函数解决交点坐标问题,是数形结合的好题目,属于中考常考题型.【来源:21cnj*y.co*m】21教育名师原创作品
★变式训练1
如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为的线段MN在AC上运动,当四边形BMNE的周长最小时,请在图中作出此时MN的位置.
( http: / / www.21cnjy.com )
★变式训练2
如图,矩形ABCD中,AB=8,BC=16,E为CD的中点,点P、Q为BC上两个动点,
1 若连结AP、PE,则PE+AP最小值为 ;
2 连结PA、QE,若PQ=6,求四边形APQE的周长最小.
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~题型3——变式训练答案~~~~~~~~~~~~~~~~~~~~~~
变式训练1答案
解:过E作AC的平行线,且EF=,连接DF交AC于M,因为MN=,所以N确定下来,连接BM,此时BMNE的周长最小.21*cnjy*com
( http: / / www.21cnjy.com )
变式训练2答案
解:①如图1,延长AB到M,使BM=AB=8,则A和M关于BC对称,连接EM交BC于P,此时AP+EP的值最小,AP+PE=EM,
作EN⊥AB,
∴EN=AD=16,BN=AB=4,BM=AB=8,
∴MN=12,
∴EM===20.
3 如图2,点E向在平移6个单位到F,
点A关于BC的对称点A’,
连接AF,交BC于P,此时AP+QE=A’P+PF=A’F最小,
∴此时,四边形APQE的周长最小,延长E ( http: / / www.21cnjy.com )F交AB于G,则EG与AB垂直,且EG=AB=16,则GF=10,A’G=A’B+BG=4+8=12,【出处:21教育名师】
则AF=.
又因为DE=
则周长最小为.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
★题型4
【题型说明: 特殊平行四边形其他求最短路径或周长】
【解决方法:运用垂线最短】
(2016春 杭州期末)如图,菱形ABCD中 ( http: / / www.21cnjy.com ),AB=4,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°,则△BEF周长的最小值是( )【出处:21教育名师】
( http: / / www.21cnjy.com )
A.6 B.4 C.4+ D.4+2
【分析】只要证明△DBE≌△DCF得 ( http: / / www.21cnjy.com )出△DEF是等边三角形,因为△BEF的周长=BE+BF+EF=BF+CF+EF=BC+EF=4+EF,所以等边三角形△DEF的边长最小时,△BEF的周长最小,只要求出△DEF的边长最小值即可.www-2-1-cnjy-com
【解答】解:在△BDE和△CDF中,
,
∴△DBE≌△DCF,
∴DE=DF,∠BDE=∠CDF,BE=CF,
∴∠EDF=∠BDC=60°,
∴△DEF是等边三角形,
∵△BEF的周长=BE+BF+EF=BF+CF+EF=BC+EF=4+EF,
∴等边三角形△DEF的边长最小时,△BEF的周长最小,
当DE⊥AB时,DE最小=2,
∴△BEF的周长最小值为4+2,
故选D.
【点评】本题考查菱形的性质、全等三角形 ( http: / / www.21cnjy.com )的判定和性质、等边三角形的判定和性质、最小值问题等知识,解题的关键是正确寻找全等三角形,利用全等三角形的性质解决问题,学会转化的思想解决问题,所以中考常考题型.
★变式训练
(2016 深圳模拟)如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是 4 .
( http: / / www.21cnjy.com )
~~~~~~~~~~~~~~~~~~~~~~题型4——变式训练答案~~~~~~~~~~~~~~~~~~~~~~
变式训练答案
解:以CD为轴,将△ACD往上翻转180°,如图,
( http: / / www.21cnjy.com )
过点A作AE⊥A′C于E点,AE交CD于F点,
当Q与F点重合,P′与E点重合时,AQ+QP=AF+EF=AE最短(直线外一点到这条直线中,垂线段最短),21cnjy.com
∵矩形ABCD中,AD=4,∠CAB=30°,
∴∠A′CD=∠ACD=∠CAB=30°,
∴∠A′CA=60°,
又∵AC=A′C,
∴△A′CA为等边三角形,且A′A=2AD=8,
AE= 8×=4.
故答案为:4.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
