26.2 实际问题与反比例函数 同步测试(含答案)
文档属性
| 名称 | 26.2 实际问题与反比例函数 同步测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-01 17:25:59 | ||
图片预览



文档简介
26.2
实际问题与反比例函数
同步测试
一、选择题
1.反比例函数,当x<0时,y随x的增大而增大,则m的值是(
)
A.
B.
C.
或
D.
2
2.已知反比例函数的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
(
)
A.
m>0
B.
m>
C.
m<0
D.
m<
3.已知力F所作的功是15焦,则力F与物体在力的方向通过的距离S之间关系的图象大致是
4.
已知点(1,a)在反比例函数y=
(k≠0)的图象上,其中a=m2+2m+5
(m为实数),则这个函数的图象在第_________象限.(
)
A.一
B.二
C.一、三
D.二、四
5.
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:kg/m3)是体积(单位:m3)的反比例函数,它的图象如图3所示,当时,气体的密度是(
)
A.5kg/m3
B.2kg/m3
C.100kg/m3
D,1kg/m3
6.
反比例函数(为常数,)的图象位于( )
A.第一、二象限
B.第一、三象限
C.第二、四角限
D.第三、四象限
7.甲乙两地相距,汽车从甲地以(的速度开往乙地,所需时间是,则正确的是(
)
A.当为定植时,与成反比例
B.
当为定植时,与成反比例
C.当为定植时,与成反比例
D.以上三个均不正确
8.
下列两个变量之间的关系为反比例关系的是(
)
A.匀速行驶过程中,行驶路程与时间的关系
B.体积一定时,物体的质量与密度的关系
C.质量一定时,物体的体积与密度的关系
D.长方形的长一定时,它的周长与宽的关系
9.如图所示,A(,)、B(,)、C(,)是函数的图象在第一象限分支上的三个点,且<<,过A、B、C三点分别作坐标轴的垂线,得矩形ADOH、BEON、CFOP,它们的面积分别为S1、S2、S3,则下列结论中正确的是(
).
S1B.
S3
S1
C.
S2<
S3<
S1
D.
S1=S2=S3
二、填空题
10.已知点P(1,)在反比例函数的图像上,其中
(为实数),则这个函数的图像在第_______
象限.
11.正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为(),则k1k2=____________.
12.近视眼镜的度数(度)与镜片焦距(成反比例,已知400度近视眼镜镜片的焦距为0.25,则与的函数关系式为
.
13.如果点(在双曲线上,那么双曲线在
象限.
14.双曲线和一次函数的图象的两个交点分别为A(-1,-4),B(2,),则
.
15.
A、B两地之间的高速公路长为300km,一辆小汽车从A地去B
地,假设在途中是匀速直线运动,速度为vkm/h,到达时所用的时间
是th,那么t是v的
函数,t可以写成v的函数关系式
是
。
三、解答题
16.(8分)已知y
=
y1
+y2,而y1与x+1成反比例,y2与成正比例,并且时,y=2;时,y=2,求y与x的函数关系式.
17.(8分)在某一电路中,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=55欧姆时,电流I=4安培.
(1)求I与R之间的函数关系式
(2)当电流I=2安培时,求电阻R的值.
18.
如图,Rt△ABO的顶点A(a、b)是一次函数y=x+m的图像与反比例函数的图像在第一象限的交点,且S△ABO=3。
①根据这些条件你能够求出反比例函数的解析式吗?
如果能够,请你求出来,如果不能,请说明理由。
②你能够求出一次函数的函数关系式吗?如果能,请你求出来,如果不能,请你说明理由。
19.
小明在某一次实验中,测得两个变量之间的关系如下表所示:
自变量x
1
2
3
4
12
因变量y
12.03
5.98
3.04
1.99
1.00
请你根据表格回答下列问题:
①
这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由。
②请你写出这个函数的解析式。
③表格中空缺的数值可能是多少?请你给出合理的数值。
20.小刘驾车从A地到B地,每小时行驶75千米,刚好用了4小时,然后驾车返回.
(1)返回时车速为(千米/小时)所用时间为(小时).写出与之间的函数关系式;
(2)如果因有紧急情况,小刘需在3小时内返回A地,那么,返回时车速至少是多少?
21.在某一电路中,保持电压不变,电流(安培)与电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流=2安培时,
(1)求与R之间的函数关系式
(2)当电流=0.5安培时,求电阻R的值
22.某商场出售一批进价为2元的贺卡,在市场营销中发现商品的日销售单价元与日销售量个之间有如下关系:
(元)
3
4
5
6
(个)
20
15
12
10
(1)根据表中数据,在直角坐标系描出实数对()的对应点
(2)猜测并确定与之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为W元,试求出W与之间的函数关系式,若物价居规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价定为多少元时,才能获得最大日销售利润?
答案:
一、
1.
A,提示:根据反比例函数定义得到,解得,由,故选A;
2.D,提示:由当x1<0<x2时,有y1<y2,得到,故选D;
3.D,提示:根据反比例函数的性质求得;
4.D。,提示:因为y与x成反比例函数关系,三角形的底与高都必须大于0,所以x>0的图像在第一象限。
5.C,提示:因为m=ρV,当V=30时,m=30ρ,故为正比例函数。6.D,提示:其中S1=S2=S3=|k|;
7.C;
8.
D;
9.C,提示:因为则-,故在二、四象限,选C;
二、
10.二;
11.12
;
12.,提示:由于与成反比例,则,当=400时,=0.25,所以,又焦距不能为负值,故;13.二、四,提示:将点(代入得,又因为,所以图象在二、四象限;
14.-2,提示:由双曲线经过A、B得,解得=2,由经过A、B得解得,-2;
15.
反比例函数
;
三、16.
17.(1);(2)110
18.
(1).由△OAB的面积为3,可以求出反比例函数的系数为6,所以函数解析式为
(2).根据这些条件不足以求出一次函数的关系式。由于点A的坐标并不确定,所以无法确定一次函数中的m,也就不能确定一次函数的关系式。实际上一次函数与反比例函数的交点以及坐标原点所构成的三角形的面积应该是一个定值,从这点也可以看出一次函数的解析式不是唯一的。
19.
1)反比例函数
2)
3)近似于6与4即可
20.(1)设A、B两地之间的路程为千米,则=75×4=300(千米)
∴与之间的函数关系式是.
(2)当=3时,则有3=,∴返回时车速至少是100千米/小时.
21.(1)设,把R=5,I=2代入,即可求得U=10,即与R之间的函数关系式I=;
(2)当I=0.5时,0.5=(欧姆),因此电阻R的值为20欧姆..
22.(1)略;(2)设,把代入中,得分别把(4,15)(5,12),(6,10)代入上式均成立;∴与之间的函数关系式是;
(3)W=(,当时,W有最大值.
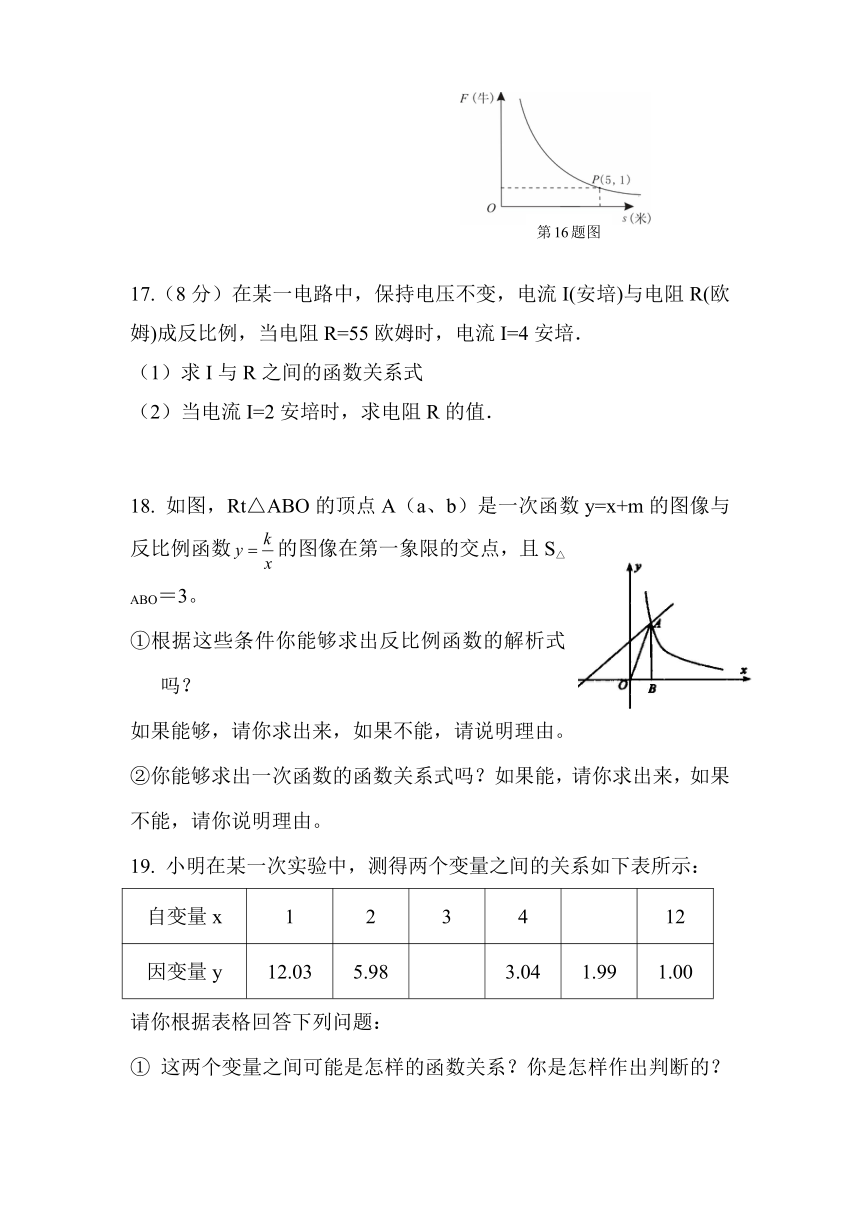
第16题图
实际问题与反比例函数
同步测试
一、选择题
1.反比例函数,当x<0时,y随x的增大而增大,则m的值是(
)
A.
B.
C.
或
D.
2
2.已知反比例函数的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
(
)
A.
m>0
B.
m>
C.
m<0
D.
m<
3.已知力F所作的功是15焦,则力F与物体在力的方向通过的距离S之间关系的图象大致是
4.
已知点(1,a)在反比例函数y=
(k≠0)的图象上,其中a=m2+2m+5
(m为实数),则这个函数的图象在第_________象限.(
)
A.一
B.二
C.一、三
D.二、四
5.
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:kg/m3)是体积(单位:m3)的反比例函数,它的图象如图3所示,当时,气体的密度是(
)
A.5kg/m3
B.2kg/m3
C.100kg/m3
D,1kg/m3
6.
反比例函数(为常数,)的图象位于( )
A.第一、二象限
B.第一、三象限
C.第二、四角限
D.第三、四象限
7.甲乙两地相距,汽车从甲地以(的速度开往乙地,所需时间是,则正确的是(
)
A.当为定植时,与成反比例
B.
当为定植时,与成反比例
C.当为定植时,与成反比例
D.以上三个均不正确
8.
下列两个变量之间的关系为反比例关系的是(
)
A.匀速行驶过程中,行驶路程与时间的关系
B.体积一定时,物体的质量与密度的关系
C.质量一定时,物体的体积与密度的关系
D.长方形的长一定时,它的周长与宽的关系
9.如图所示,A(,)、B(,)、C(,)是函数的图象在第一象限分支上的三个点,且<<,过A、B、C三点分别作坐标轴的垂线,得矩形ADOH、BEON、CFOP,它们的面积分别为S1、S2、S3,则下列结论中正确的是(
).
S1
S3
C.
S2<
S3<
S1
D.
S1=S2=S3
二、填空题
10.已知点P(1,)在反比例函数的图像上,其中
(为实数),则这个函数的图像在第_______
象限.
11.正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为(),则k1k2=____________.
12.近视眼镜的度数(度)与镜片焦距(成反比例,已知400度近视眼镜镜片的焦距为0.25,则与的函数关系式为
.
13.如果点(在双曲线上,那么双曲线在
象限.
14.双曲线和一次函数的图象的两个交点分别为A(-1,-4),B(2,),则
.
15.
A、B两地之间的高速公路长为300km,一辆小汽车从A地去B
地,假设在途中是匀速直线运动,速度为vkm/h,到达时所用的时间
是th,那么t是v的
函数,t可以写成v的函数关系式
是
。
三、解答题
16.(8分)已知y
=
y1
+y2,而y1与x+1成反比例,y2与成正比例,并且时,y=2;时,y=2,求y与x的函数关系式.
17.(8分)在某一电路中,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=55欧姆时,电流I=4安培.
(1)求I与R之间的函数关系式
(2)当电流I=2安培时,求电阻R的值.
18.
如图,Rt△ABO的顶点A(a、b)是一次函数y=x+m的图像与反比例函数的图像在第一象限的交点,且S△ABO=3。
①根据这些条件你能够求出反比例函数的解析式吗?
如果能够,请你求出来,如果不能,请说明理由。
②你能够求出一次函数的函数关系式吗?如果能,请你求出来,如果不能,请你说明理由。
19.
小明在某一次实验中,测得两个变量之间的关系如下表所示:
自变量x
1
2
3
4
12
因变量y
12.03
5.98
3.04
1.99
1.00
请你根据表格回答下列问题:
①
这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由。
②请你写出这个函数的解析式。
③表格中空缺的数值可能是多少?请你给出合理的数值。
20.小刘驾车从A地到B地,每小时行驶75千米,刚好用了4小时,然后驾车返回.
(1)返回时车速为(千米/小时)所用时间为(小时).写出与之间的函数关系式;
(2)如果因有紧急情况,小刘需在3小时内返回A地,那么,返回时车速至少是多少?
21.在某一电路中,保持电压不变,电流(安培)与电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流=2安培时,
(1)求与R之间的函数关系式
(2)当电流=0.5安培时,求电阻R的值
22.某商场出售一批进价为2元的贺卡,在市场营销中发现商品的日销售单价元与日销售量个之间有如下关系:
(元)
3
4
5
6
(个)
20
15
12
10
(1)根据表中数据,在直角坐标系描出实数对()的对应点
(2)猜测并确定与之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为W元,试求出W与之间的函数关系式,若物价居规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价定为多少元时,才能获得最大日销售利润?
答案:
一、
1.
A,提示:根据反比例函数定义得到,解得,由,故选A;
2.D,提示:由当x1<0<x2时,有y1<y2,得到,故选D;
3.D,提示:根据反比例函数的性质求得;
4.D。,提示:因为y与x成反比例函数关系,三角形的底与高都必须大于0,所以x>0的图像在第一象限。
5.C,提示:因为m=ρV,当V=30时,m=30ρ,故为正比例函数。6.D,提示:其中S1=S2=S3=|k|;
7.C;
8.
D;
9.C,提示:因为则-,故在二、四象限,选C;
二、
10.二;
11.12
;
12.,提示:由于与成反比例,则,当=400时,=0.25,所以,又焦距不能为负值,故;13.二、四,提示:将点(代入得,又因为,所以图象在二、四象限;
14.-2,提示:由双曲线经过A、B得,解得=2,由经过A、B得解得,-2;
15.
反比例函数
;
三、16.
17.(1);(2)110
18.
(1).由△OAB的面积为3,可以求出反比例函数的系数为6,所以函数解析式为
(2).根据这些条件不足以求出一次函数的关系式。由于点A的坐标并不确定,所以无法确定一次函数中的m,也就不能确定一次函数的关系式。实际上一次函数与反比例函数的交点以及坐标原点所构成的三角形的面积应该是一个定值,从这点也可以看出一次函数的解析式不是唯一的。
19.
1)反比例函数
2)
3)近似于6与4即可
20.(1)设A、B两地之间的路程为千米,则=75×4=300(千米)
∴与之间的函数关系式是.
(2)当=3时,则有3=,∴返回时车速至少是100千米/小时.
21.(1)设,把R=5,I=2代入,即可求得U=10,即与R之间的函数关系式I=;
(2)当I=0.5时,0.5=(欧姆),因此电阻R的值为20欧姆..
22.(1)略;(2)设,把代入中,得分别把(4,15)(5,12),(6,10)代入上式均成立;∴与之间的函数关系式是;
(3)W=(,当时,W有最大值.
第16题图
