浙江省宁波市2016年普通高中保送生考试数学例卷(含答案)
文档属性
| 名称 | 浙江省宁波市2016年普通高中保送生考试数学例卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 678.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-05 16:21:45 | ||
图片预览


文档简介
宁波市2016年普通高中保送生考试数学例卷
姓名__________就读初中_________________中考报名序号_________________
第Ⅰ部分
数学
一、选择题(本题有5小题,每小题5分,共25分)
1.若,,,则的值为(
)
A.
B.
C.
D.
2.函数的图象如图所示,则函数
的图象与x轴的交点分别是(
)
A.、
B.、
C.、
D.、
3.定义新运算:对于任意实数、都有.若,则关于、的方程组的解是(
)
A.
B.
C.
D.
4.已知函数,当自变量满足时,函数值的取值范围是,
则实数的取值范围是(
)
A.
B.
C.
D.
5.如图,棱长为1的正方体形状的箱子放在地面上(面ABCD着地),先将它绕着棱BC旋转90o,使得面着地;再绕着棱旋转90o,使得面着地;最后绕着棱旋转90o,使得面着地.在这个运动过程中,顶点A在空间所经过的路径长为
(
)
A.
B.
C.
D.
二、填空题(本题有4小题,每小题5分,共20分)
6.已知、、均为实数,且,,则
▲
.
7.如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
此时,他离地面的高度是
▲
米.
8.如图,一次函数y=x+1的图象交x轴于点E、交反比例函数的图象于点F(点F在第一象限),过线段EF上异于E、F的动点A作x轴的平行线交的图象于点B,过点A、B
作x轴的垂线段,垂足分别是点D、C,则矩形ABCD的面积最大值为
▲
.
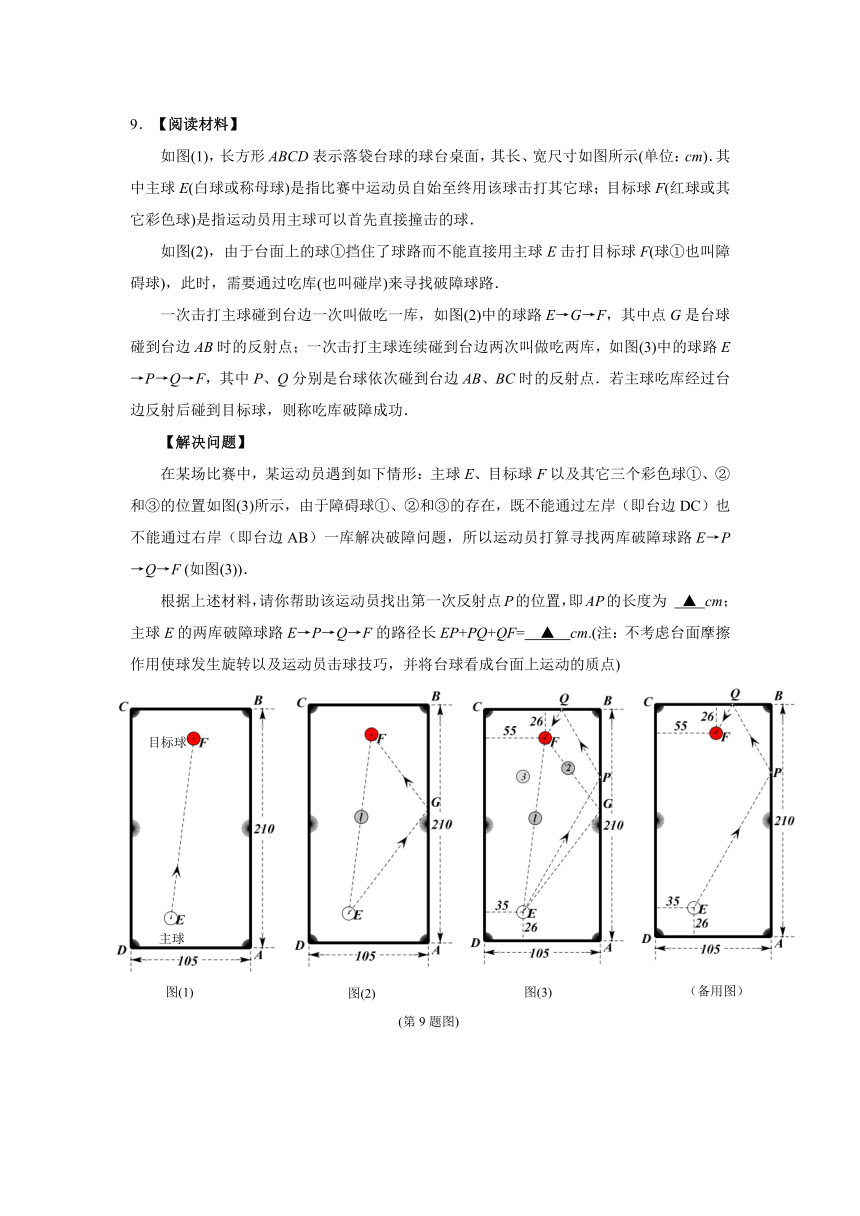
9.【阅读材料】
如图(1),长方形ABCD表示落袋台球的球台桌面,其长、宽尺寸如图所示(单位:cm).其中主球E(白球或称母球)是指比赛中运动员自始至终用该球击打其它球;目标球F(红球或其它彩色球)是指运动员用主球可以首先直接撞击的球.
如图(2),由于台面上的球①挡住了球路而不能直接用主球E击打目标球F(球①也叫障碍球),此时,需要通过吃库(也叫碰岸)来寻找破障球路.
一次击打主球碰到台边一次叫做吃一库,如图(2)中的球路E→G→F,其中点G是台球碰到台边AB时的反射点;一次击打主球连续碰到台边两次叫做吃两库,如图(3)中的球路E→P→Q→F,其中P、Q分别是台球依次碰到台边AB、BC时的反射点.若主球吃库经过台边反射后碰到目标球,则称吃库破障成功.
【解决问题】
在某场比赛中,某运动员遇到如下情形:主球E、目标球F以及其它三个彩色球①、②和③的位置如图(3)所示,由于障碍球①、②和③的存在,既不能通过左岸(即台边DC)也不能通过右岸(即台边AB)一库解决破障问题,所以运动员打算寻找两库破障球路E→P→Q→F
(如图(3)).
根据上述材料,请你帮助该运动员找出第一次反射点P的位置,即AP的长度为
▲
cm;主球E的两库破障球路E→P→Q→F的路径长EP+PQ+QF=
▲
cm.(注:不考虑台面摩擦作用使球发生旋转以及运动员击球技巧,并将台球看成台面上运动的质点)
三、解答题(第10题14分,第11题16分,共30分)
10.如图,将Rt△DBE的直角顶点B放在x轴的正半轴上,并使得直角边BD所在直线经过点
A(0,1).设原点O关于点B的对称点为,经过点作x轴的垂线交直线BE于点P,设点P的坐标为(x,y).
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)
连结AP,过点作直线l平行于x轴和直线BE相交于点C,求证:.
11.设二次函数的图象与y轴的交点为(0,1),在x轴上截得的线段长为.
(1)
求a、c的值;
(2)
对于任意实数k,规定:当-2≤x≤1时,关于x的函数的最小值称为k的“贡献值”,记作.
求的解析式;
(3)
在(2)条件下,当“贡献值”时,求k的值.
宁波市2016年普通高中保送生考试例卷参考答案及评分标准
(数学)
第Ⅰ部分
数学
一、选择题(本题有5小题,每小题5分,共25分)
题号
1
2
3
4
5
答案
C
A
A
D
B
二、填空题(本题有4小题,每小题5分,共20分)
题号
6
7
8
9
答案
121.75
148.5;
(3分)(2分)
三、解答题(第10题14分,第11题16分,共30分)
10.解:(1),
,
,
∽
,
又点和点关于点对称,点(0,1),
,,,
,得
所求解析式为………………………..(6分)
(2)(方法一):延长交直线于点,则由,直线∥轴知,
是的中位线,
,且,
,
点、、三点共线,
,
又由且知垂直平分,
,,
,,
,
…………………………………(14分)
(方法二):设直线交直线于点D,连结BD,
在△和△中,
≌△(SAS)
,,
又,
,即点、、三点共线,
又由且知垂直平分,
,,
,,
,
.…………………………………(14分)
11.解:(1),
,,
,
化简得
①
又的图象与y轴的交点为(0,1),
②
由①、②得,,…………………………………………..(4分)
(2),,
,
,
对称轴
,对于,分三种情况讨论:
①若,即时,随的增大而增大,
当时,取最小值,
②若,即时,图像过的最低点,
当时,取最小值,
③若,即时,随的增大而减小,
当时,取最小值,.
…………………………….(13分)
(3)①当时,若,得,不合题意,舍去;
②当时,若,得;
③当时,若,得,不合题意,舍去.
综上可知,当时,……………………………….(16分)
(第2题图)
(第5题图)
(第8题图)
(第7题图)
(第9题图)
图(1)
图(2)
图(3)
(备用图)
主球
目标球
(第10题图)
D
(第10题图)
姓名__________就读初中_________________中考报名序号_________________
第Ⅰ部分
数学
一、选择题(本题有5小题,每小题5分,共25分)
1.若,,,则的值为(
)
A.
B.
C.
D.
2.函数的图象如图所示,则函数
的图象与x轴的交点分别是(
)
A.、
B.、
C.、
D.、
3.定义新运算:对于任意实数、都有.若,则关于、的方程组的解是(
)
A.
B.
C.
D.
4.已知函数,当自变量满足时,函数值的取值范围是,
则实数的取值范围是(
)
A.
B.
C.
D.
5.如图,棱长为1的正方体形状的箱子放在地面上(面ABCD着地),先将它绕着棱BC旋转90o,使得面着地;再绕着棱旋转90o,使得面着地;最后绕着棱旋转90o,使得面着地.在这个运动过程中,顶点A在空间所经过的路径长为
(
)
A.
B.
C.
D.
二、填空题(本题有4小题,每小题5分,共20分)
6.已知、、均为实数,且,,则
▲
.
7.如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,
此时,他离地面的高度是
▲
米.
8.如图,一次函数y=x+1的图象交x轴于点E、交反比例函数的图象于点F(点F在第一象限),过线段EF上异于E、F的动点A作x轴的平行线交的图象于点B,过点A、B
作x轴的垂线段,垂足分别是点D、C,则矩形ABCD的面积最大值为
▲
.
9.【阅读材料】
如图(1),长方形ABCD表示落袋台球的球台桌面,其长、宽尺寸如图所示(单位:cm).其中主球E(白球或称母球)是指比赛中运动员自始至终用该球击打其它球;目标球F(红球或其它彩色球)是指运动员用主球可以首先直接撞击的球.
如图(2),由于台面上的球①挡住了球路而不能直接用主球E击打目标球F(球①也叫障碍球),此时,需要通过吃库(也叫碰岸)来寻找破障球路.
一次击打主球碰到台边一次叫做吃一库,如图(2)中的球路E→G→F,其中点G是台球碰到台边AB时的反射点;一次击打主球连续碰到台边两次叫做吃两库,如图(3)中的球路E→P→Q→F,其中P、Q分别是台球依次碰到台边AB、BC时的反射点.若主球吃库经过台边反射后碰到目标球,则称吃库破障成功.
【解决问题】
在某场比赛中,某运动员遇到如下情形:主球E、目标球F以及其它三个彩色球①、②和③的位置如图(3)所示,由于障碍球①、②和③的存在,既不能通过左岸(即台边DC)也不能通过右岸(即台边AB)一库解决破障问题,所以运动员打算寻找两库破障球路E→P→Q→F
(如图(3)).
根据上述材料,请你帮助该运动员找出第一次反射点P的位置,即AP的长度为
▲
cm;主球E的两库破障球路E→P→Q→F的路径长EP+PQ+QF=
▲
cm.(注:不考虑台面摩擦作用使球发生旋转以及运动员击球技巧,并将台球看成台面上运动的质点)
三、解答题(第10题14分,第11题16分,共30分)
10.如图,将Rt△DBE的直角顶点B放在x轴的正半轴上,并使得直角边BD所在直线经过点
A(0,1).设原点O关于点B的对称点为,经过点作x轴的垂线交直线BE于点P,设点P的坐标为(x,y).
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)
连结AP,过点作直线l平行于x轴和直线BE相交于点C,求证:.
11.设二次函数的图象与y轴的交点为(0,1),在x轴上截得的线段长为.
(1)
求a、c的值;
(2)
对于任意实数k,规定:当-2≤x≤1时,关于x的函数的最小值称为k的“贡献值”,记作.
求的解析式;
(3)
在(2)条件下,当“贡献值”时,求k的值.
宁波市2016年普通高中保送生考试例卷参考答案及评分标准
(数学)
第Ⅰ部分
数学
一、选择题(本题有5小题,每小题5分,共25分)
题号
1
2
3
4
5
答案
C
A
A
D
B
二、填空题(本题有4小题,每小题5分,共20分)
题号
6
7
8
9
答案
121.75
148.5;
(3分)(2分)
三、解答题(第10题14分,第11题16分,共30分)
10.解:(1),
,
,
∽
,
又点和点关于点对称,点(0,1),
,,,
,得
所求解析式为………………………..(6分)
(2)(方法一):延长交直线于点,则由,直线∥轴知,
是的中位线,
,且,
,
点、、三点共线,
,
又由且知垂直平分,
,,
,,
,
…………………………………(14分)
(方法二):设直线交直线于点D,连结BD,
在△和△中,
≌△(SAS)
,,
又,
,即点、、三点共线,
又由且知垂直平分,
,,
,,
,
.…………………………………(14分)
11.解:(1),
,,
,
化简得
①
又的图象与y轴的交点为(0,1),
②
由①、②得,,…………………………………………..(4分)
(2),,
,
,
对称轴
,对于,分三种情况讨论:
①若,即时,随的增大而增大,
当时,取最小值,
②若,即时,图像过的最低点,
当时,取最小值,
③若,即时,随的增大而减小,
当时,取最小值,.
…………………………….(13分)
(3)①当时,若,得,不合题意,舍去;
②当时,若,得;
③当时,若,得,不合题意,舍去.
综上可知,当时,……………………………….(16分)
(第2题图)
(第5题图)
(第8题图)
(第7题图)
(第9题图)
图(1)
图(2)
图(3)
(备用图)
主球
目标球
(第10题图)
D
(第10题图)
同课章节目录
