湖南省衡阳县第四中学2016-2017学年高二学业水平第一次模拟考试数学试题 Word版含答案
文档属性
| 名称 | 湖南省衡阳县第四中学2016-2017学年高二学业水平第一次模拟考试数学试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 196.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-07 10:51:06 | ||
图片预览


文档简介
衡阳县四中2017年高中学业水平第一次模拟考试
数 学
本试卷包括选择题、填空题和解答题三部分。
时量120分钟,满分100分。
一、选择题:本大题共10小题,每小题4分,满分40分。在每小题给出的四个选项中,只有一项是符合题目要求的。21世纪教育网版权所有
1.已知集合M={0,1,2},N={x},若M∪N={0,1,2,3},则x的值为( )
A.3 B.2
C.1 D.0
2.如图是一个几何体的三视图,则该几何体为?
A.圆柱 B.圆锥
C.圆台 D.球?
3.在区间内任取一个实数,则此数大于3的概率为
A. B.
C. D.
4.某程序框图如图所示,若输入x的值为1,则输出y的值是
A.2 B.3
C.4 D.5
5.已知向量a=(1,2),b=(x,4),若∥,则实数x的值为( )
A.8 B.2 C.-2 D.-8
6.某学校高一、高二、高三年级的学生人数分别为600,400,800,为了了解教师的教学情况,该校采用分层抽样的方法,从这三个年级中抽取45名学生进行座谈,则高一、高二、高三年级抽取的人数分别为( )21cnjy.com
A.15,5,25 B.15,15,15
C.10,5,30 D.15,10,20
7.如图,在正方体ABCD-A1B1C1D1中,直线
BD与A1C1的位置关系是
A.平行 B.相交
C.异面但不垂直 D.?异面且垂直
8.不等式(x+1)(x-2)≤0的解集为
A.{x|-1≤x≤2} B.?{x|-1<x<2}
C.?{x|x≥2或x≤-1} D.?{x|x>2或x<-1}
9.已知两点P(4,0),Q(0,2),则以线段PQ为直径的圆的方程是( )
A.(x+2)2+(y+1)2=5 B.(x-2)2+(y-1)2=10
C.(x-2)2+(y-1)2=5 D.(x+2)2+(y+1)2=10
10.如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120?,则A、B两点间的距离为( )21·cn·jy·com
A.km B.km
C.1.5km D.2km
二、填空题:本大题共5小题,每小题4分,满分20分.
11.计算:log21+log24=____________。
12.已知1,x,9成等比数列,则实数x=______。
13. 已知点(x,y)在如图所示的平面区域(阴影部分)
内运动,则z=x+y的最大值是____.
14.已知a是函数f(x)=2-log2x的零点,则实数a的值为_____。
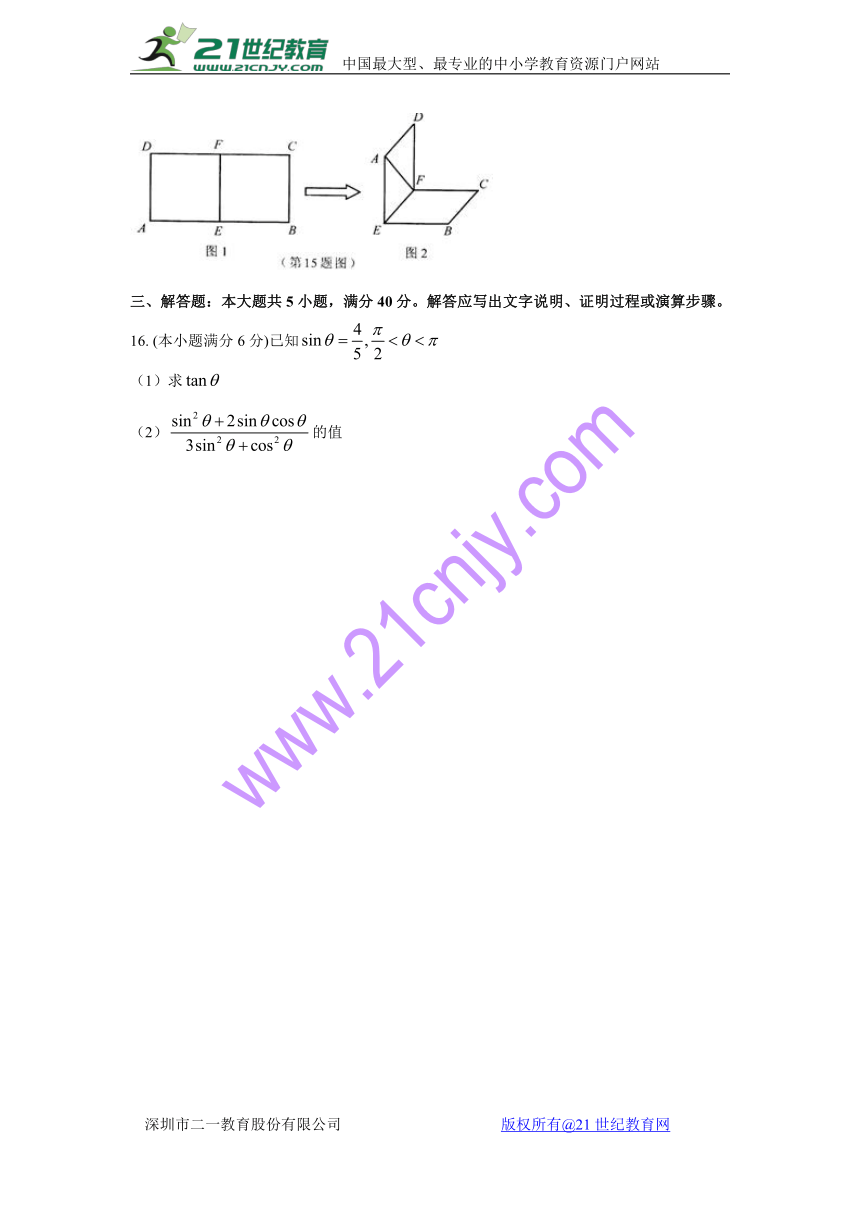
15.如图1,在矩形ABCD中,AB=2BC,E、F分别是AB、CD的中点,现在沿EF把这个矩形折成一个直二面角A-EF-C(如图2),则在图2中直线AF与平面EBCF所成的角的大小www.21-cn-jy.com
为___________。
三、解答题:本大题共5小题,满分40分。解答应写出文字说明、证明过程或演算步骤。
16. (本小题满分6分)已知
(1)求
(2)的值
17.(本小题满分8分)某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如下图所示的频率分布直方图,图中标注的数字模糊不清。21教育网
(1) 试根据频率分布直方图求的值,并估计该公司职员早餐日平均费用的众数;
(2) 已知该公司有1000名职员,试估计该公司有多少职员早餐日平均费用不少于8元?
18.(本小题满分8分)
已知等比数列{an}的公比q=2,且a2,a3+1,a4成等差数列。
(1)求a1及an;
(2)设bn=an+n,求数列{bn}的前5项和S5。
19.已知二次函数满足
(1)求函数解析式
(2)求函数在的最大值和最小值
20.(本小题满分10分)
已知圆C:x2+y2+2x-3=0。
(1)求圆的圆心C的坐标和半径长;
(2)直线l经过坐标原点且不与y轴重合,l与圆C相交于A(x1,y1)、B(x2,y2)两点,求证:为定值;2·1·c·n·j·y
(3)斜率为1的直线m与圆C相交于D、E两点,求直线m的方程,使△CDE的面积最大。
数学试卷参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
B
B
B
D
D
A
C
A
二、填空题 11、2; 12、3;13、5;14、4;15、??(或)
三、解答题
16. 解:(1)
(2)
17、解:(1)高一有(人),高二有(人);
(2)频率为,
人数为(人)。
18.解:(1)由已知得a2=2a1,a3+1=4a1+1,a4=8a1,又2(a3+1)=a2+a4,
所以2(4a1+1)=2a1+8a1,解得a1=1(2分),故an=a1qn-1=2n-1(4分);
(2)因为bn=2n-1+n,所以S5=b1+b2+b3+b4+b5==46(8分)
19. (1);
(2),
∴x=1时,f(x)的最小值为5,x=-2时, f(x)的最大值为14。
20.?解:(1)配方得(x+1)2+y2=4,则圆心C的坐标为(-1,0)(2分),?圆的半径长为2(4分);
(2)设直线l的方程为y=kx,联立方程组
消去y得(1+k2)x2+2x-3=0(5分),则有:(6分)
所以为定值(7分)。
(3)解法一 设直线m的方程为y=kx+b,则圆心C到直线m的距离,
所以(8分),
≤,
当且仅当,即时,△CDE的面积最大(9分)
从而,解之得b=3或b=-1,
故所求直线方程为x-y+3=0或x-y-1=0(10分)
解法二 由(1)知|CD|=|CE|=R=2,
所以≤2,
当且仅当CD⊥CE时,△CDE的面积最大,此时(8分)
设直线m的方程为y=x+b,则圆心C到直线m的距离 (9分)
由,得,
由,得b=3或b=-1,
故所求直线方程为x-y+3=0或x-y-1=0(10分)。
数 学
本试卷包括选择题、填空题和解答题三部分。
时量120分钟,满分100分。
一、选择题:本大题共10小题,每小题4分,满分40分。在每小题给出的四个选项中,只有一项是符合题目要求的。21世纪教育网版权所有
1.已知集合M={0,1,2},N={x},若M∪N={0,1,2,3},则x的值为( )
A.3 B.2
C.1 D.0
2.如图是一个几何体的三视图,则该几何体为?
A.圆柱 B.圆锥
C.圆台 D.球?
3.在区间内任取一个实数,则此数大于3的概率为
A. B.
C. D.
4.某程序框图如图所示,若输入x的值为1,则输出y的值是
A.2 B.3
C.4 D.5
5.已知向量a=(1,2),b=(x,4),若∥,则实数x的值为( )
A.8 B.2 C.-2 D.-8
6.某学校高一、高二、高三年级的学生人数分别为600,400,800,为了了解教师的教学情况,该校采用分层抽样的方法,从这三个年级中抽取45名学生进行座谈,则高一、高二、高三年级抽取的人数分别为( )21cnjy.com
A.15,5,25 B.15,15,15
C.10,5,30 D.15,10,20
7.如图,在正方体ABCD-A1B1C1D1中,直线
BD与A1C1的位置关系是
A.平行 B.相交
C.异面但不垂直 D.?异面且垂直
8.不等式(x+1)(x-2)≤0的解集为
A.{x|-1≤x≤2} B.?{x|-1<x<2}
C.?{x|x≥2或x≤-1} D.?{x|x>2或x<-1}
9.已知两点P(4,0),Q(0,2),则以线段PQ为直径的圆的方程是( )
A.(x+2)2+(y+1)2=5 B.(x-2)2+(y-1)2=10
C.(x-2)2+(y-1)2=5 D.(x+2)2+(y+1)2=10
10.如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120?,则A、B两点间的距离为( )21·cn·jy·com
A.km B.km
C.1.5km D.2km
二、填空题:本大题共5小题,每小题4分,满分20分.
11.计算:log21+log24=____________。
12.已知1,x,9成等比数列,则实数x=______。
13. 已知点(x,y)在如图所示的平面区域(阴影部分)
内运动,则z=x+y的最大值是____.
14.已知a是函数f(x)=2-log2x的零点,则实数a的值为_____。
15.如图1,在矩形ABCD中,AB=2BC,E、F分别是AB、CD的中点,现在沿EF把这个矩形折成一个直二面角A-EF-C(如图2),则在图2中直线AF与平面EBCF所成的角的大小www.21-cn-jy.com
为___________。
三、解答题:本大题共5小题,满分40分。解答应写出文字说明、证明过程或演算步骤。
16. (本小题满分6分)已知
(1)求
(2)的值
17.(本小题满分8分)某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如下图所示的频率分布直方图,图中标注的数字模糊不清。21教育网
(1) 试根据频率分布直方图求的值,并估计该公司职员早餐日平均费用的众数;
(2) 已知该公司有1000名职员,试估计该公司有多少职员早餐日平均费用不少于8元?
18.(本小题满分8分)
已知等比数列{an}的公比q=2,且a2,a3+1,a4成等差数列。
(1)求a1及an;
(2)设bn=an+n,求数列{bn}的前5项和S5。
19.已知二次函数满足
(1)求函数解析式
(2)求函数在的最大值和最小值
20.(本小题满分10分)
已知圆C:x2+y2+2x-3=0。
(1)求圆的圆心C的坐标和半径长;
(2)直线l经过坐标原点且不与y轴重合,l与圆C相交于A(x1,y1)、B(x2,y2)两点,求证:为定值;2·1·c·n·j·y
(3)斜率为1的直线m与圆C相交于D、E两点,求直线m的方程,使△CDE的面积最大。
数学试卷参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
B
B
B
D
D
A
C
A
二、填空题 11、2; 12、3;13、5;14、4;15、??(或)
三、解答题
16. 解:(1)
(2)
17、解:(1)高一有(人),高二有(人);
(2)频率为,
人数为(人)。
18.解:(1)由已知得a2=2a1,a3+1=4a1+1,a4=8a1,又2(a3+1)=a2+a4,
所以2(4a1+1)=2a1+8a1,解得a1=1(2分),故an=a1qn-1=2n-1(4分);
(2)因为bn=2n-1+n,所以S5=b1+b2+b3+b4+b5==46(8分)
19. (1);
(2),
∴x=1时,f(x)的最小值为5,x=-2时, f(x)的最大值为14。
20.?解:(1)配方得(x+1)2+y2=4,则圆心C的坐标为(-1,0)(2分),?圆的半径长为2(4分);
(2)设直线l的方程为y=kx,联立方程组
消去y得(1+k2)x2+2x-3=0(5分),则有:(6分)
所以为定值(7分)。
(3)解法一 设直线m的方程为y=kx+b,则圆心C到直线m的距离,
所以(8分),
≤,
当且仅当,即时,△CDE的面积最大(9分)
从而,解之得b=3或b=-1,
故所求直线方程为x-y+3=0或x-y-1=0(10分)
解法二 由(1)知|CD|=|CE|=R=2,
所以≤2,
当且仅当CD⊥CE时,△CDE的面积最大,此时(8分)
设直线m的方程为y=x+b,则圆心C到直线m的距离 (9分)
由,得,
由,得b=3或b=-1,
故所求直线方程为x-y+3=0或x-y-1=0(10分)。
同课章节目录
