第七章平面直角坐标系 全章导学案
图片预览

文档简介
学校
初中七年级(下)数学
导学案
制作人:
组别:
制作时间:
课题:7.1.1
有序数对
【学习目标】
1、从实际生活中感受有序数对的意义,并会确定平面内物体的位置。
2、通过有序数对确定位置,让学生感受二维空间观,发展符号感及抽象思维能力,让学生体会“具体-抽象-具体”的数学学习过程。
3、培养学生的合作交流意识和探索精神,创造性思维意识。体验数学来源于生活及应用于生活的意识,更好的激发学习兴趣。
【学习重点】理解有序数对的概念,用有序数对来表示位置。
【学习难点】理解有序数对是“有序的”并用它解决实际问题。
【自主学习】
仔细阅读教材第64页第一段和第二段内容并观察教材第64页的插图,说说“7排9号”和“9排7号”的位置有什么区别?
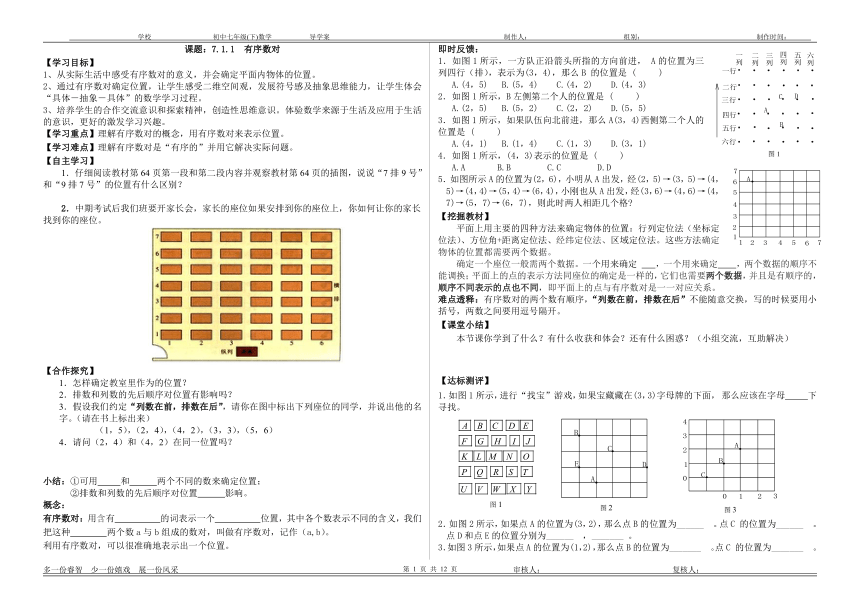
中期考试后我们班要开家长会,家长的座位如果安排到你的座位上,你如何让你的家长找到你的座位。
【合作探究】
怎样确定教室里作为的位置?
排数和列数的先后顺序对位置有影响吗?
假设我们约定“列数在前,排数在后”,请你在图中标出下列座位的同学,并说出他的名字。(请在书上标出来)
(1,5),(2,4),(4,2),(3,3),(5,6)
请问(2,4)和(4,2)在同一位置吗?
小结:①可用
和
两个不同的数来确定位置;
②排数和列数的先后顺序对位置
影响。
概念:
有序数对:用含
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网 )有
的词表示一个
位置,其中各个数表示不同的含义,我们把这种
两个数a与b组成的数对,叫做有序数对,记作(a,b)。
利用有序数对,可以很准确地表示出一个位置。
即时反馈:
1.如图1所示,一方队正沿箭头所指的方向前进,
A的位置为三列四行(排),表示为(3,4),那么B
的位置是
(
)毛
A.(4,5)
B.(5,4)
C.(4,2)
D.(4,3)
2.如图1所示,B左侧第二个人的位置是
(
)
A.(2,5)
B.(5,2)
C.(2,2)
D.(5,5)
3.如图1所示,如果队伍向北前进,那么A(3,4)西侧第二个人的位置是
(
)
A.(4,1)
B.(1,4)
C.(1,3)
D.(3,1)
4.如图1所示,(4,3)表示的位置是
(
)
A.A
B.B
C.C
D.D
5.如图所示A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格
【挖掘教材】
平面上用主要的四种方法来确定物体的位置:行列定位法(坐标定位法)、方位角+距离定位法、经纬定位法、区域定位法。这些方法确定物体的位置都需要两个数据。
确定一个座位一般需两个数据。一个用来确定
,一个用来确定
,两个数据的顺序不能调换;平面上的点的表示方法同座位的确定是一样的,它们也需要两个数据,并且是有顺序的,顺序不同表示的点也不同,即平面上的点与有序数对是一一对应关系。
难点透释:有序数对的两个数有顺序,“列数在前,排数在后”不能随意交换,写的时候要用小括号,两数之间要用逗号隔开。
【课堂小结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?(小组交流,互助解决)
【达标测评】
1.如图1所示,进行“找宝”游戏,如果宝藏藏在(3,3)字母牌的下面,
那么应该在字母
下寻找。
2.如图2所示,如果点A的位置为(3,2),那么点B的位置为______
。点C
的位置为______
。点D和点E的位置分别为______
,_______
。
3.如图3所示,如果点A的位置为(1,2),那么点B的位置为_______
。点C
的位置为_______
。
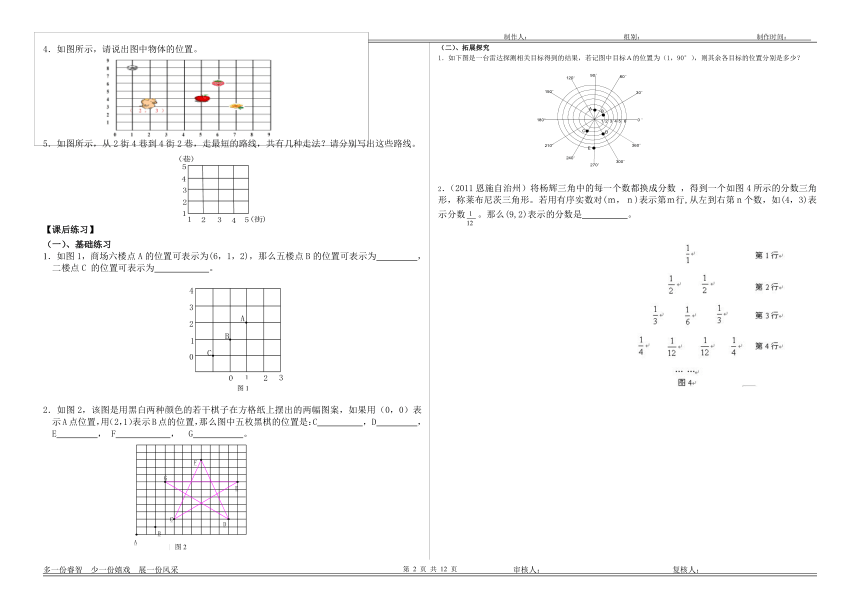
4.如图所示,请说出图中物体的位置。
5.如图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?请分别写出这些路线。
【课后练习】
(一)、基础练习
1.如图1,商场六楼点A的位置可表示为(6,1,2),那么五楼点B的位置可表示为
,二楼点C
的位置可表示为
。
2.如图2,该图是用黑白两种颜色的若干棋子在方格纸上摆出的两幅图案,如果用(0,0)表示A点位置,用(2,1)表示B点的位置,那么图中五枚黑棋的位置是:C
,
D
,
E
,
F
,
G
。
(二)、拓展探究
1.如下图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(1,90°),则其余各目标的位置分别是多少?
2.(2011恩施自治州)将杨辉三角中的每一个数都换成分数
,得到一个如图4所示的分数三角形,称莱布尼茨三角形。若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数。那么(9,2)表示的分数是
。
课题:7.1.2
平面直角坐标系
【学习目标】
1.理解平面直角坐标系,以及横轴、纵轴、原点、坐标等的概念.
2.认识并能画出平面直角坐标系.
3.能在给定直角坐标系中,由点的位置确定点的坐标,由点的坐标确定点的位置.
【学习重点】根据点的坐标在直角坐标系中描出点的位置。
【学习难点】探索特殊的点与坐标之间的关系。
【自主学习】
1、填空:①规定了
、
、
的直线叫做数轴。
②数轴上原点及原点右边的点表示的数是
;原点左边的点表示的数是
。
③画数轴时,一般规定向
(或向
)为正方向。
2、观察:在数轴上,点A的坐标为
,点B的坐标为
。
即:数轴上的点可以用一个
来表示,这个数叫做这个点的
。
反过来,知道数轴上的一个点的坐标,这个点在数轴上的位置也就确定了。
【合作探究】
(一)思考
能不能有一种办法来确定平面内的点的位置呢?
1、平面直角坐标系概念:
平面内画两条互相
、原点
的数轴,组成平面直角坐标系.
水平的数轴称为
或
,习惯上取向
为正方向;
竖直的数轴为
或
,取向
为正方向;
两个坐标轴的交点为平面直角坐标系的
。
2、点的坐标:
我们用一对
表示平面上的点,这对数叫
。表示方法为(a,b).a是点对应
上的数值,b是点在
上对应的数值。
(二)如何在平面直角坐标系中表示一个点
1、以A(2,3)为例,表示方法为:
A点在x轴上的坐标为
,A点在y轴上的坐标为
,
A点在平面直角坐标系中的坐标为(2,3),记作:A(2,3)
2、方法归纳:由点A分别向X轴和
作垂线。
3、强调:X轴上的坐标写在前面。
4、活动:你能说出点B、C、D的坐标吗
注意:横坐标和纵坐标不要写反。
5、思考归纳:原点O的坐标是(
,
),x轴上的点纵坐标都是
,
y轴上的横坐标都是
。横轴上的点坐标为(
,
)
,纵轴上的点坐标为(
,
)
即时反馈:
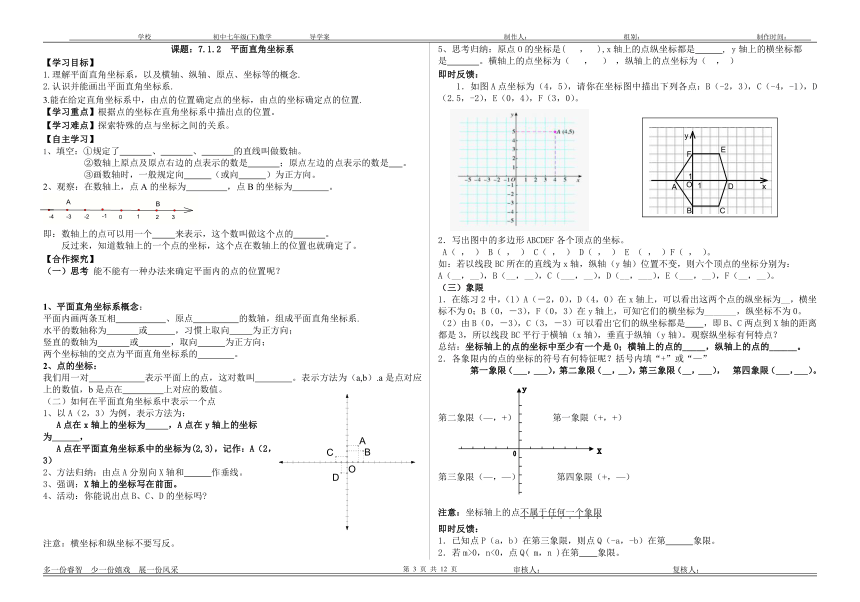
1.如图A点坐标为(4,5),请你在坐标图中描出下列各点:B(-2,3),C(-4,-1),D(2.5,-2),E(0,4),F(3,0)。
写出图中的多边形ABCDEF各个顶点的坐标。
A(
,
)
B(
,
)
C(
,
)
D(
,
)
E
(
,
)F(
,
)。
如:若以线段BC所在的直线为x轴,纵轴(y轴)位置不变,则六个顶点的坐标分别为:
A(__,__),B(__,__),C(___,__),D(__,___),E(___,__),F(__,__)。
(三)象限
1.在练习2中,(1)A(-2,0),D(4,0)在x轴上,可以看出这两个点的纵坐标为__,横坐标不为0;B(0,-3),F(0,3)在y轴上,可知它们的横坐标为_______,纵坐标不为0。
(2)由B(0,-3),C(3,-3)可以看出它们的纵坐标都是
,即B、C两点到X轴的距离都是3,所以线段BC平行于横轴(x轴),垂直于纵轴(y轴)。观察纵坐标有何特点?
总结:坐标轴上的点的坐标中至少有一个是0;横轴上的点的_____,纵轴上的点的______。
2.各象限内的点的坐标的符号有何特征呢?括号内填“+”或“—”
第一象限(
,
),第二象限(
,
),第三象限(
,
),
第四象限(
,
)。
第二象限(—,+)
第一象限(+,+)
第三象限(—,—)
第四象限(+,—)
注意:坐标轴上的点不属于任何一个象限
即时反馈:
1.已知点P(a,b)在第三象限,则点Q(-a,-b)在第
象限。
2.若m>0,n<0,点Q(
m,n
)在第
象限。
【课堂小结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
【达标测评】
(一)、基础练习
1.点A(-2,3)到x轴的距离为
,到y轴的距离是
。
2.x轴上有A、B两点,A点坐标为(3,0),A、B之间的距离为5,则B点坐标为
。
3.若点N(a+5,a-2)在y轴上,则a=
,N点的坐标为
。
4.若点P(a,b)在第四象限内,则a,b的取值范围是(
)
A、a>0,b<0
B、a>0,b>0
C、a<0,b>0
D、a<0,b<0
5.如果点A(x,y)在第三象限,则点B(-x,y-1)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.点P在y轴左方、x轴上方,距y轴、x轴分别为3、4个单位长度,点P的坐标是(
)
A.(3,-4)
B.(-3,4)
C.(4,-3)
D.(-4,3)
7.已知点P(x,y)在第二象限,且,则点P的坐标为(
)
A.(-2,3)
B.(2,-3)
C.(-3,2)
D.(2,3)
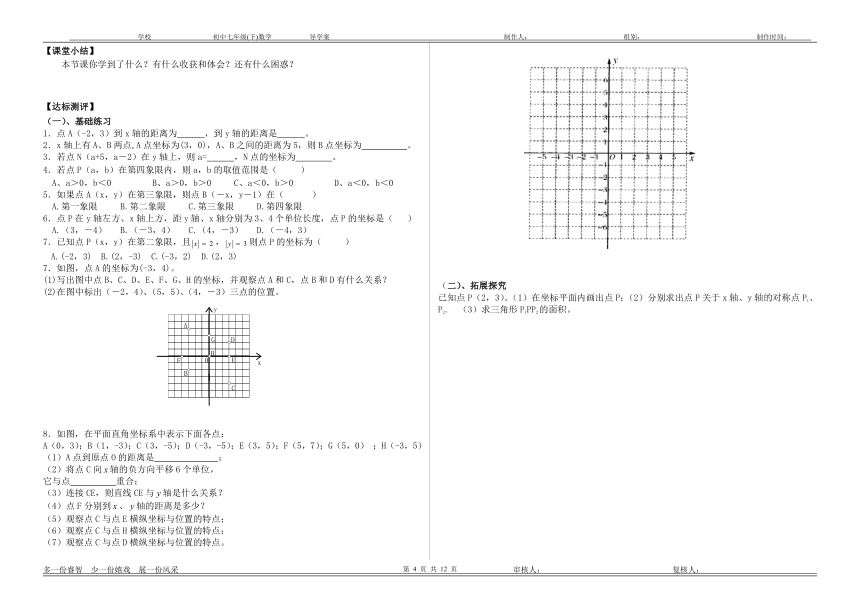
7.如图,点A的坐标为(-3,4)。
(1)写出图中点B、C、D、E、F、G、H的坐标,并观察点A和C,点B和D有什么关系?
(2)在图中标出(-2,4)、(5,5)、(4,-3)三点的位置。
如图,在平面直角坐标系中表示下面各点:
A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0)
;H(-3,5)
(1)A点到原点O的距离是
;
(2)将点C向轴的负方向平移6个单位,
它与点
重合;
(3)连接CE,则直线CE与轴是什么关系?
(4)点F分别到、轴的距离是多少?
(5)观察点C与点E横纵坐标与位置的特点;
(6)观察点C与点H横纵坐标与位置的特点;
(7)观察点C与点D横纵坐标与位置的特点。
(二)、拓展探究
已知点P(2,3)。(1)在坐标平面内画出点P;(2)分别求出点P关于x轴、y轴的对称点P1、P2. (3)求三角形P1PP2的面积。
课题:7.1.3
平面直角坐标系习题课
【学习目标】
.加深对平面直角坐标系认识,熟悉用坐标表示点,能准确描出点的位置。
【学法指导】
由两条相互垂直、原点重合的数轴建立了平面直角坐标系。坐标平面内点与坐标的对应关系,顺利地实现由一维到二维的过渡,即由数字体现了点的位置,由点的位置体现了一种图形形状及大小,由抽象到具体。
【学习重点】进一步理解平面直角坐标系的相关概念及性质。
【自主学习】
1.平面直角坐标系的概念:平面内两条互相
、
重合的
组成的图形。其中,水平的数轴称为
或
,习惯上取向
为正方向;竖直的数轴称为
或
,习惯上取向
为方正向。两坐标轴的交点为平面直角坐标系的
,记为O,其坐标为
。有了平面直角坐标系,平面内的点就可以用一个
来表示,叫做点的坐标。建立平面直角坐标系后,平面被坐标轴分成四部分,分别叫
,
,
,
。坐标轴上的点不属于
。平面直角坐标系内一点A的坐标用(a,b)来表示,a是
坐标、b是
坐标这里的两个数据,一个表示水平方向与A点的距离,另一个表示竖直方向上到A点的距离。
2.各象限点的坐标的特点是:
⑴点P(x,y)在第一象限,则x
0,y
0.⑵点P(x,y)在第二象限,则x
0,y
0.
⑶点P(x,y)在第三象限,则x
0,y
0.⑷点P(x,y)在第四象限,则x
0,y
0。
3.坐标轴上点的坐标的特点是:
⑴点P(x,y)在x轴上,则x
,y
.
⑵点P(x,y)在y轴上,则x
,y
。
【合作探究一】
全班同学坐位均匀分布,不留走廊。以班内最中间的一个学生为原点,以这个学生所在的这一排为X轴,以这个学生所在列为Y轴,建立直角坐标系,由教师指定,并回答下列问题。
1、请在一、二、三、四象限内同学分别站起来,说出各自的坐标。
2、请在坐标上的同学分别站起来,并说出两轴上的点的坐标的特征;
X轴上的点:
Y轴上的点:
3、任选一行,那些同学所在直线与两轴平行(垂直),并说出该直线上的点的坐标特征。
(1)与X轴平行的点:
(2)与Y轴平行的点:
4、请每位同学找出你关于X(Y、原点)对称的同学,并说出关于两轴及原点的对称点的坐标特征:
(1)关于X轴的对称点:
(2)关于Y轴的对称点:
(3)关于原点的对称点:
5、请在坐标系的角平分线上的同学,并说出各自的特征:
(1)一、二象限的角平分线上:
(2)三、四象限的角平分线上:
【合作探究二】
探索:你知道下面两点和连线与坐标轴的关系吗?画一画,找一找。
⑴当≠0时,线段
y轴。
即当两个点的横坐标相同时,这两个点的连线
y轴。
⑵当≠0时,线段
x轴。
即当两个点的纵坐标相同时,这两个点的连线
x轴。
即时反馈:
1.已知坐标平面内点M(a,b)在第三象限,那么点N(b,-a)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知点A(2,-3),线段AB与坐标轴没有交点,则点B的坐标可能是
(
)
A.(-1,-2)
B.(
3,-2)
C.(1,2)
D.(-2,3)
3.点P(m+3,
m+1)在直角坐标系的x轴上,则点P坐标为(
)
A.(0,-2)
B.(
2,0)
C.(
4,0)
D.(0,-4)
4.已知点A(2,-3),线段AB与坐标轴平行,则点B的坐标可能是
(
)
A.(-1,-2)
B.(
3,-2)
C.(1,2)
D.(-2,-3)
5.如图,在直角坐标系中,,,.
求:的面积。
【课堂小结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
【达标测评】
1.若点P(2,k-1)在第一象限,则k
的取值范围是_______。
2.点P(m2-1,
m+3)在直角坐标系的y轴上,则点P坐标为
。
3.已知AB∥x轴,A点的坐标为(3,2),且AB=4,则B点的坐标为
。
4.已知点P(x,
|x|),则点P一定(
)
A.在第一象限
B.在第一或第四象限
C.在x轴上方
D.不在x轴下方
5.若点P(x,y)的坐标满足xy=0(x≠y),则点P在(
)
A.原点上
B.x轴上
C.y轴上
D.x轴上或y轴上
6.点E与点F的纵坐标相同,横坐标不同,则直线EF与y轴的关系是(
)
A.相交
B.垂直
C.平行
D.以上都不正确
7.建立适当的平面直角坐标系,表示边长为4的正方形各点的坐标。
8.如图,将边长为1的正三角形沿轴正方向连续翻转2008次,点在X轴上依次落在点,……,的位置,求点,的坐标.
【课后练习】
(一)、基础练习
1.若点A的坐标是(-3,5),则它到x轴的距离是
,到y轴的距离是
。
2.点B在x轴下方,y轴右侧,距y轴、x轴分别是2、4个单位长度,点B的坐标是
。
3.点P(a-1,a
2-9)在x轴负半轴上,则P点坐标是 。
4.
在平面直角坐标系中,适合条件∣x∣=6,
∣x-y∣=8的点p(x,y)的个数是(
)
A.2
B.3
C.4
D.5
5.已知点P(a,b),ab>0,a+b<0,则点P在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.在平面直角坐标系中,若A(-2,3),B(2,-3),则点A与点B(
)
A.关于x轴对称
B.
关于y轴对称
C.
关于原点对称
D.以上都不对
7、在直角坐标系中有两个点C、D,且CD⊥X轴,那么C、D两点的横坐标(
)
A、不相等
B、互为相反数
C、相等
D、相等或互为相反数
8、已知P(-2,3)则P点关于X轴的对称点P1的坐标为
,P点关于一、三象限的角平分线上的对称点P2的坐标为
。
(二)、拓展探究
1、画出以A(0,0)
,B(5,0)
,
C(6,4),
D(1,4)
为顶点的四边形ABCD,并求其面积。
2、如图,已知:A(3,2),B(5,0),E(4,1),求△AOE的面积。
3、在平面直角坐标系中,点A(0,3),B(0,-2),点C在x轴上,如果△ABC的面积是15,求点C的坐标。
课题:7.2.1
用坐标表示地理位置
【学习目标】
1、了解用平面直角坐标系来表示地理位置的意义及主要过程,能用坐标系来描述地理位置。
2、通过学习用坐标表示地理位置,培养解决实际问题的能力,发展空间观念。
【学习重点】利用坐标表示地理位置。
【学习难点】建立适当的坐标系表示地理位置。
【自主学习】
1.如图(图1),这是某市部分简图。
(1)请以火车站为坐标原点建立平面直角坐标系,并分别写出各地的坐标。
(2)改变坐标原点,重新建立一个平面直角坐标系,并写出各地坐标。
(图1)
(图2)
4.不管是出差办事,还是出去旅游,人们都愿意带上一幅地图,它给人们出行带来了很大方便.如(图2):这是北京市地图的一部分,你知道怎样用坐标表示地理位置吗?
【合作探究】
(一)探究用坐标表示地理位置的方法
1.根据以下条件画一幅示意图,标出学校和小刚家、小强家、小敏家的位置.
小刚家:出校门向东走1500
m,再向北走2000
m.
小强家:出校门向西走2000
m,再向北走3500
m,最后再向东走500
m.
小敏家:出校门向南走1000
m,再向东走3000
m,最后向南走750
m.
问题1:如何建立平面直角坐标系呢?以何参照点为原点?如何确定x轴、y轴?怎样确定单位长度呢?
解:如(图3):以
为坐标原点,以正东、正北方向为
轴、
轴正方向建立直角坐标系,取一个单位长度代表
米,则小刚家(
,
),小强家(
,
)小敏家(
,
)。
(图3)
(图4)
问题2:选取学校所在位置为原点,并以正东、正北方向为x轴、y轴的正方向有什么优点?
小结:利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程如下:
(1)建立坐标系,选择一个____________为原点,确定x轴、y轴的___方向;
(2)根据具体问题确定______________;
(3)在坐标平面内画出这些点,写出各点的_______和各个地点的名称.
即时反馈:
根据以下条件画一幅示意图,标出某一公园的各个景点.【请在(图4)上完成】
菊花园:从中心广场向北走150米,再向东走150米;
湖心亭:从中心广场向西走150米,再向北走100米;
松风亭:从中心广场向西走100米,再向南走50米;
育德泉:从中心广场向北走200米.
(二)探究表示地理位置的其他方法
即时反馈:
教材第75页:练习
第2题
【反思总结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?(小组交流,互助解决)
【达标测评】
1.如图,若在象棋盘上建立直角坐标系,使帅位于点(-1,-2).馬位于点(2,-2),则兵位于点
2.以百色汽车总站为坐标原点,向阳路为y轴建立直角坐标系,百色起义纪念馆位置如图所示,则其所覆盖的坐标可能是( )
A、(-5,3)B、(4,3)C、(5,-3)D、(-5,-3)
3.以下是甲、乙、丙三人看地图时对四个地标的描述:
甲:从学校向北直走500公尺,再向东直走100公尺可到图书馆.
乙:从学校向西直走300公尺,再向北直走200公尺可到邮局.
丙:邮局在火车站西方200公尺处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站( )
A、向南直走300公尺,再向西直走200公尺
B、向南直走300公尺,再向西直走600公尺
C、向南直走700公尺,再向西直走200公尺
D、向南直走700公尺,再向西直走600公尺
4.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是
5.王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,-2),你能帮她求出其他各景点的坐标吗?
【课后练习】
(一)、基础练习
1.利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程为:
⑴建立坐标系,选择一个适当的______为原点,确定x轴、y轴的_______;
⑵确定适当的_______,在坐标轴上标出单位长度;
⑶在坐标平面内画出这些点,写出各点的_______和各个地点的________。
2.图是某乡镇的示意图(图中每个小正方形的边长均为个单位长度)。
⑴试建立直角坐标系,用坐标表示各地的位置:
⑵如果已知王马村的坐标是(0,0),请用坐标表示出大山镇、爱心中学的位置。
⑶如果已知映月湖的坐标是(6,-3),请用坐标表示出大山镇、红旗乡的位置。
(二)、拓展探究
张先生手中有一张残缺不全的旧地图,依稀可见钟楼坐标A(4,-2),街口坐标B(4,2),资料记载张先生祖居坐标C(1,-2)。你能帮张先生找到他家的老屋吗?
课题:7.2.2
用坐标表示平移
【学习目标】
1.掌握坐标变化与图形平移的关系;能利用点的平移规律将平面图形进行平移;会根据图形上点的坐标的变化,来判定图形的移动过程.
2.
培养探究的兴趣和归纳概括的能力,发展学生的形象思维能力,和数形结合的意识.
【学习重点】掌握坐标变化与图形平移的关系;
【学习难点】利用坐标变化与图形平移的关系解决实际问题。
【自主学习】
问题:请同学们回忆前面我们学移知识,什么叫平移?图形的平移有哪些性质?
【合作探究一】
画图观察:在图中描出点A(-2,-3)作以下平移,请在图上标出平移后的点并写它们的坐标。
A(-2,-3)向右平移5个单位得到A2(
,
)
A(-2,-3)向左平移3个单位得到A3(
,
)
A(-2,-3)向右平移5个单位得到A4(
,
)
A(-2,-3)向右平移5个单位得到A5(
,
)
观察平移前后点的坐标的变化,你能从中发现什么规律?归纳“图形平移与点的坐标变化”之间的关系
(1)左、右平移:
原图形上的点(x,y)
(
)
原图形上的点(x,y)
(
)
(2)上、下平移:
原图形上的点(x,y)
(
)
原图形上的点(x,y)
(
)
即时反馈:
1.在平面直角坐标系中,有一点P(-4,2),若将点P:
(1)向左平移2个单位长度,所得点的坐标为_____________;
(2)向右平移3个单位长度,所得点的坐标为_____________;
(3)向下平移4个单位长度,所得点的坐标为_____________;
(4)向上平移5个单位长度,所得点的坐标为_____________;
2.已知A(1,4),B(-4,0),C(2,0)。
⑴将△ABC向左平移三个单位后,点A、B、C的坐标
分别变为
,
,
。
⑵将△ABC向下平移三个单位后,点A、B、C的坐标
分别变为
,
,
。
3、思考并归纳“点的坐标变化与图形平移”之间的关系
(1)横坐标变化,纵坐标不变:
原图形上的点(x,y)
向
平移
个单位
原图形上的点(x,y)
向
平移
个单位
(2)横坐标不变,纵坐标变化:
原图形上的点(x,y)
向
平移
个单位
原图形上的点(x,y)
向
平移
个单位
即时反馈:
1.已知A(1,4),B(-4,0),C(2,0)。
⑴将△ABC三顶点A、B、C的横坐标都增加2,相应的新图形就是把原图形向
平移了
个单位长度。
⑵将△ABC三顶点A、B、C的纵坐标都增加3,相应的新图形就是把原图形向
平移了
个单位长度。
⑶将△ABC三顶点A、B、C的横坐标都减少3,纵坐标都减少4相应的新图形就是把原图形先向
平移了
个单位长度,再向
平移了
个单位长度。
2.如图,三角形ABC中任意一点经平移后对应点为,将三角形ABC作同样的平移得到三角形.画出三角形,并写出三个顶点的坐标.
【合作探究二】
1、做一做,如图
(1)请写出点A的坐标;
(2)分别作出点A关于x轴、y轴的对称点,并写出它们的坐标,记为A2,A3;
(3)观察一下,点A与A2,点A与A3的坐标,有什么特别之处吗,你有什么发现呢?(哪些变了,哪些没变?)
观察点A2和点的位置,它们可看作关于哪个点对称?它们的坐标有什么关系?
归纳:A
A2(关于x轴对称),
不变,纵坐标
。
A
A3
(关于y轴对称)纵坐标
,
互为相反数。
(5)如果改变点A的坐标,这个规律仍然成立吗?你能否用字母来表示一下这个规律呢?
在直角坐标系中,点(a,b)关于x轴的对称点的坐标为
,关于y轴的对称点的坐标为
。
【课堂小结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
【达标测评】
1、能完成坐标平面内的点的平移时,坐标是如何变化的吗?填写下图(h>0):
(a,
)
向上平移h个单位
向左平移h个单位
向右平移h个单位
(
,b)
(a,b)
(
,b)
向下平移h个单位
(a,
)
难点透释:图形平移与坐标变化的关系
图像左右平移,纵坐标不变,横坐标左(移)减右(移)加;
图像上下平移,横坐标不变,纵坐标下(移)减上(移)加。
2、已知点M(-4,2),将点先向下平移3个单位长度,再向左平移3个单位长度,则点M在坐标系内的坐标为
.
3、平面直角坐标系中△ABC三个顶点的横坐标保持不变,
纵坐标都减去了3,则得到的新三角形与原三角形相比向
平移了
个单位。
4、在平面直角坐标系中,将点(2,1)向右平移3个单位长度,可以得到对应点坐标
;将点(2,-1)向左平移3个单位长度可得到对应点坐标
;
将点(2,5)向上平移3单位长度可得对应点坐标
;将点(-2,5)向下平移3单位长度可得对应点坐标
。
5、线段AB两端点坐标分别为A(-1,4),B(-4,1),现将它向左平移4个单位长度,得到线段A1B1,则A1、B1的坐标依次分别为(
)
A.(-5,0),(-8,-3)
B.(3,7),(0,5)
C.(-5,4),(-8,1)
D.(3,4),(0,1)
6、坐标系中,将正方形向上平移3个单位后,得到的正方形各顶点与原正方形各顶点坐标相比(
)
A.横坐标不变,纵坐标加3
B.纵坐标不变,横坐标加3
C.横坐标不变,纵坐标乘以3
D.纵坐标不变,横坐标乘以3
7、如图,小鱼的“嘴巴”所在的坐标是(1,1),请画出图形并回答下列问题。
⑴小鱼沿x轴向左平移6个单位,此时小鱼的“嘴巴”所在的坐标是多少?
⑵小鱼沿y轴向下平移4个单位,此时小鱼的“嘴巴”所在的坐标是多少?
8、将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1,
画出图形并写出点A1、B1、C1的坐标。
9、在平面直角坐标系中,将坐标(0,0),(2,4),(4,4),(2,0)的点用线段依次连接起来形成一个图案:
⑴这四个点的纵坐标若保持不变,横坐标变成原来的一半,将所得的四个点用线段依次连接起来,所得的图案与原图案相比有什么变化?请在平面直角坐标系中画出图形。
⑵纵坐标保持不变,横坐标分别加1呢?
课题:平面直角坐标系全章复习
一、本章知识结构图
二、本章知识梳理
1.有序数对:用含有
的词表示一个确定的位置,其中各个数表示
的含义,我们把这种有
的
个数a与b组成的数对,叫做有序数对,记作
。
2.平面直角坐标系的概念:平面内两条互相
、
重合的
组成的图形。
3.各象限点的坐标的特点是:
⑴点P(x,y)在第一象限,则x
0,y
0.⑵点P(x,y)在第二象限,则x
0,y
0.
⑶点P(x,y)在第三象限,则x
0,y
0.⑷点P(x,y)在第四象限,则x
0,y
0。
4.坐标轴上点的坐标的特点是:
⑴点P(x,y)在x轴上,则x
,y
.⑵点P(x,y)在y轴上,则x
,y
。
5.比例尺是图距与
的比。
6.利用平面直角坐标系来表示地理位置的一般步骤是:
⑴建立坐标系,选择一个适当的参照点为____,确定X轴、Y轴的______。
⑵根据具体问题确定适当的_______,在坐标轴上标出_______。
⑶在坐标平面内画出这些点,写出各点的______和各个地点的名称。
7.图形平移与点的坐标变化之间的关系(其中a、b为正数)
(1)左、右平移:
原图形上的点(x,y)
(
)
原图形上的点(x,y)
(
)
(2)上、下平移:
原图形上的点(x,y)
(
)
原图形上的点(x,y)
(
)
8.点的坐标变化与图形平移之间的关系(其中a、b为正数)
(1)横坐标变化,纵坐标不变:
原图形上的点(x,y)
向
平移
个单位
原图形上的点(x,y)
向
平移
个单位
(2)横坐标不变,纵坐标变化:
原图形上的点(x,y)
向
平移
个单位
原图形上的点(x,y)
向
平移
个单位
9.一、三象限的角平分线上的点:x=y;二、四象限的角平分线上的点:
平行于x轴的直线上的点
相等,平行于y轴的直线上的点
相等。
点P(x,y)
关于x轴的对称点
;关于y轴的对称点
。
关于原点的对称点
距离计算:
点P(a,b)到x轴的距离为_____,到y轴的距离为_____,到原点的距离为_____。
A(a,0),B(c,0)间的距离=____;A(0,b),B(0,d)间的距离=______;
A(a,0),B(0,d)
间的距离=________;A(a,b),B(c,d)间的距离=______。
三、巩固练习
1.将点P(-2,3)向右平移3个单位,再向下平移5
个单位,所得的点的坐标为
。
2.点P到x轴、y轴的距离分别是2、1,则点P的坐标可能为
。
3.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的坐标是
。
4.点P(x,y)满足xy>0,则点P在(
)
A.第一象限
B.
第二象限
C.
第三象限
D.
第一象限和第三象限
5.已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为(
)
A.3
B.1
C.0
D.-1
6.平面内点的坐标是(
)
A.一个点
B.一个图形
C.一个数
D.一个有序数对
7.在平面直角坐标系内,下列说法错误的是(
)
A.原点O不在任何象限内
B.原点O的坐标是0
C.原点O既在X轴上也在Y轴上
D.原点O在坐标平面内
8.X轴上的点P到Y轴的距离为2,则点P的坐标为(
)
A.(2,0)
B.(-2,0)
C.(0,2)
D.(2,0)或(-2,0)
9.三角形ABC三个顶点的坐标分别是
A(4,3)B(3,1)C(1,2),请你在平面直角坐标系中描出这个三角形,然后先将其向左平移4个单位,再将其向下平移2个单位,画出平移后的图形并写出相应顶点的坐标。
10.如图,写出三角形ABC各顶点的坐标并且求出三角形的面积。
四、课后练习
(一)、基础练习
1.有序数对(3,2)表示第3列第2排的座位,则位于第5列第4排的座位应记作(
)
A.(4,5)
B.(5,4)
C.(5、4)
D.(4、5)
2.在平面直角坐标系中,对于坐标P(2,5),下列说法错误的是(
)
A.P(2,5)表示这个点在平面内的位置
B.点P的纵坐标是5
C.它与点(5,2)表示同一个坐标
D.点P到x轴的距离是5
3.在平面直角坐标系中,点C(-2,4)向右平移3个单位后得到D点,则D点的坐标是(
)
A.(1,4)
B.(-5,4)
C.(-2,7)
D.(-2,1)
4.下列坐标所表示的点中,距离坐标系的原点最近的是
(
)
A.(-1,1)
B.(2,1)
C.(0,2)
D.(0,-2)
5.在平面直角坐标系中,若以点A(0,-3)为圆心,5为半径画一个圆,则这个圆与y轴的负半轴相交的点坐标是(
)
A.(8,0)
B.(
0,-8)
C.(0,8)
D.(-8,0)
6.已知x轴上的点P到y
轴的距离是3,则点P坐标是________
_。
7.已知点A(2,-3),若将点A向左平移3个单位得到点B,则点B坐标是_____
_,若将点A向上平移4个单位得到点C,则点C坐标是____
__。
在坐标轴上与点M(3,-4)距离等于5的点,共有几个?并求出这几个坐标
9.平面内有A、B、C、D、E共5个点。
⑴请建立适当的平面直角坐标系,写出A、B、C、D、E的坐标;
⑵以线段AB为一边,画出一个平行四边形。
10.现有一张利用平面直角坐标系画出来的某公园景区地图,如图,若知道游乐园D的坐标为(2,-2)。
⑴请按题意建立平面直角坐标系,写出其他景点的坐标;
⑵请指出距离原点最近和最远的景点。
二、拓展探究
如图,是两个五子棋爱好者对弈图(甲执黑子先行,乙执白子后走),观察棋盘,若点M的位置记作(3,D),
乙必须在哪个位置上落子,才不会让甲在短时间内获胜?为什么?
图1
图3
图2
图1
图1
_
B
_
A
_
C
_
D
_
E
_
G
_
F
图(2)
图2
B
A
北
60°
救生船
遇险船
·A
·B
向右平移a个单位
向左平移a个单位
向上平移b个单位
向下平移b个单位
(x+a,y)
(x-a,y)
(x,y+b)
(x,y-b)
向右平移a个单位
向左平移a个单位
向上平移b个单位
向下平移b个单位
(x+a,y)
(x-a,y)
(x,y+b)
(x,y-b)
M
多一份睿智
少一份嬉戏
展一份风采
审核人:
复核人:
初中七年级(下)数学
导学案
制作人:
组别:
制作时间:
课题:7.1.1
有序数对
【学习目标】
1、从实际生活中感受有序数对的意义,并会确定平面内物体的位置。
2、通过有序数对确定位置,让学生感受二维空间观,发展符号感及抽象思维能力,让学生体会“具体-抽象-具体”的数学学习过程。
3、培养学生的合作交流意识和探索精神,创造性思维意识。体验数学来源于生活及应用于生活的意识,更好的激发学习兴趣。
【学习重点】理解有序数对的概念,用有序数对来表示位置。
【学习难点】理解有序数对是“有序的”并用它解决实际问题。
【自主学习】
仔细阅读教材第64页第一段和第二段内容并观察教材第64页的插图,说说“7排9号”和“9排7号”的位置有什么区别?
中期考试后我们班要开家长会,家长的座位如果安排到你的座位上,你如何让你的家长找到你的座位。
【合作探究】
怎样确定教室里作为的位置?
排数和列数的先后顺序对位置有影响吗?
假设我们约定“列数在前,排数在后”,请你在图中标出下列座位的同学,并说出他的名字。(请在书上标出来)
(1,5),(2,4),(4,2),(3,3),(5,6)
请问(2,4)和(4,2)在同一位置吗?
小结:①可用
和
两个不同的数来确定位置;
②排数和列数的先后顺序对位置
影响。
概念:
有序数对:用含
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网 )有
的词表示一个
位置,其中各个数表示不同的含义,我们把这种
两个数a与b组成的数对,叫做有序数对,记作(a,b)。
利用有序数对,可以很准确地表示出一个位置。
即时反馈:
1.如图1所示,一方队正沿箭头所指的方向前进,
A的位置为三列四行(排),表示为(3,4),那么B
的位置是
(
)毛
A.(4,5)
B.(5,4)
C.(4,2)
D.(4,3)
2.如图1所示,B左侧第二个人的位置是
(
)
A.(2,5)
B.(5,2)
C.(2,2)
D.(5,5)
3.如图1所示,如果队伍向北前进,那么A(3,4)西侧第二个人的位置是
(
)
A.(4,1)
B.(1,4)
C.(1,3)
D.(3,1)
4.如图1所示,(4,3)表示的位置是
(
)
A.A
B.B
C.C
D.D
5.如图所示A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格
【挖掘教材】
平面上用主要的四种方法来确定物体的位置:行列定位法(坐标定位法)、方位角+距离定位法、经纬定位法、区域定位法。这些方法确定物体的位置都需要两个数据。
确定一个座位一般需两个数据。一个用来确定
,一个用来确定
,两个数据的顺序不能调换;平面上的点的表示方法同座位的确定是一样的,它们也需要两个数据,并且是有顺序的,顺序不同表示的点也不同,即平面上的点与有序数对是一一对应关系。
难点透释:有序数对的两个数有顺序,“列数在前,排数在后”不能随意交换,写的时候要用小括号,两数之间要用逗号隔开。
【课堂小结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?(小组交流,互助解决)
【达标测评】
1.如图1所示,进行“找宝”游戏,如果宝藏藏在(3,3)字母牌的下面,
那么应该在字母
下寻找。
2.如图2所示,如果点A的位置为(3,2),那么点B的位置为______
。点C
的位置为______
。点D和点E的位置分别为______
,_______
。
3.如图3所示,如果点A的位置为(1,2),那么点B的位置为_______
。点C
的位置为_______
。
4.如图所示,请说出图中物体的位置。
5.如图所示,从2街4巷到4街2巷,走最短的路线,共有几种走法?请分别写出这些路线。
【课后练习】
(一)、基础练习
1.如图1,商场六楼点A的位置可表示为(6,1,2),那么五楼点B的位置可表示为
,二楼点C
的位置可表示为
。
2.如图2,该图是用黑白两种颜色的若干棋子在方格纸上摆出的两幅图案,如果用(0,0)表示A点位置,用(2,1)表示B点的位置,那么图中五枚黑棋的位置是:C
,
D
,
E
,
F
,
G
。
(二)、拓展探究
1.如下图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(1,90°),则其余各目标的位置分别是多少?
2.(2011恩施自治州)将杨辉三角中的每一个数都换成分数
,得到一个如图4所示的分数三角形,称莱布尼茨三角形。若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数。那么(9,2)表示的分数是
。
课题:7.1.2
平面直角坐标系
【学习目标】
1.理解平面直角坐标系,以及横轴、纵轴、原点、坐标等的概念.
2.认识并能画出平面直角坐标系.
3.能在给定直角坐标系中,由点的位置确定点的坐标,由点的坐标确定点的位置.
【学习重点】根据点的坐标在直角坐标系中描出点的位置。
【学习难点】探索特殊的点与坐标之间的关系。
【自主学习】
1、填空:①规定了
、
、
的直线叫做数轴。
②数轴上原点及原点右边的点表示的数是
;原点左边的点表示的数是
。
③画数轴时,一般规定向
(或向
)为正方向。
2、观察:在数轴上,点A的坐标为
,点B的坐标为
。
即:数轴上的点可以用一个
来表示,这个数叫做这个点的
。
反过来,知道数轴上的一个点的坐标,这个点在数轴上的位置也就确定了。
【合作探究】
(一)思考
能不能有一种办法来确定平面内的点的位置呢?
1、平面直角坐标系概念:
平面内画两条互相
、原点
的数轴,组成平面直角坐标系.
水平的数轴称为
或
,习惯上取向
为正方向;
竖直的数轴为
或
,取向
为正方向;
两个坐标轴的交点为平面直角坐标系的
。
2、点的坐标:
我们用一对
表示平面上的点,这对数叫
。表示方法为(a,b).a是点对应
上的数值,b是点在
上对应的数值。
(二)如何在平面直角坐标系中表示一个点
1、以A(2,3)为例,表示方法为:
A点在x轴上的坐标为
,A点在y轴上的坐标为
,
A点在平面直角坐标系中的坐标为(2,3),记作:A(2,3)
2、方法归纳:由点A分别向X轴和
作垂线。
3、强调:X轴上的坐标写在前面。
4、活动:你能说出点B、C、D的坐标吗
注意:横坐标和纵坐标不要写反。
5、思考归纳:原点O的坐标是(
,
),x轴上的点纵坐标都是
,
y轴上的横坐标都是
。横轴上的点坐标为(
,
)
,纵轴上的点坐标为(
,
)
即时反馈:
1.如图A点坐标为(4,5),请你在坐标图中描出下列各点:B(-2,3),C(-4,-1),D(2.5,-2),E(0,4),F(3,0)。
写出图中的多边形ABCDEF各个顶点的坐标。
A(
,
)
B(
,
)
C(
,
)
D(
,
)
E
(
,
)F(
,
)。
如:若以线段BC所在的直线为x轴,纵轴(y轴)位置不变,则六个顶点的坐标分别为:
A(__,__),B(__,__),C(___,__),D(__,___),E(___,__),F(__,__)。
(三)象限
1.在练习2中,(1)A(-2,0),D(4,0)在x轴上,可以看出这两个点的纵坐标为__,横坐标不为0;B(0,-3),F(0,3)在y轴上,可知它们的横坐标为_______,纵坐标不为0。
(2)由B(0,-3),C(3,-3)可以看出它们的纵坐标都是
,即B、C两点到X轴的距离都是3,所以线段BC平行于横轴(x轴),垂直于纵轴(y轴)。观察纵坐标有何特点?
总结:坐标轴上的点的坐标中至少有一个是0;横轴上的点的_____,纵轴上的点的______。
2.各象限内的点的坐标的符号有何特征呢?括号内填“+”或“—”
第一象限(
,
),第二象限(
,
),第三象限(
,
),
第四象限(
,
)。
第二象限(—,+)
第一象限(+,+)
第三象限(—,—)
第四象限(+,—)
注意:坐标轴上的点不属于任何一个象限
即时反馈:
1.已知点P(a,b)在第三象限,则点Q(-a,-b)在第
象限。
2.若m>0,n<0,点Q(
m,n
)在第
象限。
【课堂小结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
【达标测评】
(一)、基础练习
1.点A(-2,3)到x轴的距离为
,到y轴的距离是
。
2.x轴上有A、B两点,A点坐标为(3,0),A、B之间的距离为5,则B点坐标为
。
3.若点N(a+5,a-2)在y轴上,则a=
,N点的坐标为
。
4.若点P(a,b)在第四象限内,则a,b的取值范围是(
)
A、a>0,b<0
B、a>0,b>0
C、a<0,b>0
D、a<0,b<0
5.如果点A(x,y)在第三象限,则点B(-x,y-1)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.点P在y轴左方、x轴上方,距y轴、x轴分别为3、4个单位长度,点P的坐标是(
)
A.(3,-4)
B.(-3,4)
C.(4,-3)
D.(-4,3)
7.已知点P(x,y)在第二象限,且,则点P的坐标为(
)
A.(-2,3)
B.(2,-3)
C.(-3,2)
D.(2,3)
7.如图,点A的坐标为(-3,4)。
(1)写出图中点B、C、D、E、F、G、H的坐标,并观察点A和C,点B和D有什么关系?
(2)在图中标出(-2,4)、(5,5)、(4,-3)三点的位置。
如图,在平面直角坐标系中表示下面各点:
A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0)
;H(-3,5)
(1)A点到原点O的距离是
;
(2)将点C向轴的负方向平移6个单位,
它与点
重合;
(3)连接CE,则直线CE与轴是什么关系?
(4)点F分别到、轴的距离是多少?
(5)观察点C与点E横纵坐标与位置的特点;
(6)观察点C与点H横纵坐标与位置的特点;
(7)观察点C与点D横纵坐标与位置的特点。
(二)、拓展探究
已知点P(2,3)。(1)在坐标平面内画出点P;(2)分别求出点P关于x轴、y轴的对称点P1、P2. (3)求三角形P1PP2的面积。
课题:7.1.3
平面直角坐标系习题课
【学习目标】
.加深对平面直角坐标系认识,熟悉用坐标表示点,能准确描出点的位置。
【学法指导】
由两条相互垂直、原点重合的数轴建立了平面直角坐标系。坐标平面内点与坐标的对应关系,顺利地实现由一维到二维的过渡,即由数字体现了点的位置,由点的位置体现了一种图形形状及大小,由抽象到具体。
【学习重点】进一步理解平面直角坐标系的相关概念及性质。
【自主学习】
1.平面直角坐标系的概念:平面内两条互相
、
重合的
组成的图形。其中,水平的数轴称为
或
,习惯上取向
为正方向;竖直的数轴称为
或
,习惯上取向
为方正向。两坐标轴的交点为平面直角坐标系的
,记为O,其坐标为
。有了平面直角坐标系,平面内的点就可以用一个
来表示,叫做点的坐标。建立平面直角坐标系后,平面被坐标轴分成四部分,分别叫
,
,
,
。坐标轴上的点不属于
。平面直角坐标系内一点A的坐标用(a,b)来表示,a是
坐标、b是
坐标这里的两个数据,一个表示水平方向与A点的距离,另一个表示竖直方向上到A点的距离。
2.各象限点的坐标的特点是:
⑴点P(x,y)在第一象限,则x
0,y
0.⑵点P(x,y)在第二象限,则x
0,y
0.
⑶点P(x,y)在第三象限,则x
0,y
0.⑷点P(x,y)在第四象限,则x
0,y
0。
3.坐标轴上点的坐标的特点是:
⑴点P(x,y)在x轴上,则x
,y
.
⑵点P(x,y)在y轴上,则x
,y
。
【合作探究一】
全班同学坐位均匀分布,不留走廊。以班内最中间的一个学生为原点,以这个学生所在的这一排为X轴,以这个学生所在列为Y轴,建立直角坐标系,由教师指定,并回答下列问题。
1、请在一、二、三、四象限内同学分别站起来,说出各自的坐标。
2、请在坐标上的同学分别站起来,并说出两轴上的点的坐标的特征;
X轴上的点:
Y轴上的点:
3、任选一行,那些同学所在直线与两轴平行(垂直),并说出该直线上的点的坐标特征。
(1)与X轴平行的点:
(2)与Y轴平行的点:
4、请每位同学找出你关于X(Y、原点)对称的同学,并说出关于两轴及原点的对称点的坐标特征:
(1)关于X轴的对称点:
(2)关于Y轴的对称点:
(3)关于原点的对称点:
5、请在坐标系的角平分线上的同学,并说出各自的特征:
(1)一、二象限的角平分线上:
(2)三、四象限的角平分线上:
【合作探究二】
探索:你知道下面两点和连线与坐标轴的关系吗?画一画,找一找。
⑴当≠0时,线段
y轴。
即当两个点的横坐标相同时,这两个点的连线
y轴。
⑵当≠0时,线段
x轴。
即当两个点的纵坐标相同时,这两个点的连线
x轴。
即时反馈:
1.已知坐标平面内点M(a,b)在第三象限,那么点N(b,-a)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知点A(2,-3),线段AB与坐标轴没有交点,则点B的坐标可能是
(
)
A.(-1,-2)
B.(
3,-2)
C.(1,2)
D.(-2,3)
3.点P(m+3,
m+1)在直角坐标系的x轴上,则点P坐标为(
)
A.(0,-2)
B.(
2,0)
C.(
4,0)
D.(0,-4)
4.已知点A(2,-3),线段AB与坐标轴平行,则点B的坐标可能是
(
)
A.(-1,-2)
B.(
3,-2)
C.(1,2)
D.(-2,-3)
5.如图,在直角坐标系中,,,.
求:的面积。
【课堂小结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
【达标测评】
1.若点P(2,k-1)在第一象限,则k
的取值范围是_______。
2.点P(m2-1,
m+3)在直角坐标系的y轴上,则点P坐标为
。
3.已知AB∥x轴,A点的坐标为(3,2),且AB=4,则B点的坐标为
。
4.已知点P(x,
|x|),则点P一定(
)
A.在第一象限
B.在第一或第四象限
C.在x轴上方
D.不在x轴下方
5.若点P(x,y)的坐标满足xy=0(x≠y),则点P在(
)
A.原点上
B.x轴上
C.y轴上
D.x轴上或y轴上
6.点E与点F的纵坐标相同,横坐标不同,则直线EF与y轴的关系是(
)
A.相交
B.垂直
C.平行
D.以上都不正确
7.建立适当的平面直角坐标系,表示边长为4的正方形各点的坐标。
8.如图,将边长为1的正三角形沿轴正方向连续翻转2008次,点在X轴上依次落在点,……,的位置,求点,的坐标.
【课后练习】
(一)、基础练习
1.若点A的坐标是(-3,5),则它到x轴的距离是
,到y轴的距离是
。
2.点B在x轴下方,y轴右侧,距y轴、x轴分别是2、4个单位长度,点B的坐标是
。
3.点P(a-1,a
2-9)在x轴负半轴上,则P点坐标是 。
4.
在平面直角坐标系中,适合条件∣x∣=6,
∣x-y∣=8的点p(x,y)的个数是(
)
A.2
B.3
C.4
D.5
5.已知点P(a,b),ab>0,a+b<0,则点P在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.在平面直角坐标系中,若A(-2,3),B(2,-3),则点A与点B(
)
A.关于x轴对称
B.
关于y轴对称
C.
关于原点对称
D.以上都不对
7、在直角坐标系中有两个点C、D,且CD⊥X轴,那么C、D两点的横坐标(
)
A、不相等
B、互为相反数
C、相等
D、相等或互为相反数
8、已知P(-2,3)则P点关于X轴的对称点P1的坐标为
,P点关于一、三象限的角平分线上的对称点P2的坐标为
。
(二)、拓展探究
1、画出以A(0,0)
,B(5,0)
,
C(6,4),
D(1,4)
为顶点的四边形ABCD,并求其面积。
2、如图,已知:A(3,2),B(5,0),E(4,1),求△AOE的面积。
3、在平面直角坐标系中,点A(0,3),B(0,-2),点C在x轴上,如果△ABC的面积是15,求点C的坐标。
课题:7.2.1
用坐标表示地理位置
【学习目标】
1、了解用平面直角坐标系来表示地理位置的意义及主要过程,能用坐标系来描述地理位置。
2、通过学习用坐标表示地理位置,培养解决实际问题的能力,发展空间观念。
【学习重点】利用坐标表示地理位置。
【学习难点】建立适当的坐标系表示地理位置。
【自主学习】
1.如图(图1),这是某市部分简图。
(1)请以火车站为坐标原点建立平面直角坐标系,并分别写出各地的坐标。
(2)改变坐标原点,重新建立一个平面直角坐标系,并写出各地坐标。
(图1)
(图2)
4.不管是出差办事,还是出去旅游,人们都愿意带上一幅地图,它给人们出行带来了很大方便.如(图2):这是北京市地图的一部分,你知道怎样用坐标表示地理位置吗?
【合作探究】
(一)探究用坐标表示地理位置的方法
1.根据以下条件画一幅示意图,标出学校和小刚家、小强家、小敏家的位置.
小刚家:出校门向东走1500
m,再向北走2000
m.
小强家:出校门向西走2000
m,再向北走3500
m,最后再向东走500
m.
小敏家:出校门向南走1000
m,再向东走3000
m,最后向南走750
m.
问题1:如何建立平面直角坐标系呢?以何参照点为原点?如何确定x轴、y轴?怎样确定单位长度呢?
解:如(图3):以
为坐标原点,以正东、正北方向为
轴、
轴正方向建立直角坐标系,取一个单位长度代表
米,则小刚家(
,
),小强家(
,
)小敏家(
,
)。
(图3)
(图4)
问题2:选取学校所在位置为原点,并以正东、正北方向为x轴、y轴的正方向有什么优点?
小结:利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程如下:
(1)建立坐标系,选择一个____________为原点,确定x轴、y轴的___方向;
(2)根据具体问题确定______________;
(3)在坐标平面内画出这些点,写出各点的_______和各个地点的名称.
即时反馈:
根据以下条件画一幅示意图,标出某一公园的各个景点.【请在(图4)上完成】
菊花园:从中心广场向北走150米,再向东走150米;
湖心亭:从中心广场向西走150米,再向北走100米;
松风亭:从中心广场向西走100米,再向南走50米;
育德泉:从中心广场向北走200米.
(二)探究表示地理位置的其他方法
即时反馈:
教材第75页:练习
第2题
【反思总结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?(小组交流,互助解决)
【达标测评】
1.如图,若在象棋盘上建立直角坐标系,使帅位于点(-1,-2).馬位于点(2,-2),则兵位于点
2.以百色汽车总站为坐标原点,向阳路为y轴建立直角坐标系,百色起义纪念馆位置如图所示,则其所覆盖的坐标可能是( )
A、(-5,3)B、(4,3)C、(5,-3)D、(-5,-3)
3.以下是甲、乙、丙三人看地图时对四个地标的描述:
甲:从学校向北直走500公尺,再向东直走100公尺可到图书馆.
乙:从学校向西直走300公尺,再向北直走200公尺可到邮局.
丙:邮局在火车站西方200公尺处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站( )
A、向南直走300公尺,再向西直走200公尺
B、向南直走300公尺,再向西直走600公尺
C、向南直走700公尺,再向西直走200公尺
D、向南直走700公尺,再向西直走600公尺
4.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是
5.王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,-2),你能帮她求出其他各景点的坐标吗?
【课后练习】
(一)、基础练习
1.利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程为:
⑴建立坐标系,选择一个适当的______为原点,确定x轴、y轴的_______;
⑵确定适当的_______,在坐标轴上标出单位长度;
⑶在坐标平面内画出这些点,写出各点的_______和各个地点的________。
2.图是某乡镇的示意图(图中每个小正方形的边长均为个单位长度)。
⑴试建立直角坐标系,用坐标表示各地的位置:
⑵如果已知王马村的坐标是(0,0),请用坐标表示出大山镇、爱心中学的位置。
⑶如果已知映月湖的坐标是(6,-3),请用坐标表示出大山镇、红旗乡的位置。
(二)、拓展探究
张先生手中有一张残缺不全的旧地图,依稀可见钟楼坐标A(4,-2),街口坐标B(4,2),资料记载张先生祖居坐标C(1,-2)。你能帮张先生找到他家的老屋吗?
课题:7.2.2
用坐标表示平移
【学习目标】
1.掌握坐标变化与图形平移的关系;能利用点的平移规律将平面图形进行平移;会根据图形上点的坐标的变化,来判定图形的移动过程.
2.
培养探究的兴趣和归纳概括的能力,发展学生的形象思维能力,和数形结合的意识.
【学习重点】掌握坐标变化与图形平移的关系;
【学习难点】利用坐标变化与图形平移的关系解决实际问题。
【自主学习】
问题:请同学们回忆前面我们学移知识,什么叫平移?图形的平移有哪些性质?
【合作探究一】
画图观察:在图中描出点A(-2,-3)作以下平移,请在图上标出平移后的点并写它们的坐标。
A(-2,-3)向右平移5个单位得到A2(
,
)
A(-2,-3)向左平移3个单位得到A3(
,
)
A(-2,-3)向右平移5个单位得到A4(
,
)
A(-2,-3)向右平移5个单位得到A5(
,
)
观察平移前后点的坐标的变化,你能从中发现什么规律?归纳“图形平移与点的坐标变化”之间的关系
(1)左、右平移:
原图形上的点(x,y)
(
)
原图形上的点(x,y)
(
)
(2)上、下平移:
原图形上的点(x,y)
(
)
原图形上的点(x,y)
(
)
即时反馈:
1.在平面直角坐标系中,有一点P(-4,2),若将点P:
(1)向左平移2个单位长度,所得点的坐标为_____________;
(2)向右平移3个单位长度,所得点的坐标为_____________;
(3)向下平移4个单位长度,所得点的坐标为_____________;
(4)向上平移5个单位长度,所得点的坐标为_____________;
2.已知A(1,4),B(-4,0),C(2,0)。
⑴将△ABC向左平移三个单位后,点A、B、C的坐标
分别变为
,
,
。
⑵将△ABC向下平移三个单位后,点A、B、C的坐标
分别变为
,
,
。
3、思考并归纳“点的坐标变化与图形平移”之间的关系
(1)横坐标变化,纵坐标不变:
原图形上的点(x,y)
向
平移
个单位
原图形上的点(x,y)
向
平移
个单位
(2)横坐标不变,纵坐标变化:
原图形上的点(x,y)
向
平移
个单位
原图形上的点(x,y)
向
平移
个单位
即时反馈:
1.已知A(1,4),B(-4,0),C(2,0)。
⑴将△ABC三顶点A、B、C的横坐标都增加2,相应的新图形就是把原图形向
平移了
个单位长度。
⑵将△ABC三顶点A、B、C的纵坐标都增加3,相应的新图形就是把原图形向
平移了
个单位长度。
⑶将△ABC三顶点A、B、C的横坐标都减少3,纵坐标都减少4相应的新图形就是把原图形先向
平移了
个单位长度,再向
平移了
个单位长度。
2.如图,三角形ABC中任意一点经平移后对应点为,将三角形ABC作同样的平移得到三角形.画出三角形,并写出三个顶点的坐标.
【合作探究二】
1、做一做,如图
(1)请写出点A的坐标;
(2)分别作出点A关于x轴、y轴的对称点,并写出它们的坐标,记为A2,A3;
(3)观察一下,点A与A2,点A与A3的坐标,有什么特别之处吗,你有什么发现呢?(哪些变了,哪些没变?)
观察点A2和点的位置,它们可看作关于哪个点对称?它们的坐标有什么关系?
归纳:A
A2(关于x轴对称),
不变,纵坐标
。
A
A3
(关于y轴对称)纵坐标
,
互为相反数。
(5)如果改变点A的坐标,这个规律仍然成立吗?你能否用字母来表示一下这个规律呢?
在直角坐标系中,点(a,b)关于x轴的对称点的坐标为
,关于y轴的对称点的坐标为
。
【课堂小结】
本节课你学到了什么?有什么收获和体会?还有什么困惑?
【达标测评】
1、能完成坐标平面内的点的平移时,坐标是如何变化的吗?填写下图(h>0):
(a,
)
向上平移h个单位
向左平移h个单位
向右平移h个单位
(
,b)
(a,b)
(
,b)
向下平移h个单位
(a,
)
难点透释:图形平移与坐标变化的关系
图像左右平移,纵坐标不变,横坐标左(移)减右(移)加;
图像上下平移,横坐标不变,纵坐标下(移)减上(移)加。
2、已知点M(-4,2),将点先向下平移3个单位长度,再向左平移3个单位长度,则点M在坐标系内的坐标为
.
3、平面直角坐标系中△ABC三个顶点的横坐标保持不变,
纵坐标都减去了3,则得到的新三角形与原三角形相比向
平移了
个单位。
4、在平面直角坐标系中,将点(2,1)向右平移3个单位长度,可以得到对应点坐标
;将点(2,-1)向左平移3个单位长度可得到对应点坐标
;
将点(2,5)向上平移3单位长度可得对应点坐标
;将点(-2,5)向下平移3单位长度可得对应点坐标
。
5、线段AB两端点坐标分别为A(-1,4),B(-4,1),现将它向左平移4个单位长度,得到线段A1B1,则A1、B1的坐标依次分别为(
)
A.(-5,0),(-8,-3)
B.(3,7),(0,5)
C.(-5,4),(-8,1)
D.(3,4),(0,1)
6、坐标系中,将正方形向上平移3个单位后,得到的正方形各顶点与原正方形各顶点坐标相比(
)
A.横坐标不变,纵坐标加3
B.纵坐标不变,横坐标加3
C.横坐标不变,纵坐标乘以3
D.纵坐标不变,横坐标乘以3
7、如图,小鱼的“嘴巴”所在的坐标是(1,1),请画出图形并回答下列问题。
⑴小鱼沿x轴向左平移6个单位,此时小鱼的“嘴巴”所在的坐标是多少?
⑵小鱼沿y轴向下平移4个单位,此时小鱼的“嘴巴”所在的坐标是多少?
8、将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1,
画出图形并写出点A1、B1、C1的坐标。
9、在平面直角坐标系中,将坐标(0,0),(2,4),(4,4),(2,0)的点用线段依次连接起来形成一个图案:
⑴这四个点的纵坐标若保持不变,横坐标变成原来的一半,将所得的四个点用线段依次连接起来,所得的图案与原图案相比有什么变化?请在平面直角坐标系中画出图形。
⑵纵坐标保持不变,横坐标分别加1呢?
课题:平面直角坐标系全章复习
一、本章知识结构图
二、本章知识梳理
1.有序数对:用含有
的词表示一个确定的位置,其中各个数表示
的含义,我们把这种有
的
个数a与b组成的数对,叫做有序数对,记作
。
2.平面直角坐标系的概念:平面内两条互相
、
重合的
组成的图形。
3.各象限点的坐标的特点是:
⑴点P(x,y)在第一象限,则x
0,y
0.⑵点P(x,y)在第二象限,则x
0,y
0.
⑶点P(x,y)在第三象限,则x
0,y
0.⑷点P(x,y)在第四象限,则x
0,y
0。
4.坐标轴上点的坐标的特点是:
⑴点P(x,y)在x轴上,则x
,y
.⑵点P(x,y)在y轴上,则x
,y
。
5.比例尺是图距与
的比。
6.利用平面直角坐标系来表示地理位置的一般步骤是:
⑴建立坐标系,选择一个适当的参照点为____,确定X轴、Y轴的______。
⑵根据具体问题确定适当的_______,在坐标轴上标出_______。
⑶在坐标平面内画出这些点,写出各点的______和各个地点的名称。
7.图形平移与点的坐标变化之间的关系(其中a、b为正数)
(1)左、右平移:
原图形上的点(x,y)
(
)
原图形上的点(x,y)
(
)
(2)上、下平移:
原图形上的点(x,y)
(
)
原图形上的点(x,y)
(
)
8.点的坐标变化与图形平移之间的关系(其中a、b为正数)
(1)横坐标变化,纵坐标不变:
原图形上的点(x,y)
向
平移
个单位
原图形上的点(x,y)
向
平移
个单位
(2)横坐标不变,纵坐标变化:
原图形上的点(x,y)
向
平移
个单位
原图形上的点(x,y)
向
平移
个单位
9.一、三象限的角平分线上的点:x=y;二、四象限的角平分线上的点:
平行于x轴的直线上的点
相等,平行于y轴的直线上的点
相等。
点P(x,y)
关于x轴的对称点
;关于y轴的对称点
。
关于原点的对称点
距离计算:
点P(a,b)到x轴的距离为_____,到y轴的距离为_____,到原点的距离为_____。
A(a,0),B(c,0)间的距离=____;A(0,b),B(0,d)间的距离=______;
A(a,0),B(0,d)
间的距离=________;A(a,b),B(c,d)间的距离=______。
三、巩固练习
1.将点P(-2,3)向右平移3个单位,再向下平移5
个单位,所得的点的坐标为
。
2.点P到x轴、y轴的距离分别是2、1,则点P的坐标可能为
。
3.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的坐标是
。
4.点P(x,y)满足xy>0,则点P在(
)
A.第一象限
B.
第二象限
C.
第三象限
D.
第一象限和第三象限
5.已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为(
)
A.3
B.1
C.0
D.-1
6.平面内点的坐标是(
)
A.一个点
B.一个图形
C.一个数
D.一个有序数对
7.在平面直角坐标系内,下列说法错误的是(
)
A.原点O不在任何象限内
B.原点O的坐标是0
C.原点O既在X轴上也在Y轴上
D.原点O在坐标平面内
8.X轴上的点P到Y轴的距离为2,则点P的坐标为(
)
A.(2,0)
B.(-2,0)
C.(0,2)
D.(2,0)或(-2,0)
9.三角形ABC三个顶点的坐标分别是
A(4,3)B(3,1)C(1,2),请你在平面直角坐标系中描出这个三角形,然后先将其向左平移4个单位,再将其向下平移2个单位,画出平移后的图形并写出相应顶点的坐标。
10.如图,写出三角形ABC各顶点的坐标并且求出三角形的面积。
四、课后练习
(一)、基础练习
1.有序数对(3,2)表示第3列第2排的座位,则位于第5列第4排的座位应记作(
)
A.(4,5)
B.(5,4)
C.(5、4)
D.(4、5)
2.在平面直角坐标系中,对于坐标P(2,5),下列说法错误的是(
)
A.P(2,5)表示这个点在平面内的位置
B.点P的纵坐标是5
C.它与点(5,2)表示同一个坐标
D.点P到x轴的距离是5
3.在平面直角坐标系中,点C(-2,4)向右平移3个单位后得到D点,则D点的坐标是(
)
A.(1,4)
B.(-5,4)
C.(-2,7)
D.(-2,1)
4.下列坐标所表示的点中,距离坐标系的原点最近的是
(
)
A.(-1,1)
B.(2,1)
C.(0,2)
D.(0,-2)
5.在平面直角坐标系中,若以点A(0,-3)为圆心,5为半径画一个圆,则这个圆与y轴的负半轴相交的点坐标是(
)
A.(8,0)
B.(
0,-8)
C.(0,8)
D.(-8,0)
6.已知x轴上的点P到y
轴的距离是3,则点P坐标是________
_。
7.已知点A(2,-3),若将点A向左平移3个单位得到点B,则点B坐标是_____
_,若将点A向上平移4个单位得到点C,则点C坐标是____
__。
在坐标轴上与点M(3,-4)距离等于5的点,共有几个?并求出这几个坐标
9.平面内有A、B、C、D、E共5个点。
⑴请建立适当的平面直角坐标系,写出A、B、C、D、E的坐标;
⑵以线段AB为一边,画出一个平行四边形。
10.现有一张利用平面直角坐标系画出来的某公园景区地图,如图,若知道游乐园D的坐标为(2,-2)。
⑴请按题意建立平面直角坐标系,写出其他景点的坐标;
⑵请指出距离原点最近和最远的景点。
二、拓展探究
如图,是两个五子棋爱好者对弈图(甲执黑子先行,乙执白子后走),观察棋盘,若点M的位置记作(3,D),
乙必须在哪个位置上落子,才不会让甲在短时间内获胜?为什么?
图1
图3
图2
图1
图1
_
B
_
A
_
C
_
D
_
E
_
G
_
F
图(2)
图2
B
A
北
60°
救生船
遇险船
·A
·B
向右平移a个单位
向左平移a个单位
向上平移b个单位
向下平移b个单位
(x+a,y)
(x-a,y)
(x,y+b)
(x,y-b)
向右平移a个单位
向左平移a个单位
向上平移b个单位
向下平移b个单位
(x+a,y)
(x-a,y)
(x,y+b)
(x,y-b)
M
多一份睿智
少一份嬉戏
展一份风采
审核人:
复核人:
