第三章圆单元检测卷
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
【2017年新北师大版数学九年级下】
第三章《圆》单元检测卷
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共36分)
1.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积为( ).
A.4π B.9π C.16π D.25π
2.如果一个扇形的半径是1,弧长是,那么此扇形的圆心角的大小为( )
A.30° B.45° C.60° D.90°
3.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是( )
A.相切 B.相离 C.相离或相切 D.相切或相交
4.如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )21教育名师原创作品
A.cm B.10cm C.8cm D.cm
5.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
6.如图,以点P为圆心,以为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为( )
A.(4,) B.(4,2) C.(4,4) D.(2,)
7.点P是⊙O外一点,PA、PB分别切⊙O于点A、B,∠P=70°,点C是⊙O上的点(不与点A、B重合),则∠ACB等于( )
A.70° B.55° C.70°或110° D.55°或125°
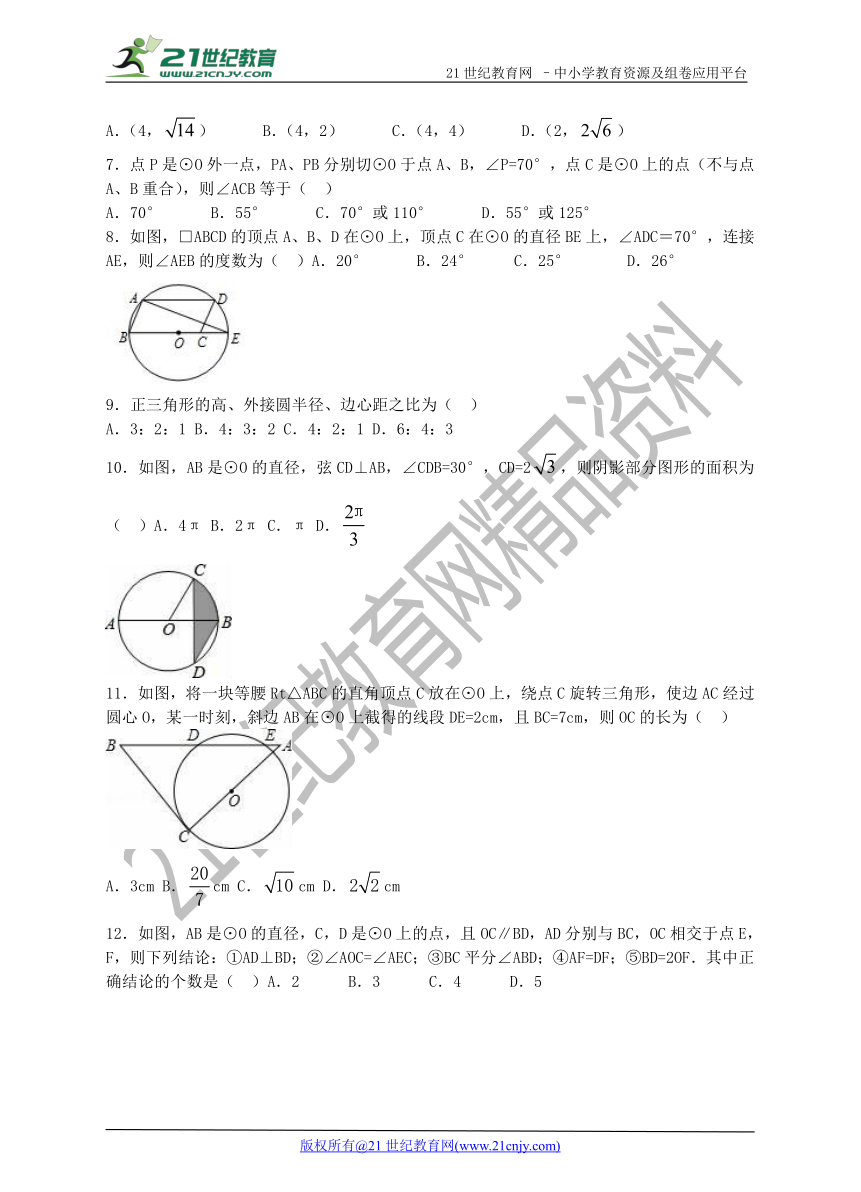
8.如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接AE,则∠AEB的度数为( )A.20° B.24° C.25° D.26°
9.正三角形的高、外接圆半径、边心距之比为( )
A.3:2:1 B.4:3:2 C.4:2:1 D.6:4:3
10.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则阴影部分图形的面积为( )A.4π B.2π C.π D.
11.如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
A.3cm B.cm C.cm D.cm
12.如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF.其中正确结论的个数是( )A.2 B.3 C.4 D.521*cnjy*com
二、填空题:(每小题3分共12分)
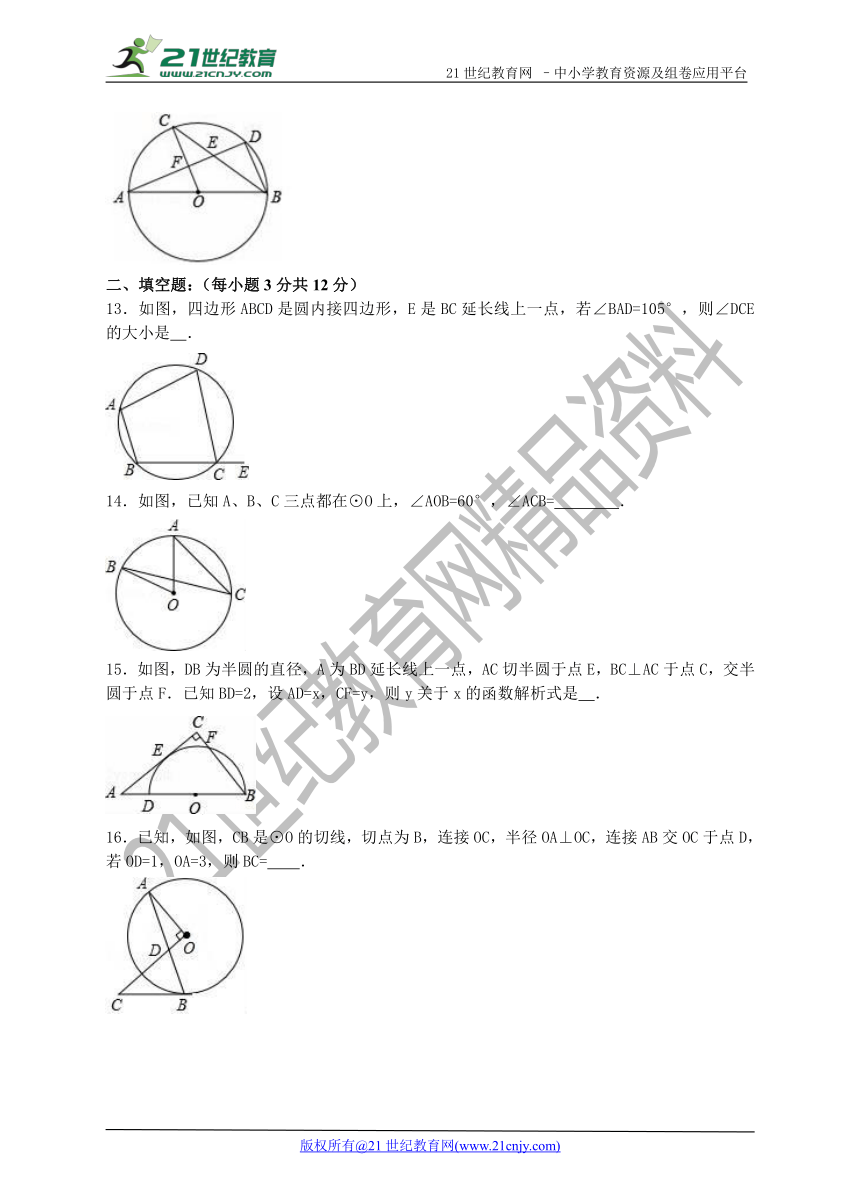
13.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是 .21教育网
14.如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB= .
15.如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是 .
16.已知,如图,CB是⊙O的切线,切点为B,连接OC,半径OA⊥OC,连接AB交OC于点D,若OD=1,OA=3,则BC= .21世纪教育网版权所有
三、解答题:(共52分)
17.(5分)如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
18.(6分)如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.
19.(8分)如图,BE是⊙O的直径,半径OA⊥弦BC,点D为垂足,连AE,EC.
(1)若∠AEC=28°,求∠AOB的度数;
(2)若∠BEA=∠B,BC=6,求⊙O的半径.
20.(8分)如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=1,BE=2,求AC的长.
21.(8分)如图,已知AB是⊙O的直径,弦AC∥OD.
(1)求证:.
(2)若的度数为,求∠AOD的度数.
22.(8分)如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.【来源:21cnj*y.co*m】
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
23.(9分)已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.21*cnjy*com
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
参考答案
1.C.
【解析】
试题分析:根据题意、利用圆的面积公式计算即可.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积是以5为半径的圆与以3为半径的圆组成的圆环的面积,即π×52﹣π×32=16π.2-1-c-n-j-y
故选:C.
2.C
【解析】
试题分析:设圆心角是n度,根据题意得
=,
解得:n=60.
故选:C.
3.D.
【解析】
试题分析:当OP垂直于直线l时,即圆心O到直线l的距离d=2=r,⊙O与l相切;当OP不垂直于直线l时,即圆心O到直线l的距离d<2=r,⊙O与直线l相交.所以直线l与⊙O的位置关系是相切或相交.故选D.
4.A.
【解析】
试题分析:连结OA,如图,设⊙O的半径为r,
∵OD⊥AB,
∴AC=BC=AB=8,
在Rt△OAC中,∵OA=r,OC=OD﹣CD=r﹣6,AC=8,
∴(r﹣6)2+82=r2,解得r=,
即⊙O的半径为cm.
故选A.
5.C.
【解析】
试题分析:由BD是⊙O的直径,根据直径所对的圆周角是直角,得∠BCD=90°,可求∠D=60°,即可求∠A=∠D=60°.故选C.www.21-cn-jy.com
6.C.
【解析】
试题分析:过点P作PC⊥AB于点C;
即点C为AB的中点,又点A的坐标为(2,0),点B的坐标为(6,0),故点C(4,0)
在Rt△PAC中,PA=,AC=2,即有PC=4,即P(4,4).
故选C.
7.D.
【解析】
试题分析:如图,∵PA、PB分别切⊙O于点A、B,∴∠OAP=∠OBP=90°,∵∠P=70°,∴∠AOB=110°,∴∠ACB=55°,当点C在劣弧AB上,∵∠AOB=110°,∴弧ACB的度数为250°,∴∠ACB=125°.故选D.【来源:21·世纪·教育·网】
8.A
【解析】
试题分析:根据平行四边形的性质可得:∠B=70°,根据BE为直径可得:∠BAE=90°,根据△ABE的内角和定理可得:∠AEB=180°-90°-70°=20°.【出处:21教育名师】
9.A.
【解析】
试题分析:如图,
△ABC是等边三角形,AD是高.点O是其外接圆的圆心,
由等边三角形的三线合一得点O在AD上,并且点O还是它的内切圆的圆心.
∵AD⊥BC,∠1=∠4=30°,
∴BO=2OD,而OA=OB,
∴AD=3OD,
∴AD:OA:OD=3:2:1,
故选A.
10.D
【解析】
试题分析:如图,假设线段CD、AB交于点E,∵AB是⊙O的直径,弦CD⊥AB,∴CE=ED=,又∵∠CDB=30°,21cnjy.com
∴∠COE=2∠CDB=60°,∠OCE=30°,∴OE=CE cot60°=×=1,OC=2OE=2,
∴S阴影=S扇形OCB﹣S△COE+S△BED=﹣OE×EC+BE ED=﹣+=.
故选D.
11.A
【解析】
试题分析:过O点作OM⊥AB,
∴ME=DM=1cm,
设MO=h,CO=DO=x,
∵△ABC为等腰直角三角形,AC=BC,
∴∠MAO=45°,
∴AO=h
∵AO=7-x,
∴ ,
在Rt△DMO中,
h2=x2-1,
∴2x2-2=49-14x+x2,解得:x=-17(舍去)或x=3,
故选A.
二、填空题()
12.C.
【解析】
试题分析:∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BD,故①正确;
∵∠ACE=∠DAB+∠EBA,∠AOC=2∠EBA,∴∠AOC≠∠AEC,故②不正确;
∵OC∥BD,∴∠OCB=∠CBD,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC=∠CBD,即BC平分∠ABD,故③正确;
∴OC⊥AD,∴AF=FD,故④正确;
∴OF为△ABD的中位线,∴BD=2OF,故⑤正确,综上可知正确的有4个,故选C.
13.105°.
【解析】
试题分析:∵四边形ABCD是圆内接四边形,∴∠DAB+∠DCB=180°,∵∠BAD=105°,∴∠DCB=180°﹣∠DAB=180°﹣105°=75°,∵∠DCB+∠DCE=180°,∴∠DCE=∠DAB=105°.
14.30°
【解析】
试题分析:由∠ACB是⊙O的圆周角,∠AOB是圆心角,且∠AOB=60°,根据圆周角定理,即可求得圆周角∠ACB的度数. 如图,∵∠AOB=60°, ∴∠ACB=∠AOB=30°.
15.
【解析】
试题分析:连接DF、OE,过点D作DG⊥AC于点G,先证明四边形CGDF是矩形,得出DG=CF=y;再证明△AOE∽△ADG,根据相似三角形的性质即可求出,即,化简可得y=.
16.4.
【解析】
试题分析:连接OB,
∵OA⊥OC,
∴∠A+∠ADO=90°,
∵CB是⊙O的切线,
∴∠OBC=90°,
∴∠OBD+∠CBD=90°,
∵AO=BO,
∴∠OAD=∠OBD,
∴∠OAD=∠OBD,
∴CB=CD,
设BC=x,则CD=x,
在Rt△OBC中,OB=OA=3,OC=OD+CD=x+1,
∵OB2+BC2=OC2,
∴32+x2=(x+1)2,
解得:x=4,
即BC的长为4,
故答案为:4.
17.
【解析】
试题分析:由OD⊥AB,根据垂径定理得到AC=BC=AB=4,设AO=x,则OC=OD﹣CD=x﹣2,在Rt△ACO中根据勾股定理得到x2=42+(x﹣2)2,解得x=5,则AE=10,OC=3,再由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.2·1·c·n·j·y
试题解析:连结BE,如图,
∵OD⊥AB,
∴AC=BC=AB=×8=4,
设AO=x,则OC=OD﹣CD=x﹣2,
在Rt△ACO中,∵AO2=AC2+OC2,
∴x2=42+(x﹣2)2,解得 x=5,
∴AE=10,OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=.
18.30°.
【解析】
试题分析:如图,连接OC. 构建直角△OCD和等边△OBC,结合图形,可以得到∠BCD=90°﹣∠OCB=30°.21·cn·jy·com
试题解析:如图,连接OC.
∵CD是⊙O的切线,
∴∠OCD=90°.
∵∠A=30°,
∴∴∠COB=2∠=60°.
∵OC=OB,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠BCD=90°﹣∠OCB=30°.
19.(1)56°;(2).
【解析】
试题分析:(1)根据垂径定理得到=,根据圆周角定理解答;
(2)根据圆周角定理得到∠C=90°,根据等腰三角形的性质得到∠B=30°,根据余弦的定义求出BE即可.www-2-1-cnjy-com
试题解析:(1)∵OA⊥BC,
∴=,
∴∠AEB=∠AEC=28°,
由圆周角定理得,∠AOB=2∠AEB=56°;
(2)∵BE是⊙O的直径,
∴∠C=90°,
∴∠CEB+∠B=90°,
∵∠BEA=∠B,∠AEB=∠AEC,
∴∠B=30°,
∴BE==,
∴⊙O的半径为.
20.8.
【解析】
试题分析:(1)根据等腰三角形的三线合一即可证明.
(2)由△BED∽△BAC,得,列出方程即可解决问题.
试题解析: (1)连结AE,如图,∵AC为⊙O的直径,
∴∠AEC=90°,∴AE⊥BC,而AB=AC,∴BE=CE.
(2)连结DE,如图,∵BE=CE=2,∴BC=4,∵∠BED=∠BAC,而∠DBE=∠CBA,
∴△BED∽△BAC,∴,即,∴BA=8,∴AC=BA=8.
21.(1)、证明过程见解析;(2)、119°.
【解析】
试题分析:(1)、连接OC,根据等腰三角形的性质得出∠OAC=∠ACO,根据平行线的性质得出∠OAC=∠BOD,∠DOC=∠ACO,从而得出∠BOD=∠COD,然后得出答案;(2)、根据弧AC的度数以及第一题的结论得出弧CD的度数,然后得出弧ACD的度数,从而求出圆心角的度数.
试题解析:(1)、连接OC.∵OA=OC,∴∠OAC=∠ACO.
∵AC∥OD,∴∠OAC=∠BOD.∴∠DOC=∠ACO.∴∠BOD=∠COD.∴.
(2)、∵,∴=,
, ∠AOD=119°
22.(1)证明见解析(2)1.6
【解析】
试题分析:(1)由AE=AB,可得∠ABE=90°﹣∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;【版权所有:21教育】
(2)首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=(180°﹣∠BAC=)=90°﹣∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣∠BAC)+∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线;
(2)连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴,
∵在Rt△ABC中,AB=8,BC=6,
∴AC==10,
∴,
解得:AD=6.4,
∵AE=AB=8,
∴DE=AE﹣AD=8﹣6.4=1.6.
23.(1)证明见试题解析;(2)(3)﹣π.
【解析】
试题分析:(1)连接OD,如图,利用等边三角形的性质得到∠A=∠C=60°,再证明OD∥BC,然后利用DF⊥BC可得OD⊥BC,再根据切线的判定定理可判断DF为⊙O的切线;
(2)利用等边三角形的性质得到AB=AC=4,∠C=60°,则CD=2,然后在Rt△CDF中利用正弦的定义可计算出DF;21·世纪*教育网
(3)连接OE,如图,根据扇形的面积公式,利用S阴影部分=S梯形ODFE﹣S扇形DOE进行计算.
试题解析:(1)连接OD,如图,∵△ABC为等边三角形,∴∠A=∠C=60°,
∵OA=OD,∴∠ODA=∠A=60°,∴∠ODA=∠C,∴OD∥BC,∵DF⊥BC,
∴OD⊥BC,∴DF为⊙O的切线;
(2)∵等边三角形ABC的边长为4,∴AB=AC=4,∠C=60°,∵AO=AD=2,
∴CD=2,在Rt△CDF中,∵sinC=,∴DF=2sin60°=;
(3)连接OE,如图,∵CF=CD=1,∴EF=CE﹣CF=1,
∴S阴影部分=S梯形ODFE﹣S扇形DOE=(1+2) ﹣=﹣π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
【2017年新北师大版数学九年级下】
第三章《圆》单元检测卷
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共36分)
1.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积为( ).
A.4π B.9π C.16π D.25π
2.如果一个扇形的半径是1,弧长是,那么此扇形的圆心角的大小为( )
A.30° B.45° C.60° D.90°
3.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是( )
A.相切 B.相离 C.相离或相切 D.相切或相交
4.如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )21教育名师原创作品
A.cm B.10cm C.8cm D.cm
5.如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
6.如图,以点P为圆心,以为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为( )
A.(4,) B.(4,2) C.(4,4) D.(2,)
7.点P是⊙O外一点,PA、PB分别切⊙O于点A、B,∠P=70°,点C是⊙O上的点(不与点A、B重合),则∠ACB等于( )
A.70° B.55° C.70°或110° D.55°或125°
8.如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接AE,则∠AEB的度数为( )A.20° B.24° C.25° D.26°
9.正三角形的高、外接圆半径、边心距之比为( )
A.3:2:1 B.4:3:2 C.4:2:1 D.6:4:3
10.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则阴影部分图形的面积为( )A.4π B.2π C.π D.
11.如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
A.3cm B.cm C.cm D.cm
12.如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF.其中正确结论的个数是( )A.2 B.3 C.4 D.521*cnjy*com
二、填空题:(每小题3分共12分)
13.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是 .21教育网
14.如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB= .
15.如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知BD=2,设AD=x,CF=y,则y关于x的函数解析式是 .
16.已知,如图,CB是⊙O的切线,切点为B,连接OC,半径OA⊥OC,连接AB交OC于点D,若OD=1,OA=3,则BC= .21世纪教育网版权所有
三、解答题:(共52分)
17.(5分)如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
18.(6分)如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.
19.(8分)如图,BE是⊙O的直径,半径OA⊥弦BC,点D为垂足,连AE,EC.
(1)若∠AEC=28°,求∠AOB的度数;
(2)若∠BEA=∠B,BC=6,求⊙O的半径.
20.(8分)如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=1,BE=2,求AC的长.
21.(8分)如图,已知AB是⊙O的直径,弦AC∥OD.
(1)求证:.
(2)若的度数为,求∠AOD的度数.
22.(8分)如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.【来源:21cnj*y.co*m】
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
23.(9分)已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.21*cnjy*com
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
参考答案
1.C.
【解析】
试题分析:根据题意、利用圆的面积公式计算即可.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积是以5为半径的圆与以3为半径的圆组成的圆环的面积,即π×52﹣π×32=16π.2-1-c-n-j-y
故选:C.
2.C
【解析】
试题分析:设圆心角是n度,根据题意得
=,
解得:n=60.
故选:C.
3.D.
【解析】
试题分析:当OP垂直于直线l时,即圆心O到直线l的距离d=2=r,⊙O与l相切;当OP不垂直于直线l时,即圆心O到直线l的距离d<2=r,⊙O与直线l相交.所以直线l与⊙O的位置关系是相切或相交.故选D.
4.A.
【解析】
试题分析:连结OA,如图,设⊙O的半径为r,
∵OD⊥AB,
∴AC=BC=AB=8,
在Rt△OAC中,∵OA=r,OC=OD﹣CD=r﹣6,AC=8,
∴(r﹣6)2+82=r2,解得r=,
即⊙O的半径为cm.
故选A.
5.C.
【解析】
试题分析:由BD是⊙O的直径,根据直径所对的圆周角是直角,得∠BCD=90°,可求∠D=60°,即可求∠A=∠D=60°.故选C.www.21-cn-jy.com
6.C.
【解析】
试题分析:过点P作PC⊥AB于点C;
即点C为AB的中点,又点A的坐标为(2,0),点B的坐标为(6,0),故点C(4,0)
在Rt△PAC中,PA=,AC=2,即有PC=4,即P(4,4).
故选C.
7.D.
【解析】
试题分析:如图,∵PA、PB分别切⊙O于点A、B,∴∠OAP=∠OBP=90°,∵∠P=70°,∴∠AOB=110°,∴∠ACB=55°,当点C在劣弧AB上,∵∠AOB=110°,∴弧ACB的度数为250°,∴∠ACB=125°.故选D.【来源:21·世纪·教育·网】
8.A
【解析】
试题分析:根据平行四边形的性质可得:∠B=70°,根据BE为直径可得:∠BAE=90°,根据△ABE的内角和定理可得:∠AEB=180°-90°-70°=20°.【出处:21教育名师】
9.A.
【解析】
试题分析:如图,
△ABC是等边三角形,AD是高.点O是其外接圆的圆心,
由等边三角形的三线合一得点O在AD上,并且点O还是它的内切圆的圆心.
∵AD⊥BC,∠1=∠4=30°,
∴BO=2OD,而OA=OB,
∴AD=3OD,
∴AD:OA:OD=3:2:1,
故选A.
10.D
【解析】
试题分析:如图,假设线段CD、AB交于点E,∵AB是⊙O的直径,弦CD⊥AB,∴CE=ED=,又∵∠CDB=30°,21cnjy.com
∴∠COE=2∠CDB=60°,∠OCE=30°,∴OE=CE cot60°=×=1,OC=2OE=2,
∴S阴影=S扇形OCB﹣S△COE+S△BED=﹣OE×EC+BE ED=﹣+=.
故选D.
11.A
【解析】
试题分析:过O点作OM⊥AB,
∴ME=DM=1cm,
设MO=h,CO=DO=x,
∵△ABC为等腰直角三角形,AC=BC,
∴∠MAO=45°,
∴AO=h
∵AO=7-x,
∴ ,
在Rt△DMO中,
h2=x2-1,
∴2x2-2=49-14x+x2,解得:x=-17(舍去)或x=3,
故选A.
二、填空题()
12.C.
【解析】
试题分析:∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BD,故①正确;
∵∠ACE=∠DAB+∠EBA,∠AOC=2∠EBA,∴∠AOC≠∠AEC,故②不正确;
∵OC∥BD,∴∠OCB=∠CBD,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC=∠CBD,即BC平分∠ABD,故③正确;
∴OC⊥AD,∴AF=FD,故④正确;
∴OF为△ABD的中位线,∴BD=2OF,故⑤正确,综上可知正确的有4个,故选C.
13.105°.
【解析】
试题分析:∵四边形ABCD是圆内接四边形,∴∠DAB+∠DCB=180°,∵∠BAD=105°,∴∠DCB=180°﹣∠DAB=180°﹣105°=75°,∵∠DCB+∠DCE=180°,∴∠DCE=∠DAB=105°.
14.30°
【解析】
试题分析:由∠ACB是⊙O的圆周角,∠AOB是圆心角,且∠AOB=60°,根据圆周角定理,即可求得圆周角∠ACB的度数. 如图,∵∠AOB=60°, ∴∠ACB=∠AOB=30°.
15.
【解析】
试题分析:连接DF、OE,过点D作DG⊥AC于点G,先证明四边形CGDF是矩形,得出DG=CF=y;再证明△AOE∽△ADG,根据相似三角形的性质即可求出,即,化简可得y=.
16.4.
【解析】
试题分析:连接OB,
∵OA⊥OC,
∴∠A+∠ADO=90°,
∵CB是⊙O的切线,
∴∠OBC=90°,
∴∠OBD+∠CBD=90°,
∵AO=BO,
∴∠OAD=∠OBD,
∴∠OAD=∠OBD,
∴CB=CD,
设BC=x,则CD=x,
在Rt△OBC中,OB=OA=3,OC=OD+CD=x+1,
∵OB2+BC2=OC2,
∴32+x2=(x+1)2,
解得:x=4,
即BC的长为4,
故答案为:4.
17.
【解析】
试题分析:由OD⊥AB,根据垂径定理得到AC=BC=AB=4,设AO=x,则OC=OD﹣CD=x﹣2,在Rt△ACO中根据勾股定理得到x2=42+(x﹣2)2,解得x=5,则AE=10,OC=3,再由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.2·1·c·n·j·y
试题解析:连结BE,如图,
∵OD⊥AB,
∴AC=BC=AB=×8=4,
设AO=x,则OC=OD﹣CD=x﹣2,
在Rt△ACO中,∵AO2=AC2+OC2,
∴x2=42+(x﹣2)2,解得 x=5,
∴AE=10,OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=.
18.30°.
【解析】
试题分析:如图,连接OC. 构建直角△OCD和等边△OBC,结合图形,可以得到∠BCD=90°﹣∠OCB=30°.21·cn·jy·com
试题解析:如图,连接OC.
∵CD是⊙O的切线,
∴∠OCD=90°.
∵∠A=30°,
∴∴∠COB=2∠=60°.
∵OC=OB,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠BCD=90°﹣∠OCB=30°.
19.(1)56°;(2).
【解析】
试题分析:(1)根据垂径定理得到=,根据圆周角定理解答;
(2)根据圆周角定理得到∠C=90°,根据等腰三角形的性质得到∠B=30°,根据余弦的定义求出BE即可.www-2-1-cnjy-com
试题解析:(1)∵OA⊥BC,
∴=,
∴∠AEB=∠AEC=28°,
由圆周角定理得,∠AOB=2∠AEB=56°;
(2)∵BE是⊙O的直径,
∴∠C=90°,
∴∠CEB+∠B=90°,
∵∠BEA=∠B,∠AEB=∠AEC,
∴∠B=30°,
∴BE==,
∴⊙O的半径为.
20.8.
【解析】
试题分析:(1)根据等腰三角形的三线合一即可证明.
(2)由△BED∽△BAC,得,列出方程即可解决问题.
试题解析: (1)连结AE,如图,∵AC为⊙O的直径,
∴∠AEC=90°,∴AE⊥BC,而AB=AC,∴BE=CE.
(2)连结DE,如图,∵BE=CE=2,∴BC=4,∵∠BED=∠BAC,而∠DBE=∠CBA,
∴△BED∽△BAC,∴,即,∴BA=8,∴AC=BA=8.
21.(1)、证明过程见解析;(2)、119°.
【解析】
试题分析:(1)、连接OC,根据等腰三角形的性质得出∠OAC=∠ACO,根据平行线的性质得出∠OAC=∠BOD,∠DOC=∠ACO,从而得出∠BOD=∠COD,然后得出答案;(2)、根据弧AC的度数以及第一题的结论得出弧CD的度数,然后得出弧ACD的度数,从而求出圆心角的度数.
试题解析:(1)、连接OC.∵OA=OC,∴∠OAC=∠ACO.
∵AC∥OD,∴∠OAC=∠BOD.∴∠DOC=∠ACO.∴∠BOD=∠COD.∴.
(2)、∵,∴=,
, ∠AOD=119°
22.(1)证明见解析(2)1.6
【解析】
试题分析:(1)由AE=AB,可得∠ABE=90°﹣∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;【版权所有:21教育】
(2)首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=(180°﹣∠BAC=)=90°﹣∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣∠BAC)+∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线;
(2)连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴,
∵在Rt△ABC中,AB=8,BC=6,
∴AC==10,
∴,
解得:AD=6.4,
∵AE=AB=8,
∴DE=AE﹣AD=8﹣6.4=1.6.
23.(1)证明见试题解析;(2)(3)﹣π.
【解析】
试题分析:(1)连接OD,如图,利用等边三角形的性质得到∠A=∠C=60°,再证明OD∥BC,然后利用DF⊥BC可得OD⊥BC,再根据切线的判定定理可判断DF为⊙O的切线;
(2)利用等边三角形的性质得到AB=AC=4,∠C=60°,则CD=2,然后在Rt△CDF中利用正弦的定义可计算出DF;21·世纪*教育网
(3)连接OE,如图,根据扇形的面积公式,利用S阴影部分=S梯形ODFE﹣S扇形DOE进行计算.
试题解析:(1)连接OD,如图,∵△ABC为等边三角形,∴∠A=∠C=60°,
∵OA=OD,∴∠ODA=∠A=60°,∴∠ODA=∠C,∴OD∥BC,∵DF⊥BC,
∴OD⊥BC,∴DF为⊙O的切线;
(2)∵等边三角形ABC的边长为4,∴AB=AC=4,∠C=60°,∵AO=AD=2,
∴CD=2,在Rt△CDF中,∵sinC=,∴DF=2sin60°=;
(3)连接OE,如图,∵CF=CD=1,∴EF=CE﹣CF=1,
∴S阴影部分=S梯形ODFE﹣S扇形DOE=(1+2) ﹣=﹣π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
