第7章 平面图形的认识(二) 单元复习卷(含答案)
文档属性
| 名称 | 第7章 平面图形的认识(二) 单元复习卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-10 13:51:00 | ||
图片预览


文档简介
第7章
平面图形的认识(二)复习卷
(时间:90分钟
满分:100分)
班级_______
姓名_______
得分_______
一、选择题(每小题2分,共20分)
1.平移改变图形的
(
)
A.位置
B.大小
C.形状
D.位置、大小和形状
2.图中三角形的个数是
(
)
A.2
B.3
C.4
D.5
3.一个多边形的内角和等于1260°,那么它是
(
)
A.六边形
B.七边形
C.八边形
D.九边形
4.经过平移,图形上每个点都沿同一个方向移动了一段距离,则不同的点移动的距离(
)
A.不同
B.既可能相同也可能不同
C.相同
D.无法确定
5.一个多边形的每一个内角均为108°,则这个多边形是
(
)
A.七边形
B.六边形
C.五边形
D.四边形
6.如图,下列条件:
①∠1+∠2=180°;②∠1=∠2;③∠3+∠4=180°;④∠3=∠4;⑤∠1+∠2=90°;⑥∠3+∠4=90°.其中,能判断直线l1∥l2的有
(
)
A.1个
B.2个
C.3个
D.4个
7.有3
cm,6
cm,8
cm,9
cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为
(
)
A.1
B.2
C.3
D.4
8.下列说法中正确的是
(
)
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
9.如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为
(
)
A.40°
B.35°
C.50°
D.45°
10.如果两个角的一边在同一条直线上,另一条边互相平行,那么这两个角的关系为
(
)
A.相等
B.互补
C.相等且互补
D.相等或互补
二、填空题(每小题3分,共24分)
11.一个多边形的每一个外角都等于30°,则这个多边形的内角和是_______
12.如图,与∠1成同位角的角有_______个,与∠1成内错角的角有_______个,与∠1成同旁内角的角有_______个.
13.如图所示的图形中x的值是_______.
14.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B=_______度.
15.如图,∠1=88°,∠2=88°,∠3=50°,则∠4=_______.
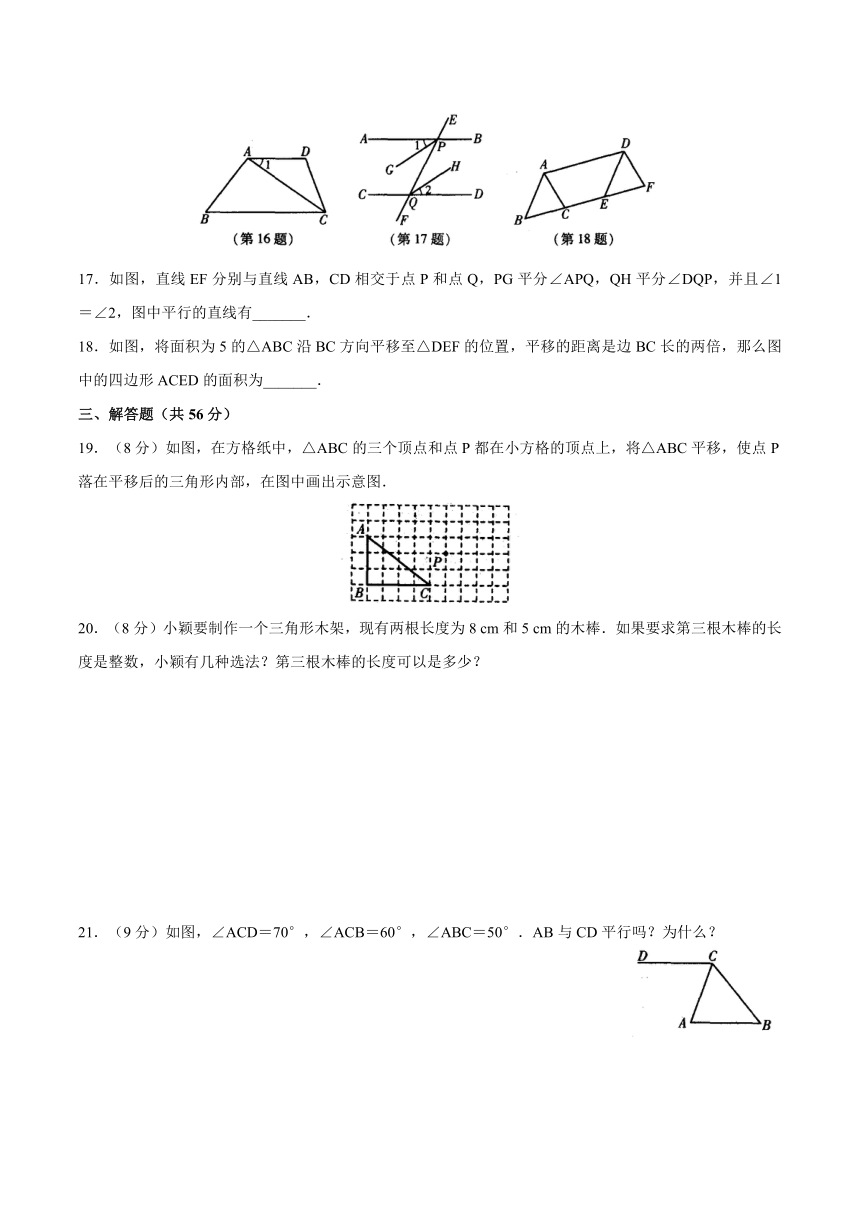
16.如图,四边形ABCD中,BC∥AD,∠BCA=∠DCA,∠1=35°,则∠D=_______.
17.如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,图中平行的直线有_______.
18.如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为_______.
三、解答题(共56分)
19.(8分)如图,在方格纸中,△ABC的三个顶点和点P都在小方格的顶点上,将△ABC平移,使点P落在平移后的三角形内部,在图中画出示意图.
20.(8分)小颖要制作一个三角形木架,现有两根长度为8
cm和5
cm的木棒.如果要求第三根木棒的长度是整数,小颖有几种选法?第三根木棒的长度可以是多少?
21.(9分)如图,∠ACD=70°,∠ACB=60°,∠ABC=50°.AB与CD平行吗?为什么?
22(9分)如图,AB∥CD,AD∥BC,∠B与∠D相等吗?试说明理由.
23.(10分)如图,△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC,∠DAE与(∠C-∠B)相等吗?试说明理由.
24.(12分)如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
(1)当动点P落在第①部分时,试说明∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)
(3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点
P的具体位置和相应的结论.选择其中一种结论加以证明.
参考答案
1.A
2.D
3.D
4.C
5.C
6.B
7.C
8.D
9.A
10.D
11.1800°
12.3
2
2
13.60
14.60
15.130°
16.110°
17.AB//CD,PG//QH
18.15
19.如图
20.小颖有9种选法.第三根木棒的长度可以是4
cm,5
cm,6
cm,7
cm,8
cm.9
cm,10
cm,11
cm,12
cm.
21.AB//CD.
22.∠B=∠D
23.相等
24.(1)略
(2)不成立.(3)①当动点P在射线BA的右侧时(如图乙),结论是∠PBD=∠PAC+∠APB.②当动点P在射线BA上时(如图丙),结论是∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD(任写一个即可).③当动点P在射线BA的左侧时(如图丁),结论是∠PAC=∠APB+∠PBD.
平面图形的认识(二)复习卷
(时间:90分钟
满分:100分)
班级_______
姓名_______
得分_______
一、选择题(每小题2分,共20分)
1.平移改变图形的
(
)
A.位置
B.大小
C.形状
D.位置、大小和形状
2.图中三角形的个数是
(
)
A.2
B.3
C.4
D.5
3.一个多边形的内角和等于1260°,那么它是
(
)
A.六边形
B.七边形
C.八边形
D.九边形
4.经过平移,图形上每个点都沿同一个方向移动了一段距离,则不同的点移动的距离(
)
A.不同
B.既可能相同也可能不同
C.相同
D.无法确定
5.一个多边形的每一个内角均为108°,则这个多边形是
(
)
A.七边形
B.六边形
C.五边形
D.四边形
6.如图,下列条件:
①∠1+∠2=180°;②∠1=∠2;③∠3+∠4=180°;④∠3=∠4;⑤∠1+∠2=90°;⑥∠3+∠4=90°.其中,能判断直线l1∥l2的有
(
)
A.1个
B.2个
C.3个
D.4个
7.有3
cm,6
cm,8
cm,9
cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为
(
)
A.1
B.2
C.3
D.4
8.下列说法中正确的是
(
)
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
9.如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为
(
)
A.40°
B.35°
C.50°
D.45°
10.如果两个角的一边在同一条直线上,另一条边互相平行,那么这两个角的关系为
(
)
A.相等
B.互补
C.相等且互补
D.相等或互补
二、填空题(每小题3分,共24分)
11.一个多边形的每一个外角都等于30°,则这个多边形的内角和是_______
12.如图,与∠1成同位角的角有_______个,与∠1成内错角的角有_______个,与∠1成同旁内角的角有_______个.
13.如图所示的图形中x的值是_______.
14.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B=_______度.
15.如图,∠1=88°,∠2=88°,∠3=50°,则∠4=_______.
16.如图,四边形ABCD中,BC∥AD,∠BCA=∠DCA,∠1=35°,则∠D=_______.
17.如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,图中平行的直线有_______.
18.如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为_______.
三、解答题(共56分)
19.(8分)如图,在方格纸中,△ABC的三个顶点和点P都在小方格的顶点上,将△ABC平移,使点P落在平移后的三角形内部,在图中画出示意图.
20.(8分)小颖要制作一个三角形木架,现有两根长度为8
cm和5
cm的木棒.如果要求第三根木棒的长度是整数,小颖有几种选法?第三根木棒的长度可以是多少?
21.(9分)如图,∠ACD=70°,∠ACB=60°,∠ABC=50°.AB与CD平行吗?为什么?
22(9分)如图,AB∥CD,AD∥BC,∠B与∠D相等吗?试说明理由.
23.(10分)如图,△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC,∠DAE与(∠C-∠B)相等吗?试说明理由.
24.(12分)如图,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)
(1)当动点P落在第①部分时,试说明∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)
(3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点
P的具体位置和相应的结论.选择其中一种结论加以证明.
参考答案
1.A
2.D
3.D
4.C
5.C
6.B
7.C
8.D
9.A
10.D
11.1800°
12.3
2
2
13.60
14.60
15.130°
16.110°
17.AB//CD,PG//QH
18.15
19.如图
20.小颖有9种选法.第三根木棒的长度可以是4
cm,5
cm,6
cm,7
cm,8
cm.9
cm,10
cm,11
cm,12
cm.
21.AB//CD.
22.∠B=∠D
23.相等
24.(1)略
(2)不成立.(3)①当动点P在射线BA的右侧时(如图乙),结论是∠PBD=∠PAC+∠APB.②当动点P在射线BA上时(如图丙),结论是∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD(任写一个即可).③当动点P在射线BA的左侧时(如图丁),结论是∠PAC=∠APB+∠PBD.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
