第10周:6.1平行四边形的性质--6.2平行四边形的判定同步测试
文档属性
| 名称 | 第10周:6.1平行四边形的性质--6.2平行四边形的判定同步测试 |

|
|
| 格式 | doc | ||
| 文件大小 | 766.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-03 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
【新北师大版八年级数学(下)周周测】
第10周测试卷
(测试范围:6.1平行四边形的性质--6.2平行四边形的判定)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共30分)
1.□ABCD的对角线交于点O,下列结论错误的是( )
A.△AOB≌△BOC
B.△AOB≌△COD
C.□ABCD是中心对称图形
D.△AOB与△BOC的面积相等
2.已知□ABCD中,∠B=4∠A,则∠D=( )
A.18° B.36° C.72° D.144°
3.ABCD中, ∠A比∠B小200,则∠A的度数为( )
A. 600 B. 800 C. 1000 D. 120021·cn·jy·com
4.在平行四边形ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
A.36° B.108° C.72° D.60°
5.(3分)一个平行四边形的两条对角线的长分别为8和10,则这个平行四边形边长不可能是( )
A.2 B.5 C.8 D.10
6.如图,在□ABCD中,DE平分∠ADC,AD=6,BE=2,则□ABCD的周长是( )
A.16 B.14 C.20 D.24
7.如图,在ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )2·1·c·n·j·y
A.∠E=∠CDF B.EF=DF C.AD=2BF D.BE=2CF
8.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
9.不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD AB ∥CD B.∠A=∠C ∠B=∠D
C.AB=AD BC=CD D.AB=CD AD=BC
10.如图,四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有( )【来源:21cnj*y.co*m】
A.1组 B.2组 C.3组 D.4组
二、填空题:(每小题3分共30分)
11.如图,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是 .【出处:21教育名师】
12.如图,在△ABC中,AB=BC,AB=12 cm,F是AB边上一点,过点F作FE∥BC交AC于点E,过点E作ED∥AB交BC于点D,则四边形BDEF的周长是 .
13.用边长分别为3cm,5cm,7cm的两个全等三角形能拼成 个不同的平行四边形。
14.如图,AB∥DC,AD∥BC,如果∠B =50°,那么∠D= 度.
15.用一根8米长的铜丝围成一个平行四边形,使长边和短边的比是5:3,则长边的长是________米.21教育网
16.如图,在 ABCD中,对角线AC与BD相交于点O,则图中共有 对全等三角形.
17.在 ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE= .21教育名师原创作品
18.如图,在□ABCD中,CE⊥AB于E,如果∠A=125°,那么∠BCE= °.
19.如图, ABCD中,AE⊥BC于E,AF⊥DC于F,若∠B=60°,则∠EAF= .
20.如图,先将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B′,C′在同一直线上,再将折叠的纸片沿EG折叠,使AE落在EF上,则∠AEG= 度.21*cnjy*com
三、解答题:(共40分)
21.(10分)如图,如果□ABCD的内角∠BAD的平分线交BC于点E,且AE=BE,
(1)求□ABCD各内角的度数;(2)若AB=4,AD=5,求□ABCD的面积。
22.(10分)如图,在 ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
23.(10分)如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.21cnjy.com
求证:四边形CDEF是平行四边形.
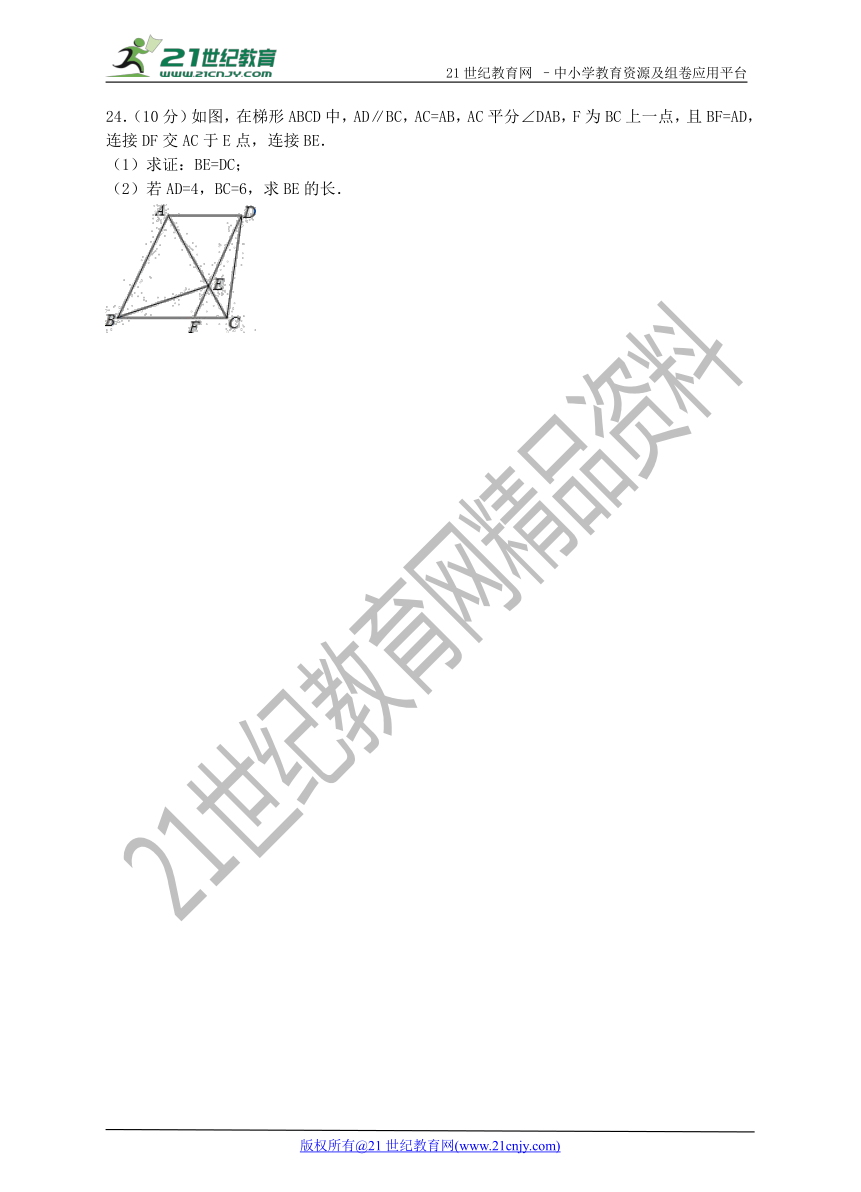
24.(10分)如图,在梯形ABCD中,AD∥BC,AC=AB,AC平分∠DAB,F为BC上一点,且BF=AD,连接DF交AC于E点,连接BE.www.21-cn-jy.com
(1)求证:BE=DC;
(2)若AD=4,BC=6,求BE的长.
参考答案
1.A
【解析】
试题分析:A、△AOB与△BOC不一定全等,故错误.
B、根据平行四边形的对角线互相平分,再结合对顶角相等,得△AOB≌△COD,正确.
C、根据平行四边形的对角线互相平分,故平行四边形是中心对称图形,正确.
D、根据平行四边形的对角线互相平分,再根据三角形的面积计算公式,正确.
故选A.
2.D
【解析】
试题分析:因为在□ABCD中,∠B+∠A=180° ,∠B=∠D,又∠B=4∠A,所以5∠A=180° ,所以∠A=36°,所以∠B=∠D=144°,故选:D.2-1-c-n-j-y
3.B.
【解析】
试题分析:∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠C,
∴∠A+∠B=180°,
∵∠B-∠A =20°,
∴∠B=100°,
∴∠A=80°.
故选B.
4.B.
【解析】
试题分析:在平行四边形ABCD中,根据平行四边形对角相等可得∠A:∠B:∠C:∠D=2:3:2:3,又因平行四边形的内角和是360度,设每份比为x,则得到2x+3x+2x+3x=360°,解得x=36°,即可得∠D=108°.21·世纪*教育网
故答案选B.
5.D
【解析】
试题分析:如图,根据平行四边形的对角线互相平分,由对角线AC=8,BD=10,可得AO=AC=4,BO=DO=BD=5,由三角形三边关系可知:5﹣4<AB<5+4,5﹣4<AD<5+4,求得平行四边形边长的取值范围1<AB<9,1<AD<9,,可求得平行四边形的边长不可能为10.
故选D.
6.C
【解析】
试题分析:根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CE=4的长度,再求出ABCD的周长=2×(AB+AD)=20.【来源:21·世纪·教育·网】
故选C
7.D
【解析】
试题分析:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,
∴∠E=∠CDF, CD∥BE,∠C=∠CBE,所以选项A成立;
又∵BE=AB,∴CD=EB,
在△CDF和△BEF中,,
∴△DCF≌△EBF(AAS),∴EF=DF,所以选项B成立;
∵△DCF≌△EBF,∴CF=BF=BC,∵AD=BC,∴AD=2BF,所以选项C成立;
∵AD≠BE,
∴2CF≠BE,所以选项D不成立;
故选:D.
8.D.
【解析】
试题分析:根据平行四边形的判定定理可得选项A,两条对角线互相平分的四边形是平行四边形,,正确;选项B,两组对边分别相等的四边形是平行四边形,正确;选项C,一组对边平行且相等的四边形是平行四边形,正确;选项D,一组对边相等,另一组对边平行的四边形不一定是平行四边形,例如:等腰梯形,错误;故答案选D.21*cnjy*com
9.C.
【解析】
试题分析:平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.因此,根据平行四边形的判定分别作出判断:【版权所有:21教育】
A.可由(3)判定四边形ABCD为平行四边形;
B.可由(4)判定四边形ABCD为平行四边形;
C.不能由上述5种判定方法判定四边形ABCD为平行四边形;
D.可由(2)判定四边形ABCD为平行四边形
故选C.
10.C
【解析】
试题分析:根据平行四边形的判断定理可作出判断:
①据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,可知①能判断这个四边形是平行四边形;
②根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,可知②能判断这个四边形是平行四边形;
③根据平行四边形的判定定理:两条对角线互相平分的四边形是平行四边形,可知③能判断这个四边形是平行四边形;
④根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,可知④不能判断这个四边形是平行四边形;
故给出下列四组条件中,①②③能判断这个四边形是平行四边形,
故选:C,
11.AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等.
【解析】
试题分析:∵在四边形ABCD中,AB∥CD,∴可添加的条件是:AB=DC,∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)故答案为:AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等.
12.24cm.
【解析】
试题分析:四边形BDEF的周长=2AB=2×12=24cm,∵AB=BC,∴∠A=∠C,∵FE∥BC,∴∠AEF=∠C,∴∠AEF=∠A,∴AF=EF.∵ED∥AB,∴∠A=∠DEC,∴∠DEC=∠C,∴DE=DC,∴四边形BDEF的周长=BF+EF+BD+DE=BF+AF+BD+DC=AB+BC=2AB=24cm.
13.3
【解析】
试题分析:把其中的三边分别重合能够构成三个平行四边形.
14.50°
【解析】
试题分析:根据AB∥CD,∠B=50°可得∠C=180°-50°=130°,根据AD∥BC可得∠C+∠D=180°,则∠D=50°.
15.2.5
【解析】已知长边和短边的比是5:3,设长边和短边长分别为5xm,3xm,根据平行四边形的性质可列方程2(5x+3x)=8,解得x=0.5,所以长边的长是2.5m.
16.4
【解析】
试题分析:可以推出△ABD≌△CDB,△ABC≌△CDA,△AOB≌△COD,△AOD≌△COB.
∵在△ABD和△CDB中,∴△ABD≌△CDB(SSS),∴∠ADB=∠CBD,∠ABD=∠BDC,
∵在△ABC和△CDA中,∴△ABC≌△CDA(SSS),∴∠DAC=∠BCA,∠ACD=∠BAC,
∵在△AOB和△COD中,∴△AOB≌△COD(ASA),∵在△AOD和△COB中
,∴△AOD≌△COB(ASA),
故答案为:4.
17.5
【解析】
试题分析:∵四边形ABCD是平行四变形,∴点O是BD中点,∵点E是边CD的中点,∴OE是△DBC的中位线,∴OE=BC=5.
18.35
【解析】
试题分析:∵四边形平ABCD是平行四边形,
∴AD∥BC,
∴∠B=180°﹣∠A=55°,
又∵CE⊥AB,
∴∠BCE=35°.
19.60°
【解析】
试题分析:根据平行四边形的邻角互补求得∠C,然后在四边形AECF中,利用四边形的内角和定理求解.
解:∵ ABCD中,AB∥CD,
∴∠C=180°﹣∠B=120°,
又∵AE⊥BC于E,AF⊥CD于F,
∴∠AEC=∠AFC=90°,
∴在四边形AECF中,∠EAF=360°﹣∠AEC﹣∠AFC﹣∠C=360°﹣90°﹣90°﹣120°=60°.
故答案是:60°.
20.45.
【解析】
试题分析:利用翻折和平角定义易得组成∠AEF的两个角的和等于平角的一半,得出∠AEF=90°,再利用将折叠的纸片沿EG折叠,使AE落在EF上,得出∠AEG=∠GEA′进而得出答案.
试题解析:根据沿直线折叠的特点,△ABE≌△AB′E,△CEF≌△C′EF,
∴∠AEB=∠AEB′,∠CEF=∠C′EF,
∵∠AEB+∠AEB′+∠CEF+∠C′EF=180°,
∴∠AEB′+∠C′EF=90°,
∵点E,B′,C′在同一直线上,
∴∠AEF=90°,
∵将折叠的纸片沿EG折叠,使AE落在EF上,
∴∠AEG=∠GEA′=∠AEF=45°
21.(1)∠B=∠D=60o,∠BAD=∠C=120o;(2)□ABCD的面积是
【解析】
试题分析:由平行四边形ABCD中,∠BAD的平分线交BC于E,易得∠BAE=∠BEA,则AB=BE;又因为AE=BE,所以△ABE是等边三角形;即能求得∠BCD的度数.然后过A作AF⊥BC于F,然后根据勾股定理求得AF的长,然后求出平行四边形的面积.
试题解析:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
∵AE=BE
∴△ABE是等边三角形
∴∠B=60°
∴∠BCD=120°
∴□ABCD各内角的度数分别是:∠B=∠D=60°,∠BAD=∠C=120°.
过A作AF⊥BC于F,
∵AB=4,∠B=60°
∴BF=2
∴AF=
∴平行四边形的面积=5×=10
22.详见解析.
【解析】
试题分析:(1)根据全等三角形的判定方法,判断出△ADE≌△CBF,即可推得DE=BF.(2)首先判断出DE∥BF;然后根据一组对边平行且相等的四边形是平行四边形,推得四边形DEBF是平行四边形即可.21世纪教育网版权所有
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
∴△ADE≌△CBF,
∴DE=BF.
(2)由(1),可得∴△ADE≌△CBF,
∴∠ADE=∠CBF,
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE,
∴DE∥BF,
又∵DE=BF,
∴四边形DEBF是平行四边形.
23.证明见解析
【解析】
试题分析:首先证明△AEF≌△BCD可得CD=EF,∠EFD=∠CDB,进而可证明ED∥CF,根据一组对边平行且相等的四边形是平行四边形可得结论.www-2-1-cnjy-com
试题解析:∵BC∥AE,∴∠A=∠B,∵FB=AD,
∴FB+DF=AD+DF,
∴AF=BD,
在△AEF和△BCD中,
,
∴△AEF≌△BCD(SAS),
∴CD=EF,∠EFD=∠CDB,
∴CD∥EF,
∴四边形CDEF是平行四边形.
24.(1)见解析 (2)2
【解析】(1)证明:∵AC平分∠DAB,
∴∠DAC=∠BAC.
∵AD∥BC,∠DAC=∠ACB
∴∠BAC=∠ACB,
∴AB=BC,
∵AC=AB,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠DAC=∠ACB=∠ACB=60°,
∵AD∥BC,AD=BF,
∴四边形ABFD是平行四边形,
∴DF∥AB,
∴∠CEF=∠AED=60°,
∴△CEF、△ADE都是等边三角形,
∴∠BFE=∠CED,EF=EC,DE=AD=BF,
∴△BFE≌△DEC,
∴BE=DC
(2)解:∵四边形ABFD是平行四边形,
∴DF=AB,BF=DE=AD
∵△ABC是等边三角形,
∴BC=AB=DF=6
作EG⊥BC于点G,
则由勾股定理得:EG==,
∴在Rt△BEG中,
BE===2.
(1)分别证明△ABC、△CEF、△ADE都是等边三角形,然后证得△BFE≌△DEC,从而证得BE=DC;
(2)利用上题证得的平行四边形和等边三角形利用勾股定理求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
【新北师大版八年级数学(下)周周测】
第10周测试卷
(测试范围:6.1平行四边形的性质--6.2平行四边形的判定)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共30分)
1.□ABCD的对角线交于点O,下列结论错误的是( )
A.△AOB≌△BOC
B.△AOB≌△COD
C.□ABCD是中心对称图形
D.△AOB与△BOC的面积相等
2.已知□ABCD中,∠B=4∠A,则∠D=( )
A.18° B.36° C.72° D.144°
3.ABCD中, ∠A比∠B小200,则∠A的度数为( )
A. 600 B. 800 C. 1000 D. 120021·cn·jy·com
4.在平行四边形ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
A.36° B.108° C.72° D.60°
5.(3分)一个平行四边形的两条对角线的长分别为8和10,则这个平行四边形边长不可能是( )
A.2 B.5 C.8 D.10
6.如图,在□ABCD中,DE平分∠ADC,AD=6,BE=2,则□ABCD的周长是( )
A.16 B.14 C.20 D.24
7.如图,在ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )2·1·c·n·j·y
A.∠E=∠CDF B.EF=DF C.AD=2BF D.BE=2CF
8.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
9.不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD AB ∥CD B.∠A=∠C ∠B=∠D
C.AB=AD BC=CD D.AB=CD AD=BC
10.如图,四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判断这个四边形是平行四边形的条件共有( )【来源:21cnj*y.co*m】
A.1组 B.2组 C.3组 D.4组
二、填空题:(每小题3分共30分)
11.如图,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是 .【出处:21教育名师】
12.如图,在△ABC中,AB=BC,AB=12 cm,F是AB边上一点,过点F作FE∥BC交AC于点E,过点E作ED∥AB交BC于点D,则四边形BDEF的周长是 .
13.用边长分别为3cm,5cm,7cm的两个全等三角形能拼成 个不同的平行四边形。
14.如图,AB∥DC,AD∥BC,如果∠B =50°,那么∠D= 度.
15.用一根8米长的铜丝围成一个平行四边形,使长边和短边的比是5:3,则长边的长是________米.21教育网
16.如图,在 ABCD中,对角线AC与BD相交于点O,则图中共有 对全等三角形.
17.在 ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE= .21教育名师原创作品
18.如图,在□ABCD中,CE⊥AB于E,如果∠A=125°,那么∠BCE= °.
19.如图, ABCD中,AE⊥BC于E,AF⊥DC于F,若∠B=60°,则∠EAF= .
20.如图,先将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B′,C′在同一直线上,再将折叠的纸片沿EG折叠,使AE落在EF上,则∠AEG= 度.21*cnjy*com
三、解答题:(共40分)
21.(10分)如图,如果□ABCD的内角∠BAD的平分线交BC于点E,且AE=BE,
(1)求□ABCD各内角的度数;(2)若AB=4,AD=5,求□ABCD的面积。
22.(10分)如图,在 ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
23.(10分)如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.21cnjy.com
求证:四边形CDEF是平行四边形.
24.(10分)如图,在梯形ABCD中,AD∥BC,AC=AB,AC平分∠DAB,F为BC上一点,且BF=AD,连接DF交AC于E点,连接BE.www.21-cn-jy.com
(1)求证:BE=DC;
(2)若AD=4,BC=6,求BE的长.
参考答案
1.A
【解析】
试题分析:A、△AOB与△BOC不一定全等,故错误.
B、根据平行四边形的对角线互相平分,再结合对顶角相等,得△AOB≌△COD,正确.
C、根据平行四边形的对角线互相平分,故平行四边形是中心对称图形,正确.
D、根据平行四边形的对角线互相平分,再根据三角形的面积计算公式,正确.
故选A.
2.D
【解析】
试题分析:因为在□ABCD中,∠B+∠A=180° ,∠B=∠D,又∠B=4∠A,所以5∠A=180° ,所以∠A=36°,所以∠B=∠D=144°,故选:D.2-1-c-n-j-y
3.B.
【解析】
试题分析:∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠C,
∴∠A+∠B=180°,
∵∠B-∠A =20°,
∴∠B=100°,
∴∠A=80°.
故选B.
4.B.
【解析】
试题分析:在平行四边形ABCD中,根据平行四边形对角相等可得∠A:∠B:∠C:∠D=2:3:2:3,又因平行四边形的内角和是360度,设每份比为x,则得到2x+3x+2x+3x=360°,解得x=36°,即可得∠D=108°.21·世纪*教育网
故答案选B.
5.D
【解析】
试题分析:如图,根据平行四边形的对角线互相平分,由对角线AC=8,BD=10,可得AO=AC=4,BO=DO=BD=5,由三角形三边关系可知:5﹣4<AB<5+4,5﹣4<AD<5+4,求得平行四边形边长的取值范围1<AB<9,1<AD<9,,可求得平行四边形的边长不可能为10.
故选D.
6.C
【解析】
试题分析:根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CE=4的长度,再求出ABCD的周长=2×(AB+AD)=20.【来源:21·世纪·教育·网】
故选C
7.D
【解析】
试题分析:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,
∴∠E=∠CDF, CD∥BE,∠C=∠CBE,所以选项A成立;
又∵BE=AB,∴CD=EB,
在△CDF和△BEF中,,
∴△DCF≌△EBF(AAS),∴EF=DF,所以选项B成立;
∵△DCF≌△EBF,∴CF=BF=BC,∵AD=BC,∴AD=2BF,所以选项C成立;
∵AD≠BE,
∴2CF≠BE,所以选项D不成立;
故选:D.
8.D.
【解析】
试题分析:根据平行四边形的判定定理可得选项A,两条对角线互相平分的四边形是平行四边形,,正确;选项B,两组对边分别相等的四边形是平行四边形,正确;选项C,一组对边平行且相等的四边形是平行四边形,正确;选项D,一组对边相等,另一组对边平行的四边形不一定是平行四边形,例如:等腰梯形,错误;故答案选D.21*cnjy*com
9.C.
【解析】
试题分析:平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.因此,根据平行四边形的判定分别作出判断:【版权所有:21教育】
A.可由(3)判定四边形ABCD为平行四边形;
B.可由(4)判定四边形ABCD为平行四边形;
C.不能由上述5种判定方法判定四边形ABCD为平行四边形;
D.可由(2)判定四边形ABCD为平行四边形
故选C.
10.C
【解析】
试题分析:根据平行四边形的判断定理可作出判断:
①据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,可知①能判断这个四边形是平行四边形;
②根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,可知②能判断这个四边形是平行四边形;
③根据平行四边形的判定定理:两条对角线互相平分的四边形是平行四边形,可知③能判断这个四边形是平行四边形;
④根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,可知④不能判断这个四边形是平行四边形;
故给出下列四组条件中,①②③能判断这个四边形是平行四边形,
故选:C,
11.AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等.
【解析】
试题分析:∵在四边形ABCD中,AB∥CD,∴可添加的条件是:AB=DC,∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)故答案为:AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等.
12.24cm.
【解析】
试题分析:四边形BDEF的周长=2AB=2×12=24cm,∵AB=BC,∴∠A=∠C,∵FE∥BC,∴∠AEF=∠C,∴∠AEF=∠A,∴AF=EF.∵ED∥AB,∴∠A=∠DEC,∴∠DEC=∠C,∴DE=DC,∴四边形BDEF的周长=BF+EF+BD+DE=BF+AF+BD+DC=AB+BC=2AB=24cm.
13.3
【解析】
试题分析:把其中的三边分别重合能够构成三个平行四边形.
14.50°
【解析】
试题分析:根据AB∥CD,∠B=50°可得∠C=180°-50°=130°,根据AD∥BC可得∠C+∠D=180°,则∠D=50°.
15.2.5
【解析】已知长边和短边的比是5:3,设长边和短边长分别为5xm,3xm,根据平行四边形的性质可列方程2(5x+3x)=8,解得x=0.5,所以长边的长是2.5m.
16.4
【解析】
试题分析:可以推出△ABD≌△CDB,△ABC≌△CDA,△AOB≌△COD,△AOD≌△COB.
∵在△ABD和△CDB中,∴△ABD≌△CDB(SSS),∴∠ADB=∠CBD,∠ABD=∠BDC,
∵在△ABC和△CDA中,∴△ABC≌△CDA(SSS),∴∠DAC=∠BCA,∠ACD=∠BAC,
∵在△AOB和△COD中,∴△AOB≌△COD(ASA),∵在△AOD和△COB中
,∴△AOD≌△COB(ASA),
故答案为:4.
17.5
【解析】
试题分析:∵四边形ABCD是平行四变形,∴点O是BD中点,∵点E是边CD的中点,∴OE是△DBC的中位线,∴OE=BC=5.
18.35
【解析】
试题分析:∵四边形平ABCD是平行四边形,
∴AD∥BC,
∴∠B=180°﹣∠A=55°,
又∵CE⊥AB,
∴∠BCE=35°.
19.60°
【解析】
试题分析:根据平行四边形的邻角互补求得∠C,然后在四边形AECF中,利用四边形的内角和定理求解.
解:∵ ABCD中,AB∥CD,
∴∠C=180°﹣∠B=120°,
又∵AE⊥BC于E,AF⊥CD于F,
∴∠AEC=∠AFC=90°,
∴在四边形AECF中,∠EAF=360°﹣∠AEC﹣∠AFC﹣∠C=360°﹣90°﹣90°﹣120°=60°.
故答案是:60°.
20.45.
【解析】
试题分析:利用翻折和平角定义易得组成∠AEF的两个角的和等于平角的一半,得出∠AEF=90°,再利用将折叠的纸片沿EG折叠,使AE落在EF上,得出∠AEG=∠GEA′进而得出答案.
试题解析:根据沿直线折叠的特点,△ABE≌△AB′E,△CEF≌△C′EF,
∴∠AEB=∠AEB′,∠CEF=∠C′EF,
∵∠AEB+∠AEB′+∠CEF+∠C′EF=180°,
∴∠AEB′+∠C′EF=90°,
∵点E,B′,C′在同一直线上,
∴∠AEF=90°,
∵将折叠的纸片沿EG折叠,使AE落在EF上,
∴∠AEG=∠GEA′=∠AEF=45°
21.(1)∠B=∠D=60o,∠BAD=∠C=120o;(2)□ABCD的面积是
【解析】
试题分析:由平行四边形ABCD中,∠BAD的平分线交BC于E,易得∠BAE=∠BEA,则AB=BE;又因为AE=BE,所以△ABE是等边三角形;即能求得∠BCD的度数.然后过A作AF⊥BC于F,然后根据勾股定理求得AF的长,然后求出平行四边形的面积.
试题解析:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
∵AE=BE
∴△ABE是等边三角形
∴∠B=60°
∴∠BCD=120°
∴□ABCD各内角的度数分别是:∠B=∠D=60°,∠BAD=∠C=120°.
过A作AF⊥BC于F,
∵AB=4,∠B=60°
∴BF=2
∴AF=
∴平行四边形的面积=5×=10
22.详见解析.
【解析】
试题分析:(1)根据全等三角形的判定方法,判断出△ADE≌△CBF,即可推得DE=BF.(2)首先判断出DE∥BF;然后根据一组对边平行且相等的四边形是平行四边形,推得四边形DEBF是平行四边形即可.21世纪教育网版权所有
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
∴△ADE≌△CBF,
∴DE=BF.
(2)由(1),可得∴△ADE≌△CBF,
∴∠ADE=∠CBF,
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE,
∴DE∥BF,
又∵DE=BF,
∴四边形DEBF是平行四边形.
23.证明见解析
【解析】
试题分析:首先证明△AEF≌△BCD可得CD=EF,∠EFD=∠CDB,进而可证明ED∥CF,根据一组对边平行且相等的四边形是平行四边形可得结论.www-2-1-cnjy-com
试题解析:∵BC∥AE,∴∠A=∠B,∵FB=AD,
∴FB+DF=AD+DF,
∴AF=BD,
在△AEF和△BCD中,
,
∴△AEF≌△BCD(SAS),
∴CD=EF,∠EFD=∠CDB,
∴CD∥EF,
∴四边形CDEF是平行四边形.
24.(1)见解析 (2)2
【解析】(1)证明:∵AC平分∠DAB,
∴∠DAC=∠BAC.
∵AD∥BC,∠DAC=∠ACB
∴∠BAC=∠ACB,
∴AB=BC,
∵AC=AB,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠DAC=∠ACB=∠ACB=60°,
∵AD∥BC,AD=BF,
∴四边形ABFD是平行四边形,
∴DF∥AB,
∴∠CEF=∠AED=60°,
∴△CEF、△ADE都是等边三角形,
∴∠BFE=∠CED,EF=EC,DE=AD=BF,
∴△BFE≌△DEC,
∴BE=DC
(2)解:∵四边形ABFD是平行四边形,
∴DF=AB,BF=DE=AD
∵△ABC是等边三角形,
∴BC=AB=DF=6
作EG⊥BC于点G,
则由勾股定理得:EG==,
∴在Rt△BEG中,
BE===2.
(1)分别证明△ABC、△CEF、△ADE都是等边三角形,然后证得△BFE≌△DEC,从而证得BE=DC;
(2)利用上题证得的平行四边形和等边三角形利用勾股定理求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
