苏科版八年级数学下册第十一章反比例函数 测试卷(含答案)
文档属性
| 名称 | 苏科版八年级数学下册第十一章反比例函数 测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 166.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-10 18:09:58 | ||
图片预览

文档简介
第十一章
反比例函数
测试卷
(总分100分
时间40分钟)
一、选择题(每小题3分,共24分)
1.下列各点中,在反比例函数y=图象上的是
(
)
A.(-1,8)
B.(-2,4)
C.(1,7)
D.(2,4)
2.已知点A(2,3)在反比例函数y=的图象上,则k的值是
(
)
A.-7
B.7
C.-5
D.5
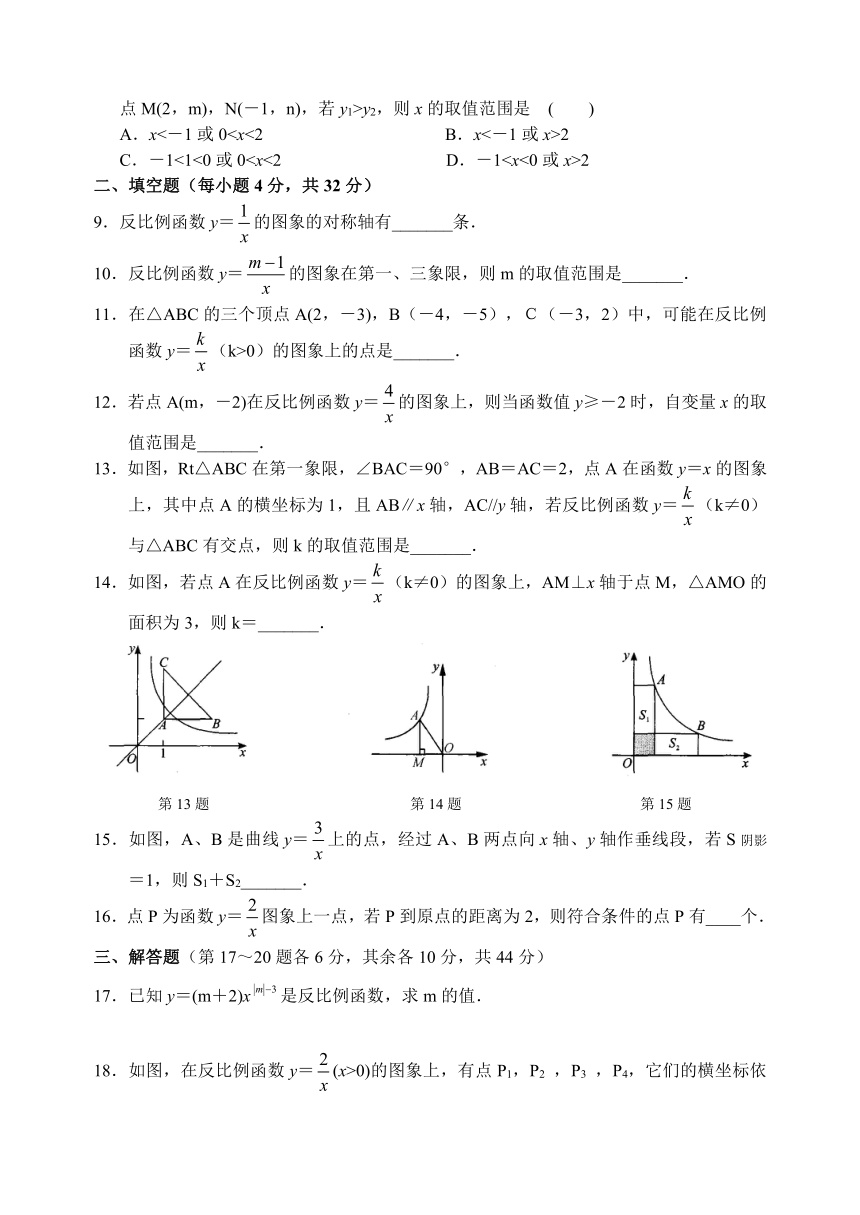
3.直角三角形两直角边的长分别为x,y,它的面积为3,则y与x之间的函数关系用图象表示大致是
(
)
4.反比例函数的图象在每个象限内y随x的增大而减小,则k的值可为(
)
A.-1
B.0
C.1
D.2
5.函数y=a(x-3)与y=在同一坐标系中的大致图象是
(
)
6.已知点A(x1,y1),B(x2,y2)是反比例函数y=的图象上的两点,若x1<0(
)
A.
y1<0B.y2<0C.y1D.y27.如图,A、C是函数y=的图象上任意两点,过点A作y轴的垂线,
垂足为,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,
Rt△COD的面积为S2,则S1和S2的大小关系是
(
)
A.S1>S2
B.S1C.S1=S2
D.不能确定
8.如图,函数y1=x-1和函数y2=的图象相交于
点M(2,m),N(-1,n),若y1>y2,则x的取值范围是
(
)
A.x<-1或0B.x<-1或x>2
C.-1<1<0或0D.-12
二、填空题(每小题4分,共32分)
9.反比例函数y=的图象的对称轴有_______条.
10.反比例函数y=的图象在第一、三象限,则m的取值范围是_______.
11.在△ABC的三个顶点A(2,-3),B(-4,-5),C(-3,2)中,可能在反比例函数y=(k>0)的图象上的点是_______.
12.若点A(m,-2)在反比例函数y=的图象上,则当函数值y≥-2时,自变量x的取值范围是_______.
13.如图,Rt△ABC在第一象限,∠BAC=90°,AB=AC=2,点A在函数y=x的图象上,其中点A的横坐标为1,且AB∥x轴,AC//y轴,若反比例函数y=(k≠0)与△ABC有交点,则k的取值范围是_______.
14.如图,若点A在反比例函数y=(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k=_______.
第13题
第14题
第15题
15.如图,A、B是曲线y=上的点,经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2_______.
16.点P为函数y=图象上一点,若P到原点的距离为2,则符合条件的点P有____个.
三、解答题(第17~20题各6分,其余各10分,共44分)
17.已知y=(m+2)x是反比例函数,求m的值.
18.如图,在反比例函数y=(x>0)的图象上,有点P1,P2
,P3
,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,求S1,S2,S3的和.
19.如图,矩形ABCD中,AB=6,AD=8,点P在BC边上移动(不与点B、C重合),设PA=x,点D到PA的距离DE=y.
(1)求y与x之间的函数关系式及自变量x的取值范围.
(2)画出函数图象.
20.如图,过y轴上点A的一次函数与反比例函数相交于B、D两点,B(-2,3),过B作BC⊥x轴于C,四边形OABC面积为4.
(1)求反比例函数和一次函数的关系式;
(2)求点D的坐标;
(3)当x在什么取值范围内,一次函数的值大于反比例函数的值.(直接写出结果)
21.用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系.寄宿生小红、小敏晚饭后用同一种洗衣粉各自洗一件同样的衣服,漂洗时,小红每次用水(约10升),小敏每次用半盆水(约5升).如果她们都用了5克洗衣粉,第一次漂洗后,小红的衣服中残留的洗衣粉还有1.5克,小敏的衣服中残留的洗衣粉还有2克.
(1)请帮助小红、小敏求出各自衣服中洗衣粉的残留量y与漂洗次数x的函数关系式;
(2)当洗衣粉的残留量降至0.5克时,便视为衣服漂洗干净,从节约用水的角度来看,你认为谁的漂洗方法值得提倡,为什么?
22.如图,一次函数y=k1x+b与反比例函数y=的图象交于A(1,6),B(b,3)两点.
(1)求k1、k2的值,
(2)直接写出k1x+b->0时x的取值范围;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P.当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.
参考答案
1.D
2.D
3.C
4.D
5.D
6.A
7.C
8.D
9.2
10.m>1
11.点
B 12.x≤-2或x>0
13.
1≤k≤4
14.-6
15.
4
16.
2
17.m=2. 18.1.5 19.y=(6(3)x<-2或0(x为正整数). (2)小红共用水30升,小敏共用水20升,小敏的方法更值得提倡.
22.(1) (2)1
反比例函数
测试卷
(总分100分
时间40分钟)
一、选择题(每小题3分,共24分)
1.下列各点中,在反比例函数y=图象上的是
(
)
A.(-1,8)
B.(-2,4)
C.(1,7)
D.(2,4)
2.已知点A(2,3)在反比例函数y=的图象上,则k的值是
(
)
A.-7
B.7
C.-5
D.5
3.直角三角形两直角边的长分别为x,y,它的面积为3,则y与x之间的函数关系用图象表示大致是
(
)
4.反比例函数的图象在每个象限内y随x的增大而减小,则k的值可为(
)
A.-1
B.0
C.1
D.2
5.函数y=a(x-3)与y=在同一坐标系中的大致图象是
(
)
6.已知点A(x1,y1),B(x2,y2)是反比例函数y=的图象上的两点,若x1<0
)
A.
y1<0
垂足为,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,
Rt△COD的面积为S2,则S1和S2的大小关系是
(
)
A.S1>S2
B.S1
D.不能确定
8.如图,函数y1=x-1和函数y2=的图象相交于
点M(2,m),N(-1,n),若y1>y2,则x的取值范围是
(
)
A.x<-1或0
C.-1<1<0或0
二、填空题(每小题4分,共32分)
9.反比例函数y=的图象的对称轴有_______条.
10.反比例函数y=的图象在第一、三象限,则m的取值范围是_______.
11.在△ABC的三个顶点A(2,-3),B(-4,-5),C(-3,2)中,可能在反比例函数y=(k>0)的图象上的点是_______.
12.若点A(m,-2)在反比例函数y=的图象上,则当函数值y≥-2时,自变量x的取值范围是_______.
13.如图,Rt△ABC在第一象限,∠BAC=90°,AB=AC=2,点A在函数y=x的图象上,其中点A的横坐标为1,且AB∥x轴,AC//y轴,若反比例函数y=(k≠0)与△ABC有交点,则k的取值范围是_______.
14.如图,若点A在反比例函数y=(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为3,则k=_______.
第13题
第14题
第15题
15.如图,A、B是曲线y=上的点,经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2_______.
16.点P为函数y=图象上一点,若P到原点的距离为2,则符合条件的点P有____个.
三、解答题(第17~20题各6分,其余各10分,共44分)
17.已知y=(m+2)x是反比例函数,求m的值.
18.如图,在反比例函数y=(x>0)的图象上,有点P1,P2
,P3
,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,求S1,S2,S3的和.
19.如图,矩形ABCD中,AB=6,AD=8,点P在BC边上移动(不与点B、C重合),设PA=x,点D到PA的距离DE=y.
(1)求y与x之间的函数关系式及自变量x的取值范围.
(2)画出函数图象.
20.如图,过y轴上点A的一次函数与反比例函数相交于B、D两点,B(-2,3),过B作BC⊥x轴于C,四边形OABC面积为4.
(1)求反比例函数和一次函数的关系式;
(2)求点D的坐标;
(3)当x在什么取值范围内,一次函数的值大于反比例函数的值.(直接写出结果)
21.用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系.寄宿生小红、小敏晚饭后用同一种洗衣粉各自洗一件同样的衣服,漂洗时,小红每次用水(约10升),小敏每次用半盆水(约5升).如果她们都用了5克洗衣粉,第一次漂洗后,小红的衣服中残留的洗衣粉还有1.5克,小敏的衣服中残留的洗衣粉还有2克.
(1)请帮助小红、小敏求出各自衣服中洗衣粉的残留量y与漂洗次数x的函数关系式;
(2)当洗衣粉的残留量降至0.5克时,便视为衣服漂洗干净,从节约用水的角度来看,你认为谁的漂洗方法值得提倡,为什么?
22.如图,一次函数y=k1x+b与反比例函数y=的图象交于A(1,6),B(b,3)两点.
(1)求k1、k2的值,
(2)直接写出k1x+b->0时x的取值范围;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P.当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.
参考答案
1.D
2.D
3.C
4.D
5.D
6.A
7.C
8.D
9.2
10.m>1
11.点
B 12.x≤-2或x>0
13.
1≤k≤4
14.-6
15.
4
16.
2
17.m=2. 18.1.5 19.y=(6
22.(1) (2)1
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
