18.2.3正方形 课件
图片预览


文档简介
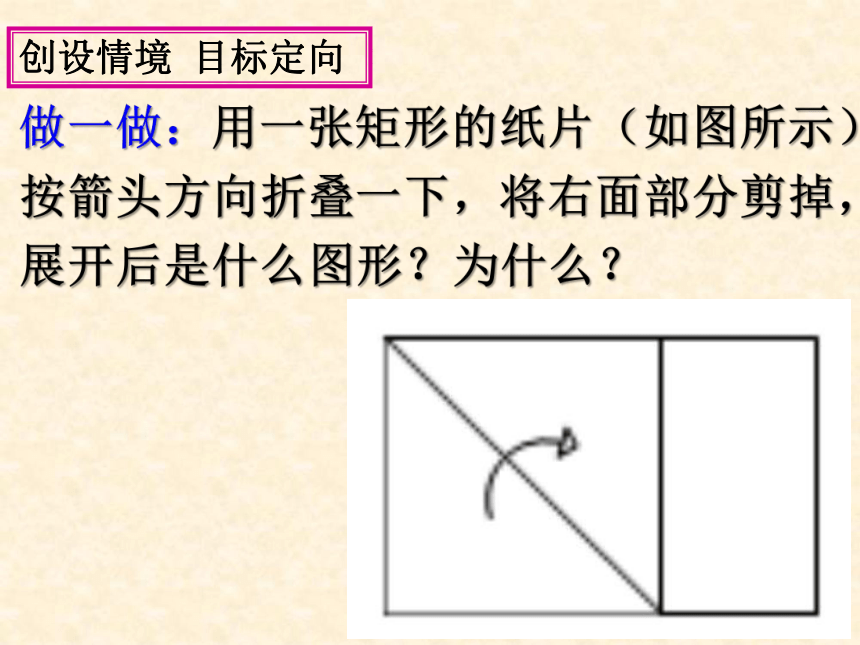
课件14张PPT。创设情境 目标定向 做一做:用一张矩形的纸片(如图所示)按箭头方向折叠一下,将右面部分剪掉,展开后是什么图形?为什么?18.2.3 正方形人教版八年级数学下册18.2特殊的平行四边形 1.理解正方形与平行四边形、矩形、菱形概念之间的联系和区别;
2.能用正方形的定义、性质和判定进行推理与计算.
学习重点
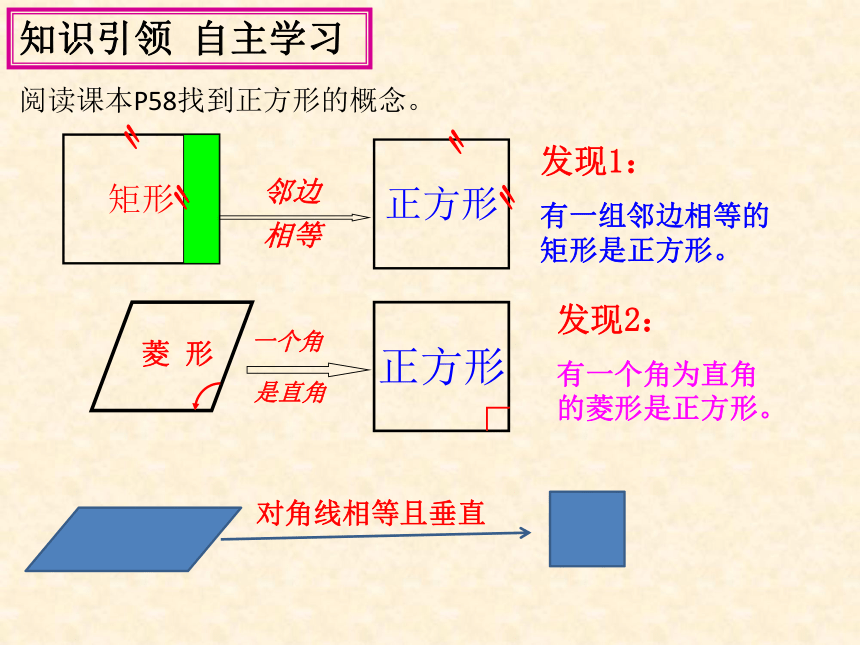
正方形与平行四边形、矩形、菱形的联系.学习目标矩形〃〃正方形邻边相等〃〃发现1:
有一组邻边相等的矩形是正方形。一个角是直角正方形∟发现2:
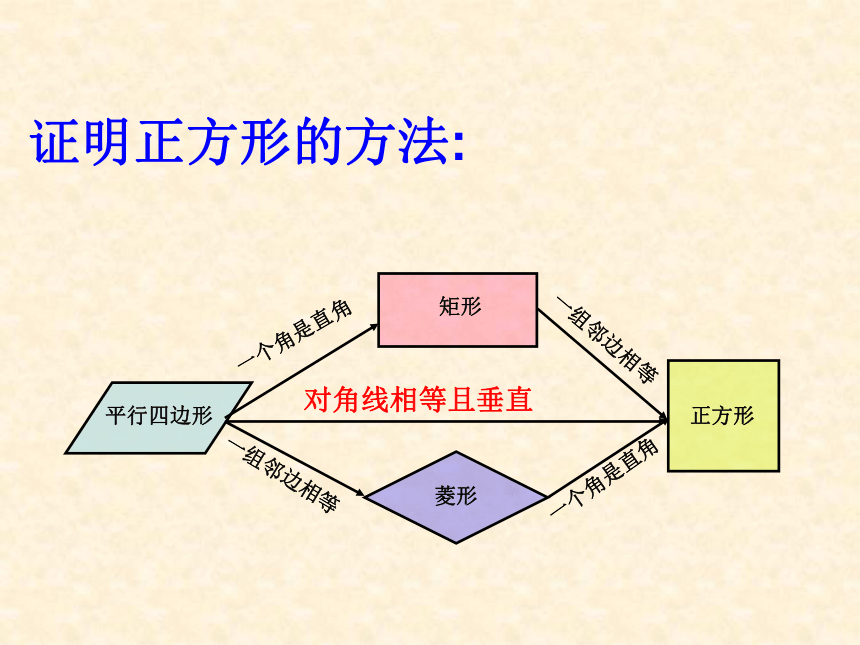
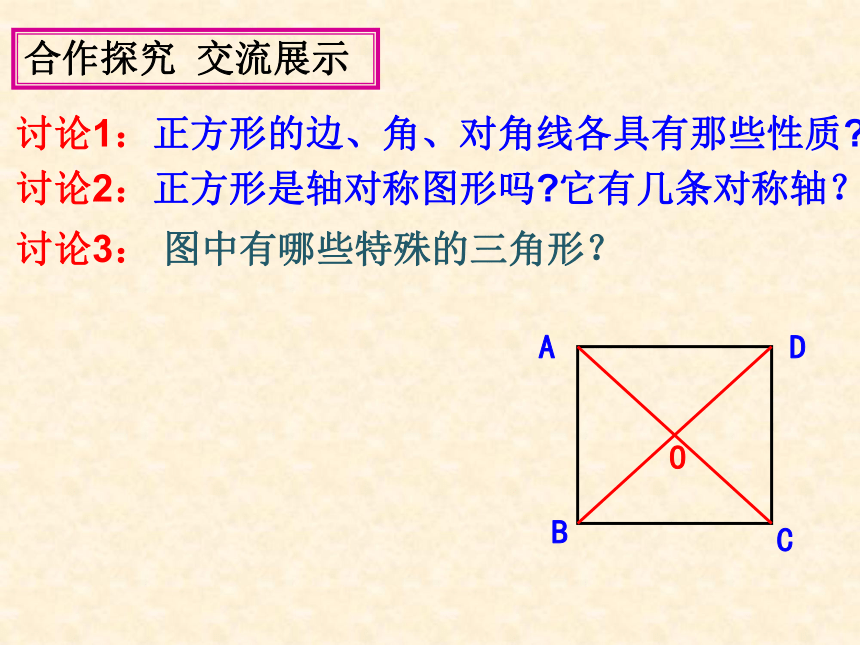
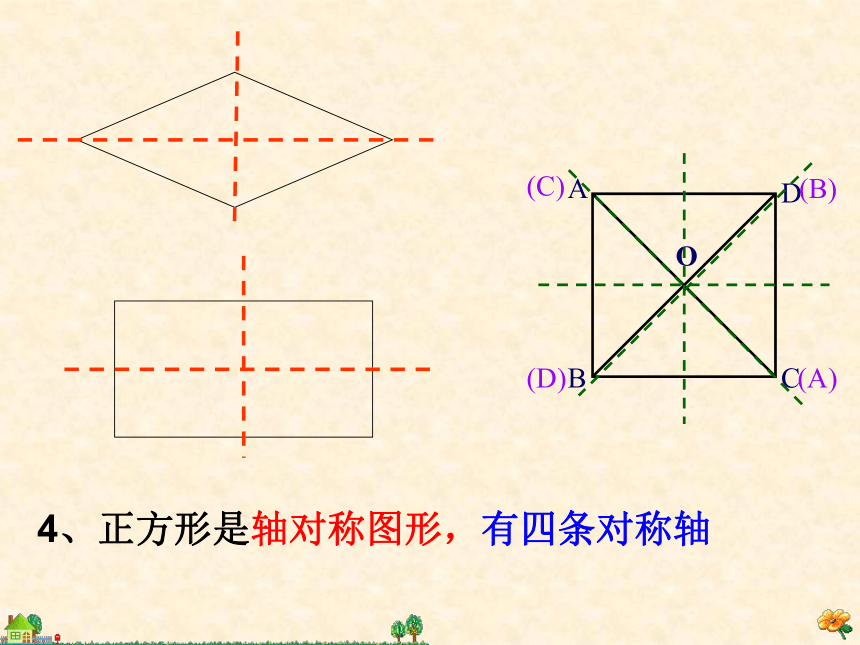
有一个角为直角的菱形是正方形。对角线相等且垂直知识引领 自主学习 阅读课本P58找到正方形的概念。证明正方形的方法: 一个角是直角 一组邻边相等 一组邻边相等 一个角是直角 对角线相等且垂直讨论1:正方形的边、角、对角线各具有那些性质?讨论2:正方形是轴对称图形吗?它有几条对称轴?讨论3: 图中有哪些特殊的三角形?合作探究 交流展示 (A)(B)(C)(D)4、正方形是轴对称图形,有四条对称轴正方形的性质归纳:对边平行,四条边都相等。四个角都是直角1 对角线互相垂直平分且相等2 每一条对角线平分每一组对角轴对称图形,有4条对称轴有8个等腰直角三角形启发引导 精讲点拨 四边形
平行四边形
矩形
菱形
正方形完成下图:1、正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分
C、对角互补.
D、对角线相等.2、正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD系列训练 当堂达标 436245、如图,已知正方形ABCD,以AB为边向正方形外作等边三角形ABE,连结DE,CE,
则∠DEC= 度。306、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,猜想AE与CG的位置
关系,并证明你的猜想。(1)证△ADE≌△CDG(SAS)(2)AE⊥CG(1)本节课学习了哪些内容?
(2)正方形与平行四边形、矩形、菱形之间有什么联
系与区别?它有什么性质?怎样判定?
(3)回忆从平行四边形到矩形、菱形再到正方形的学
习过程,我们研究这些图形的次序是什么?其中
体现了什么思想?课堂小结 回扣目标 作业:教科书第61页习题第7,13,15题. 课后作业
2.能用正方形的定义、性质和判定进行推理与计算.
学习重点
正方形与平行四边形、矩形、菱形的联系.学习目标矩形〃〃正方形邻边相等〃〃发现1:
有一组邻边相等的矩形是正方形。一个角是直角正方形∟发现2:
有一个角为直角的菱形是正方形。对角线相等且垂直知识引领 自主学习 阅读课本P58找到正方形的概念。证明正方形的方法: 一个角是直角 一组邻边相等 一组邻边相等 一个角是直角 对角线相等且垂直讨论1:正方形的边、角、对角线各具有那些性质?讨论2:正方形是轴对称图形吗?它有几条对称轴?讨论3: 图中有哪些特殊的三角形?合作探究 交流展示 (A)(B)(C)(D)4、正方形是轴对称图形,有四条对称轴正方形的性质归纳:对边平行,四条边都相等。四个角都是直角1 对角线互相垂直平分且相等2 每一条对角线平分每一组对角轴对称图形,有4条对称轴有8个等腰直角三角形启发引导 精讲点拨 四边形
平行四边形
矩形
菱形
正方形完成下图:1、正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分
C、对角互补.
D、对角线相等.2、正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD系列训练 当堂达标 436245、如图,已知正方形ABCD,以AB为边向正方形外作等边三角形ABE,连结DE,CE,
则∠DEC= 度。306、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,猜想AE与CG的位置
关系,并证明你的猜想。(1)证△ADE≌△CDG(SAS)(2)AE⊥CG(1)本节课学习了哪些内容?
(2)正方形与平行四边形、矩形、菱形之间有什么联
系与区别?它有什么性质?怎样判定?
(3)回忆从平行四边形到矩形、菱形再到正方形的学
习过程,我们研究这些图形的次序是什么?其中
体现了什么思想?课堂小结 回扣目标 作业:教科书第61页习题第7,13,15题. 课后作业
