2016—2017北师大版数学七年级下册第五章生活中的轴对称 单元检测题(含答案)
文档属性
| 名称 | 2016—2017北师大版数学七年级下册第五章生活中的轴对称 单元检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 586.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-11 19:06:47 | ||
图片预览

文档简介
第五章生活中的轴对称
单元检测题
时间:
分钟
满分:120分
班级:
姓名:
得分:
一、选择题(每小题4分,共32分)
1.图1所示的图形中,轴对称图形有(
)
A.4个
B.3个
C.2个
D.1个
图1
2.下列说法中错误的是(
)
A.两个关于某直线对称的图形一定能够完全重合
B.成轴对称的两个图形,其对应点的连线的垂直平分线是它们的对称轴
C.对称图形的对称点一定在对称轴的两侧
D.平面上两个能够完全重合的图形不一定关于某直线对称
3.下列分子结构模型平面图中,只有一条对称轴的是(
)
4.下列说法中,正确的是(
)
A.等腰三角形底边上的中线就是底边的垂直平分线
B.等腰三角形的对称轴是底边上的高
C.一条线段可看做是以它的垂直平分线为对称轴的轴对称图形
D.等腰三角形的对称轴就是顶角平分线
5.如图2,△ABC中,AB=AC,∠B=70°,则∠C的度数是( )
A.
40°
B.
50°
C.
55°
D.
70°
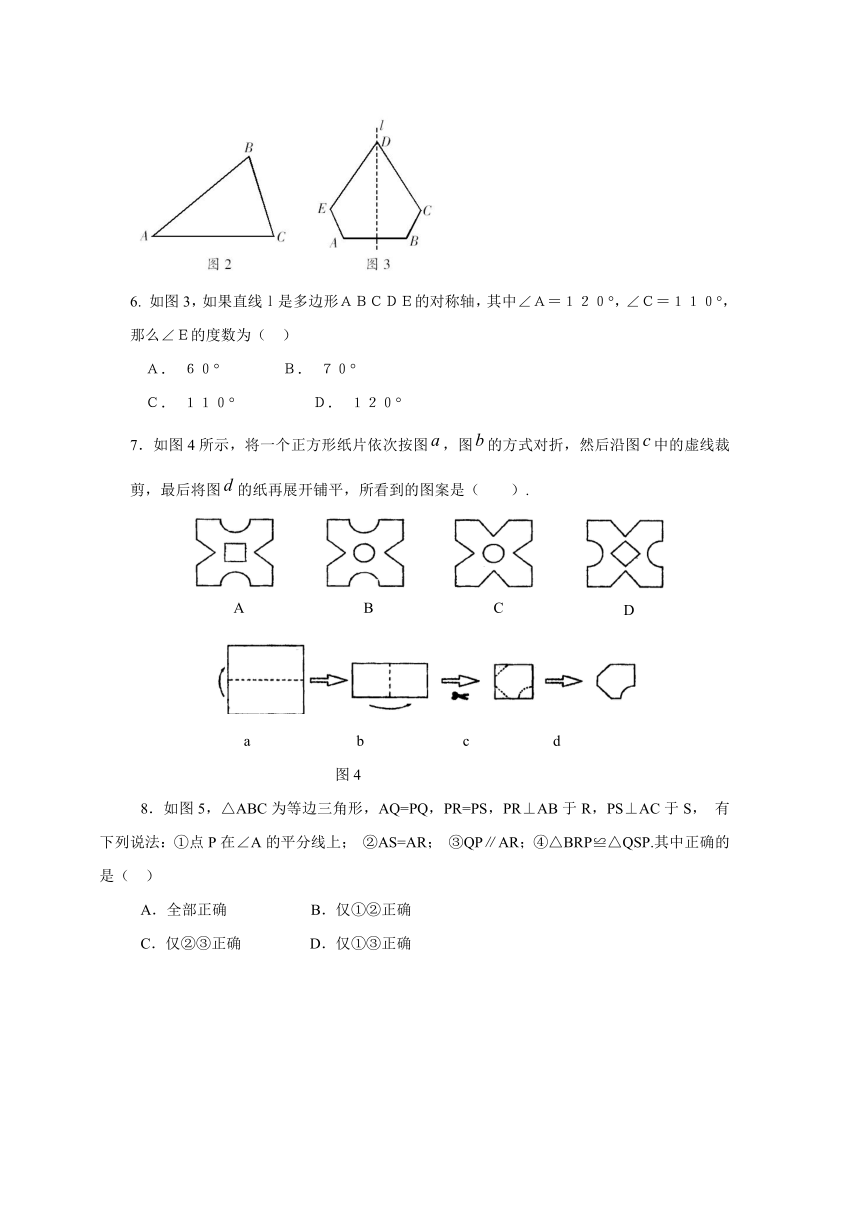
6.
如图3,如果直线l是多边形ABCDE的对称轴,其中∠A=120°,∠C=110°,那么∠E的度数为(
)
A.
60°
B.
70°
C.
110°
D.
120°
7.如图4所示,将一个正方形纸片依次按图,图的方式对折,然后沿图中的虚线裁剪,最后将图的纸再展开铺平,所看到的图案是(
).
a
b
c
d
图4
8.如图5,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,有下列说法:①点P在∠A的平分线上;
②AS=AR;
③QP∥AR;④△BRP≌△QSP.其中正确的是(
)
A.全部正确
B.仅①②正确
C.仅②③正确
D.仅①③正确
二、填空题(每小题4分,共32分)
9.如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做
,这条直线叫做
.
10.
一路发的谐音可以用数字“168”表示,其中数字
可以看做是轴对称图形.
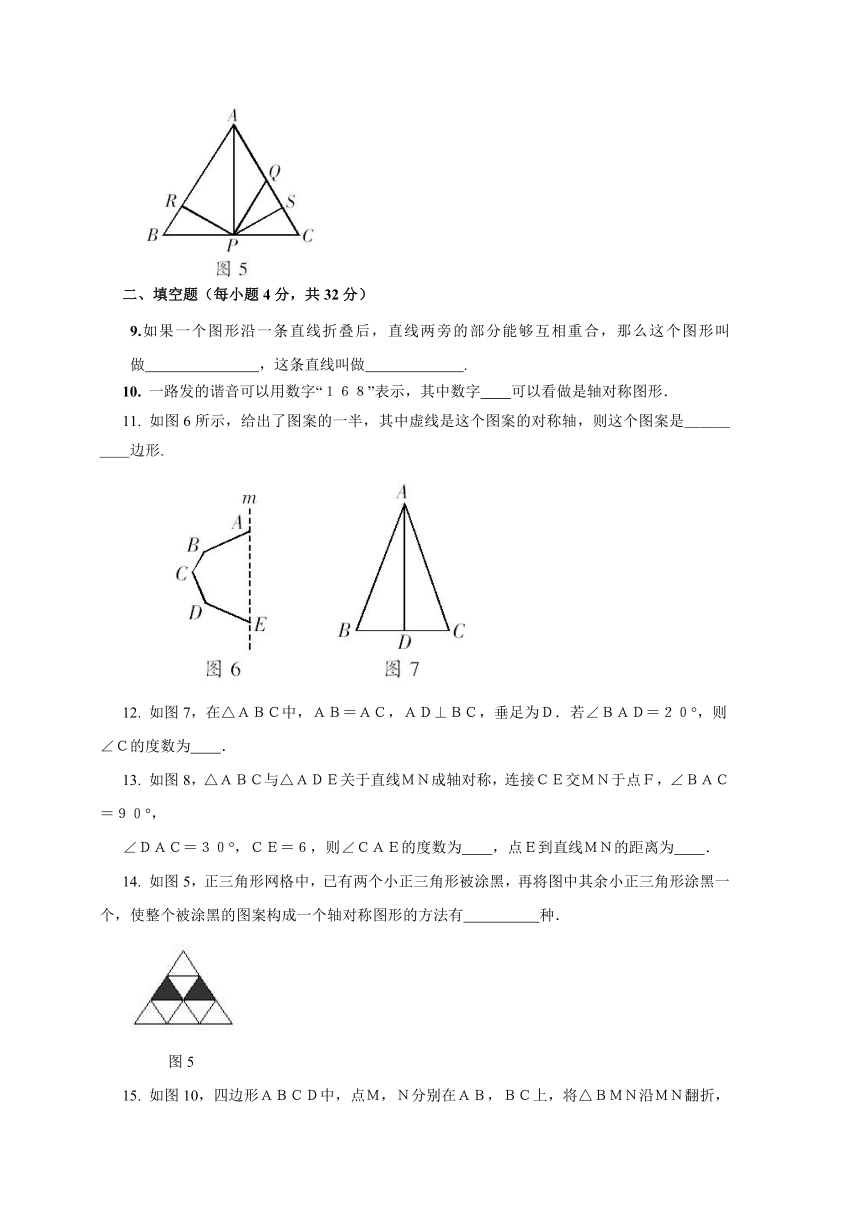
11.
如图6所示,给出了图案的一半,其中虚线是这个图案的对称轴,则这个图案是_____边形.
12.
如图7,在△ABC中,AB=AC,AD⊥BC,垂足为D.若∠BAD=20°,则∠C的度数为
.
13.
如图8,△ABC与△ADE关于直线MN成轴对称,连接CE交MN于点F,∠BAC=90°,
∠DAC=30°,CE=6,则∠CAE的度数为
,点E到直线MN的距离为
.
14.
如图5,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有
种.
图5
15.
如图10,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠B=
°.
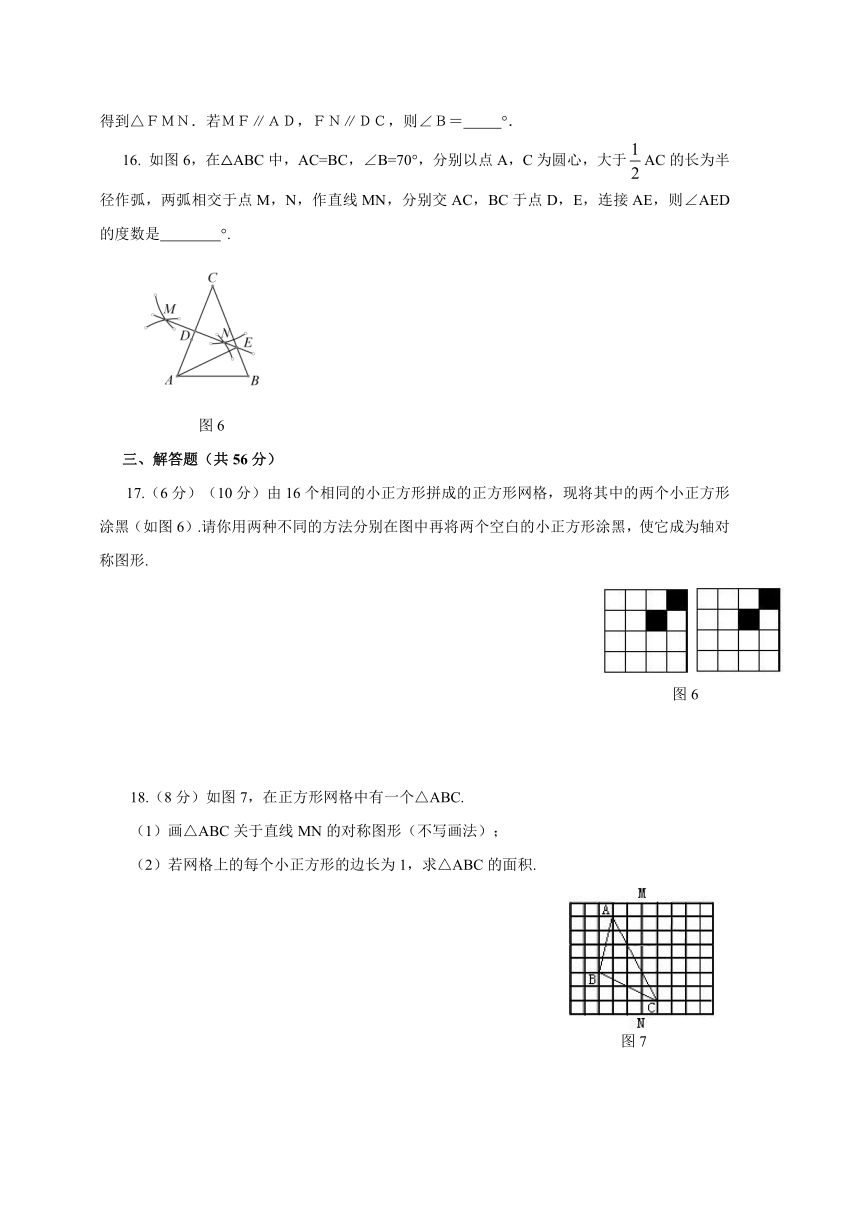
16.
如图6,在△ABC中,AC=BC,∠B=70°,分别以点A,C为圆心,大于AC的长为半径作弧,两弧相交于点M,N,作直线MN,分别交AC,BC于点D,E,连接AE,则∠AED的度数是
°.
图6
三、解答题(共56分)
17.(6分)(10分)由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图6).请你用两种不同的方法分别在图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
18.(8分)如图7,在正方形网格中有一个△ABC.
(1)画△ABC关于直线MN的对称图形(不写画法);
(2)若网格上的每个小正方形的边长为1,求△ABC的面积.
19.(10分)如图9,在△ABC中,利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作∠CBD的平分线BM;
②作边BC上的中线AE,与BC相交于点E.
图9
20.(10分)(1)观察图9的①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;
(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与①~④的图案不能重合)
21.(10分)如图11,在Rt△ABC中,∠ACB=90 ,∠B=30 ,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,DA与DE相等吗?为什么?
图11
22.(12分)如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
参考答案
一、1.
B
2.
C
3.
A
4.
C
5.
D
6.
C
7.
D
8.
A
二、9.
轴对称图形
对称轴
10.
8
11.
八
12.
70°
13.
60°
3
14.
3
15.
80
16.
50
三、17.
解:答案不唯一,给出两种如图1所示.
18.
解:(1)如图2所示,△A′B′C′即为所求作三角形.
(2)S△ABC=9.
19.
解:如图3所示,BM为∠CBD的平分线,AE为边BC上的中线.
20.
解:(1)两个共同特征是:①都是轴对称图形;②它们的面积都等于4个小正方形的面积之和.
(2)答案不唯一,如图4所示.
21.
解:(1)因为∠ACB=90°,所以∠CAB+∠B=90°.
又因为∠B=30°,所以∠CAB=60°.
因为AD平分∠CAB,所以∠CAD=30°.
(2)相等.理由如下:
因为∠ACB=90°,所以DC⊥AE.
又因为CE=AC,所以DC垂直平分AE,所以DA=DE.
22.
解:(1)因为点E,F分别是AB,AC的中点,所以AE=AB,AF=AC.又因为AB=AC,所以AE=AF,所以△AEF是等腰三角形.
(2)DE=DF.理由如下:
方法一:因为AD是等腰三角形ABC底边上的高,所以AD也是∠BAC的平分线.
因为△AEF是等腰三角形,所以AG是底边EF上的高和中线,所以AD所在的直线是线段EF的垂直平分线,所以DE=DF.
方法二:因为AD是等腰三角形ABC底边上的高,所以BD=CD.因为点E,F分别是边AB,AC的中点,所以BE=CF.又因为∠B=∠C,所以△BDE≌△CDF(SAS),所以DE=DF.
A
B
C
D
图6
图7
图9
图
11
单元检测题
时间:
分钟
满分:120分
班级:
姓名:
得分:
一、选择题(每小题4分,共32分)
1.图1所示的图形中,轴对称图形有(
)
A.4个
B.3个
C.2个
D.1个
图1
2.下列说法中错误的是(
)
A.两个关于某直线对称的图形一定能够完全重合
B.成轴对称的两个图形,其对应点的连线的垂直平分线是它们的对称轴
C.对称图形的对称点一定在对称轴的两侧
D.平面上两个能够完全重合的图形不一定关于某直线对称
3.下列分子结构模型平面图中,只有一条对称轴的是(
)
4.下列说法中,正确的是(
)
A.等腰三角形底边上的中线就是底边的垂直平分线
B.等腰三角形的对称轴是底边上的高
C.一条线段可看做是以它的垂直平分线为对称轴的轴对称图形
D.等腰三角形的对称轴就是顶角平分线
5.如图2,△ABC中,AB=AC,∠B=70°,则∠C的度数是( )
A.
40°
B.
50°
C.
55°
D.
70°
6.
如图3,如果直线l是多边形ABCDE的对称轴,其中∠A=120°,∠C=110°,那么∠E的度数为(
)
A.
60°
B.
70°
C.
110°
D.
120°
7.如图4所示,将一个正方形纸片依次按图,图的方式对折,然后沿图中的虚线裁剪,最后将图的纸再展开铺平,所看到的图案是(
).
a
b
c
d
图4
8.如图5,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,有下列说法:①点P在∠A的平分线上;
②AS=AR;
③QP∥AR;④△BRP≌△QSP.其中正确的是(
)
A.全部正确
B.仅①②正确
C.仅②③正确
D.仅①③正确
二、填空题(每小题4分,共32分)
9.如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做
,这条直线叫做
.
10.
一路发的谐音可以用数字“168”表示,其中数字
可以看做是轴对称图形.
11.
如图6所示,给出了图案的一半,其中虚线是这个图案的对称轴,则这个图案是_____边形.
12.
如图7,在△ABC中,AB=AC,AD⊥BC,垂足为D.若∠BAD=20°,则∠C的度数为
.
13.
如图8,△ABC与△ADE关于直线MN成轴对称,连接CE交MN于点F,∠BAC=90°,
∠DAC=30°,CE=6,则∠CAE的度数为
,点E到直线MN的距离为
.
14.
如图5,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有
种.
图5
15.
如图10,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠B=
°.
16.
如图6,在△ABC中,AC=BC,∠B=70°,分别以点A,C为圆心,大于AC的长为半径作弧,两弧相交于点M,N,作直线MN,分别交AC,BC于点D,E,连接AE,则∠AED的度数是
°.
图6
三、解答题(共56分)
17.(6分)(10分)由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图6).请你用两种不同的方法分别在图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
18.(8分)如图7,在正方形网格中有一个△ABC.
(1)画△ABC关于直线MN的对称图形(不写画法);
(2)若网格上的每个小正方形的边长为1,求△ABC的面积.
19.(10分)如图9,在△ABC中,利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作∠CBD的平分线BM;
②作边BC上的中线AE,与BC相交于点E.
图9
20.(10分)(1)观察图9的①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征;
(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与①~④的图案不能重合)
21.(10分)如图11,在Rt△ABC中,∠ACB=90 ,∠B=30 ,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,DA与DE相等吗?为什么?
图11
22.(12分)如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
参考答案
一、1.
B
2.
C
3.
A
4.
C
5.
D
6.
C
7.
D
8.
A
二、9.
轴对称图形
对称轴
10.
8
11.
八
12.
70°
13.
60°
3
14.
3
15.
80
16.
50
三、17.
解:答案不唯一,给出两种如图1所示.
18.
解:(1)如图2所示,△A′B′C′即为所求作三角形.
(2)S△ABC=9.
19.
解:如图3所示,BM为∠CBD的平分线,AE为边BC上的中线.
20.
解:(1)两个共同特征是:①都是轴对称图形;②它们的面积都等于4个小正方形的面积之和.
(2)答案不唯一,如图4所示.
21.
解:(1)因为∠ACB=90°,所以∠CAB+∠B=90°.
又因为∠B=30°,所以∠CAB=60°.
因为AD平分∠CAB,所以∠CAD=30°.
(2)相等.理由如下:
因为∠ACB=90°,所以DC⊥AE.
又因为CE=AC,所以DC垂直平分AE,所以DA=DE.
22.
解:(1)因为点E,F分别是AB,AC的中点,所以AE=AB,AF=AC.又因为AB=AC,所以AE=AF,所以△AEF是等腰三角形.
(2)DE=DF.理由如下:
方法一:因为AD是等腰三角形ABC底边上的高,所以AD也是∠BAC的平分线.
因为△AEF是等腰三角形,所以AG是底边EF上的高和中线,所以AD所在的直线是线段EF的垂直平分线,所以DE=DF.
方法二:因为AD是等腰三角形ABC底边上的高,所以BD=CD.因为点E,F分别是边AB,AC的中点,所以BE=CF.又因为∠B=∠C,所以△BDE≌△CDF(SAS),所以DE=DF.
A
B
C
D
图6
图7
图9
图
11
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
