2016—2017北师大版数学七年级下册单元检测题_第三章变量之间的关系
文档属性
| 名称 | 2016—2017北师大版数学七年级下册单元检测题_第三章变量之间的关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 200.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-11 00:00:00 | ||
图片预览

文档简介
第三章
变量之间的关系
单元检测题
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.在关于圆的面积的表达式S=πr2中,变量有(
)
A.4个
B.3个
C.2个
D.1个
2.“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.赵叔叔家距离单位4千米,某天赵叔叔骑自行车从家出发去单位上班,行进速度为5千米/时.若用s(千米)表示赵叔叔距离单位的距离,行驶时间用t(小时)表示,在这个过程中,下列说法正确的是(
)
A.s是自变量,t是因变量
B.s是自变量,v是因变量
C.t是自变量,s是因变量
D.5是自变量,s是因变量
3.2015年7月10日,某河流受暴雨的影响,当日该河流的水位记录如下表:
时间/时
0
4
8
12
16
20
24
水位/米
1.5
2
3.5
5
6
7
9
则下列描述不正确的是(
)
上表反应的是时间与水位之间的关系
随着时间的逐渐增大,水位逐渐增大
20时到24时水位上升最快
12时到20时水位上升最慢
4.华氏温度F(华氏度)与摄氏温度C(摄氏度)之间的关系为F=C+32,若某地某时温度为20摄氏度,则该温度相当于华氏温度为(
)
A.68华氏度
B.-华氏度
C.77华氏度
D.华氏度
5.新农村社区改造中,有一部分楼盘要对外销售.
某楼共30层,从第八层开始,售价x(元/平方米)与楼层n(8≤n<30)之间的关系如下表:
楼层n
8
9
10
11
12
…
售价x(元/平方米)
2000
2050
2100
2150
2200
…
则售价x(元/平方米)与楼层n之间的关系式为
(
)
x=2000+50n
B.x=2000+50(n-8)
C.n=2000+50(x-8)
D.n=2000+50x
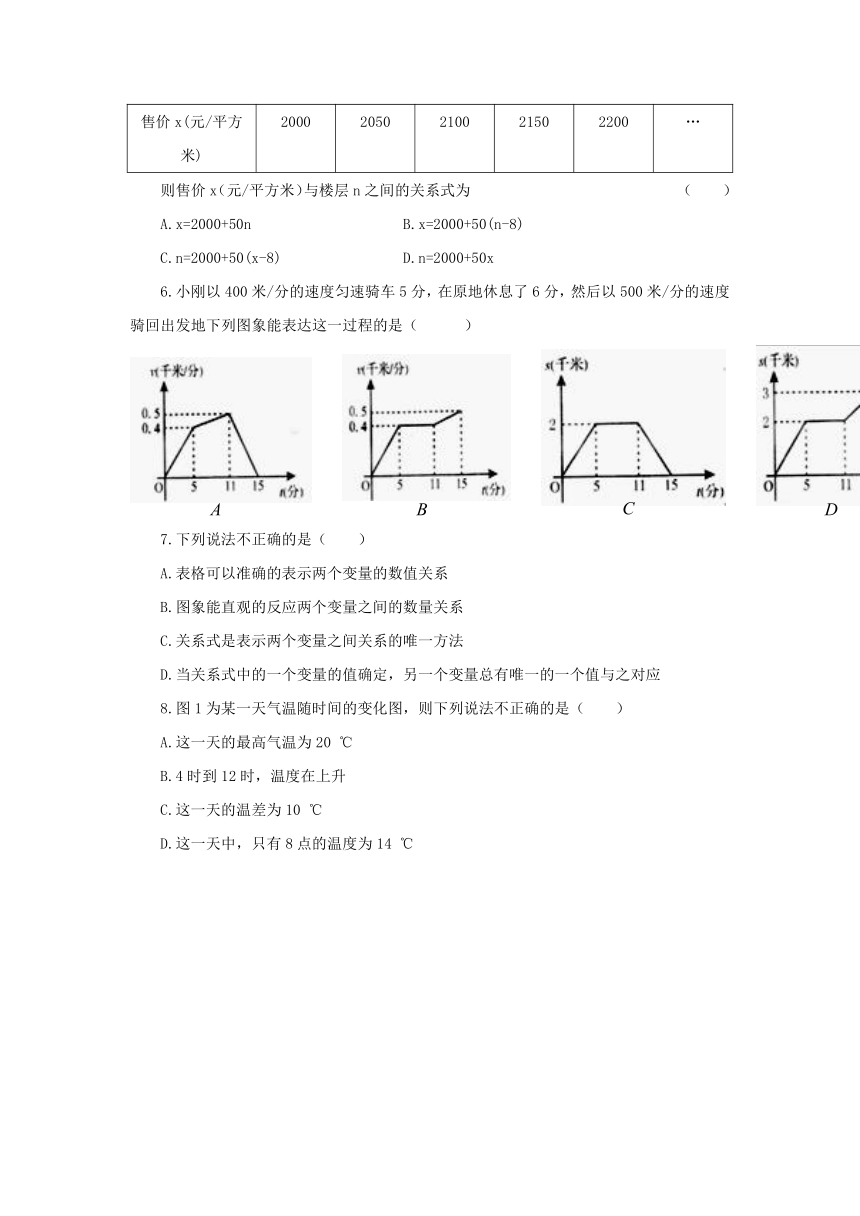
6.小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地下列图象能表达这一过程的是(
)
7.下列说法不正确的是(
)
表格可以准确的表示两个变量的数值关系
图象能直观的反应两个变量之间的数量关系
关系式是表示两个变量之间关系的唯一方法
当关系式中的一个变量的值确定,另一个变量总有唯一的一个值与之对应
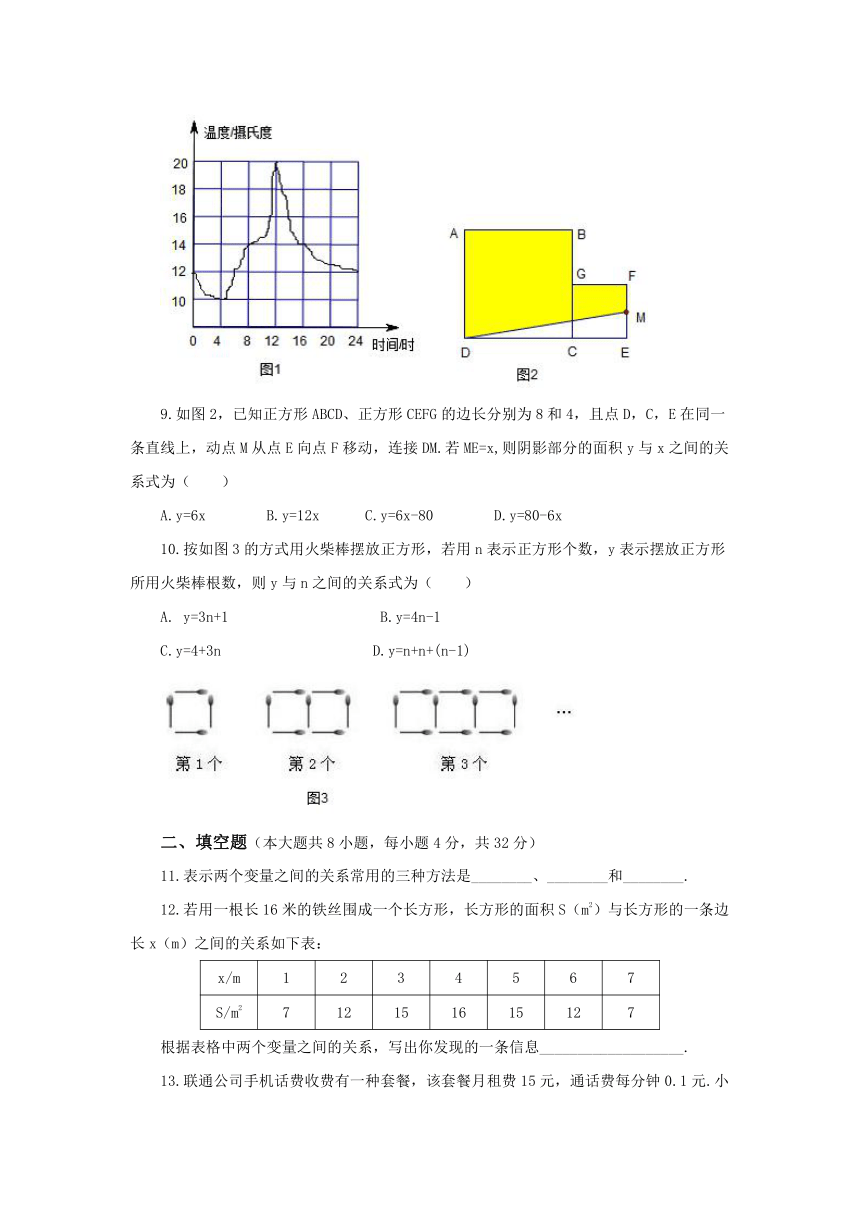
8.图1为某一天气温随时间的变化图,则下列说法不正确的是(
)
A.这一天的最高气温为20
℃
B.4时到12时,温度在上升
C.这一天的温差为10
℃
D.这一天中,只有8点的温度为14
℃
9.如图2,已知正方形ABCD、正方形CEFG的边长分别为8和4,且点D,C,E在同一条直线上,动点M从点E向点F移动,连接DM.若ME=x,则阴影部分的面积y与x之间的关系式为(
)
A.y=6x
B.y=12x
C.y=6x-80
D.y=80-6x
10.按如图3的方式用火柴棒摆放正方形,若用n表示正方形个数,y表示摆放正方形所用火柴棒根数,则y与n之间的关系式为(
)
A.
y=3n+1
B.y=4n-1
C.y=4+3n
D.y=n+n+(n-1)
二、填空题(本大题共8小题,每小题4分,共32分)
11.表示两个变量之间的关系常用的三种方法是________、________和________.
12.若用一根长16米的铁丝围成一个长方形,长方形的面积S(m2)与长方形的一条边长x(m)之间的关系如下表:
x/m
1
2
3
4
5
6
7
S/m2
7
12
15
16
15
12
7
根据表格中两个变量之间的关系,写出你发现的一条信息___________________.
13.联通公司手机话费收费有一种套餐,该套餐月租费15元,通话费每分钟0.1元.小丽用该套餐月话费为y(元),月通话时间为x分,在这个情境中,自变量为_______,因变量为_________.
14.由于地球引力和月球引力的不同,因此,同一物体在地球上的重量和在月球上的重量是不相等的.同一物体在月球上的重量y(千克)与同一物体在地球上的重量x(千克)之间的关系式为y=x,则在地球上重量为120千克的物体,在月球上重量减少了_______千克.
15.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶.汽车行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时)
0
1
2
3
y(升)
100
92
84
76
由表格中的数量关系可知,油箱的余油量y(升)与行驶时间t(小时)之间的关系式为____________,当汽车行驶_______小时,油箱的余油量为0.
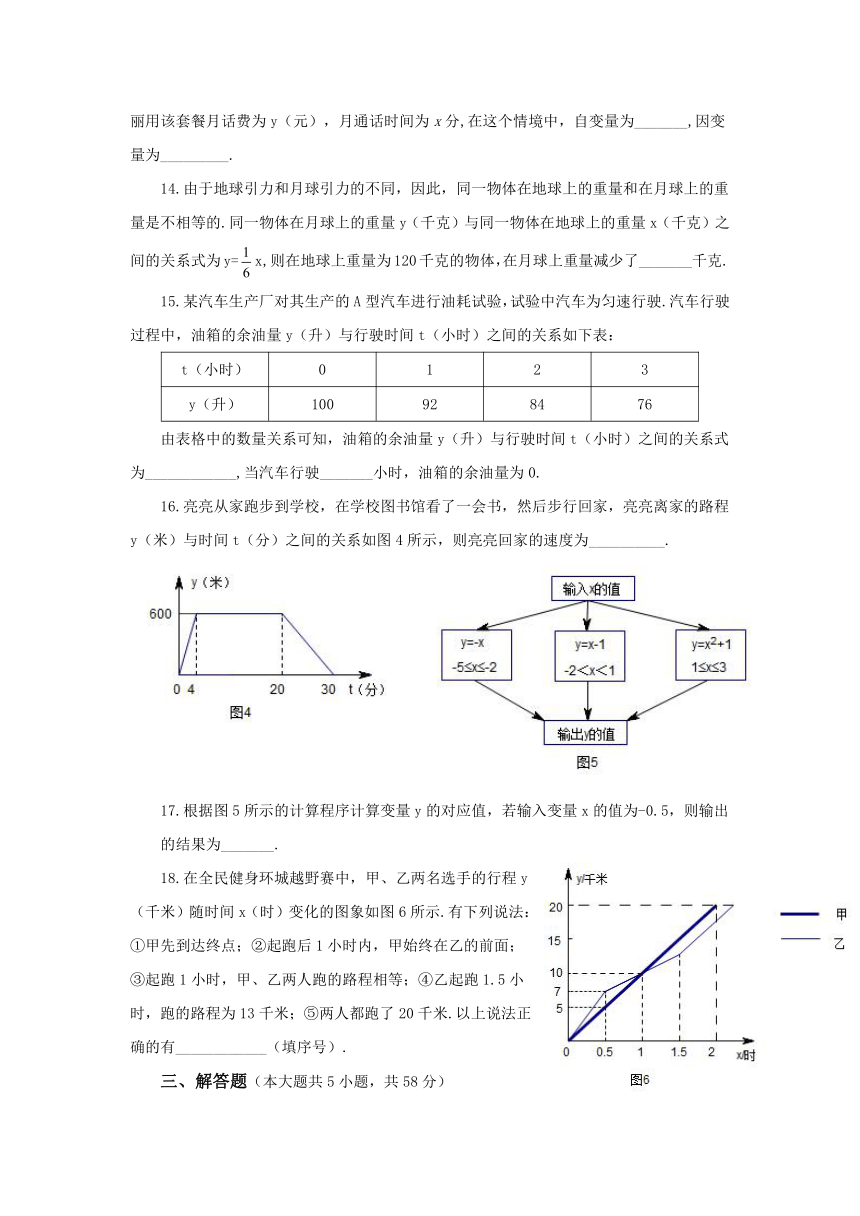
16.亮亮从家跑步到学校,在学校图书馆看了一会书,然后步行回家,亮亮离家的路程y(米)与时间t(分)之间的关系如图4所示,则亮亮回家的速度为__________.
17.根据图5所示的计算程序计算变量y的对应值,若输入变量x的值为-0.5,则输出的结果为_______.
18.在全民健身环城越野赛中,甲、乙两名选手的行程y(千米)随时间x(时)变化的图象如图6所示.有下列说法:①甲先到达终点;②起跑后1小时内,甲始终在乙的前面;③起跑1小时,甲、乙两人跑的路程相等;④乙起跑1.5小时,跑的路程为13千米;⑤两人都跑了20千米.以上说法正确的有____________(填序号).
三、解答题(本大题共5小题,共58分)
19.(9分)物体从高处自由落下,物体下落的高度h(米)与下落的时间t(秒)之间的关系如下表:
h(米)
5
20
45
80
180
…
t(秒)
1
2
3
4
5
…
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
当物体从80米的高处落下时,大约需要多少秒?
随着高度h(米)的变化,下落的时间t(秒)是如何变化的?
(10分)在数轴上,若点A,B表示的数分别为3和x,则A,B之间的距离y与x之间的关系式为y=.
当x的值为-5时,求y的值;
根据关系式,完成下表:
x
-1
0
1
2
3
4
5
6
y
(12分)点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分
0
2
4
6
8
10
h/厘米
30
29
28
27
26
25
蜡烛未点燃前的长度是多少厘米?
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式;
求这根蜡烛能燃烧多长时间.
22.(12分)某水库初始的水位高度为5米,水位在10小时内持续匀速上涨,测量可知,经过4小时,水位上涨了1米.
写出水库的水位高度y(米)与时间x(小时)(0≤x≤10)之间的关系式;
经过______小时,水库的水位上涨到6.5米;
当时间由1小时变化到10小时时,水库的水位高度由______米变化到______米.
23.(15分)星期天,小宇的爸爸9点钟从家里到附近的一个银行办理业务,他走了一段路后,突然发现忘记带身份证,于是他跑步回家,拿了身份证,跑到银行办理业务,办完业务他步行回到家.他离家的路程s(米)与时间t(分)之间的关系如图7所示.
(1)小宇的爸爸几点钟到达银行?他办理业务共用多长时间?
几点钟,小宇的爸爸发现忘记带身份证,此时,他离家多远?
小宇的爸爸在去银行办理业务的过程中走过的路程为多少米?
求小宇爸爸从银行回到家的速度.
附加题(15分,不计入总分)
24.如图
8所示,梯形的上底AD=4,下底BC=6,CD=8,∠C=∠D=90°,点M从点C出发向点D移动,连接AM,BM,假设阴影部分的面积是y,CM的长度为x.
写出变量y与x之间的关系式;
当x=2时,阴影部分的面积是多少?
在点M的移动过程中,是否存在阴影部分的面积等于梯形面积的,若存在,求出x的值;若不存在,简单说明理由.
参考答案
一、1.C
2.C
3.D
4.A
5.B
6.C
7.C
8.D
9.D
提示:阴影部分的面积是两个正方形的面积和减去三角形DEM面积.
10.A
二、11.表格法
关系式法
图象法
12.答案不唯一,合理即可,略
13.
通话时间
月话费
14.100
15.y=100-8t
12.5
16.60米/分
17.-1.5
提示:当x=-0.5时,对应关系式是y=x-1,代入计算得y=-0.5-1=-1.5.
18.①③④⑤
三、19.解:(1)反映了物体下落的高度h(米)与下落的时间t(秒)之间的关系,其中物体下落的高度h(米)是自变量,下落的时间t(秒)是因变量;
(2)4秒;
(3)随着高度h(米)的逐渐增大,下落的时间t(秒)随着增大.
20.
解:(1)当x的值为-5时,y==8.
(2)
x
-1
0
1
2
3
4
5
6
y
4
3
2
1
0
1
2
3
21.
解:(1)蜡烛未点燃前的长度是30厘米;
(2)h=30-0.5t;
(3)当h=0时,得0=30-0.5t.
解方程,得t=60.
所以这根蜡烛能燃烧60分.
22.(1)小宇的爸爸9:16到达银行,他办理业务共用4分.
9:05小宇的爸爸发现忘记带身份证,此时,他离家300米.
(3)300×2+800×2=2200(米).
所以小宇的爸爸在去银行办理业务的过程中走过的路程2200米.
(4)800÷(30-20)=80(米/分).
所以小宇爸爸从银行回到家的速度为80米/分.
23.(1)y=0.25x+5(0≤x≤10);
(2)6
(3)5.25
7.5
附加题
24.(1)y=-x+24;
(2)当x=2时,y=-2+24=22;
(3)不存在,理由:假设存在,则-x+24=××(4+6)×8.解方程,得x=14>8.所以不存在.
变量之间的关系
单元检测题
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.在关于圆的面积的表达式S=πr2中,变量有(
)
A.4个
B.3个
C.2个
D.1个
2.“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.赵叔叔家距离单位4千米,某天赵叔叔骑自行车从家出发去单位上班,行进速度为5千米/时.若用s(千米)表示赵叔叔距离单位的距离,行驶时间用t(小时)表示,在这个过程中,下列说法正确的是(
)
A.s是自变量,t是因变量
B.s是自变量,v是因变量
C.t是自变量,s是因变量
D.5是自变量,s是因变量
3.2015年7月10日,某河流受暴雨的影响,当日该河流的水位记录如下表:
时间/时
0
4
8
12
16
20
24
水位/米
1.5
2
3.5
5
6
7
9
则下列描述不正确的是(
)
上表反应的是时间与水位之间的关系
随着时间的逐渐增大,水位逐渐增大
20时到24时水位上升最快
12时到20时水位上升最慢
4.华氏温度F(华氏度)与摄氏温度C(摄氏度)之间的关系为F=C+32,若某地某时温度为20摄氏度,则该温度相当于华氏温度为(
)
A.68华氏度
B.-华氏度
C.77华氏度
D.华氏度
5.新农村社区改造中,有一部分楼盘要对外销售.
某楼共30层,从第八层开始,售价x(元/平方米)与楼层n(8≤n<30)之间的关系如下表:
楼层n
8
9
10
11
12
…
售价x(元/平方米)
2000
2050
2100
2150
2200
…
则售价x(元/平方米)与楼层n之间的关系式为
(
)
x=2000+50n
B.x=2000+50(n-8)
C.n=2000+50(x-8)
D.n=2000+50x
6.小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地下列图象能表达这一过程的是(
)
7.下列说法不正确的是(
)
表格可以准确的表示两个变量的数值关系
图象能直观的反应两个变量之间的数量关系
关系式是表示两个变量之间关系的唯一方法
当关系式中的一个变量的值确定,另一个变量总有唯一的一个值与之对应
8.图1为某一天气温随时间的变化图,则下列说法不正确的是(
)
A.这一天的最高气温为20
℃
B.4时到12时,温度在上升
C.这一天的温差为10
℃
D.这一天中,只有8点的温度为14
℃
9.如图2,已知正方形ABCD、正方形CEFG的边长分别为8和4,且点D,C,E在同一条直线上,动点M从点E向点F移动,连接DM.若ME=x,则阴影部分的面积y与x之间的关系式为(
)
A.y=6x
B.y=12x
C.y=6x-80
D.y=80-6x
10.按如图3的方式用火柴棒摆放正方形,若用n表示正方形个数,y表示摆放正方形所用火柴棒根数,则y与n之间的关系式为(
)
A.
y=3n+1
B.y=4n-1
C.y=4+3n
D.y=n+n+(n-1)
二、填空题(本大题共8小题,每小题4分,共32分)
11.表示两个变量之间的关系常用的三种方法是________、________和________.
12.若用一根长16米的铁丝围成一个长方形,长方形的面积S(m2)与长方形的一条边长x(m)之间的关系如下表:
x/m
1
2
3
4
5
6
7
S/m2
7
12
15
16
15
12
7
根据表格中两个变量之间的关系,写出你发现的一条信息___________________.
13.联通公司手机话费收费有一种套餐,该套餐月租费15元,通话费每分钟0.1元.小丽用该套餐月话费为y(元),月通话时间为x分,在这个情境中,自变量为_______,因变量为_________.
14.由于地球引力和月球引力的不同,因此,同一物体在地球上的重量和在月球上的重量是不相等的.同一物体在月球上的重量y(千克)与同一物体在地球上的重量x(千克)之间的关系式为y=x,则在地球上重量为120千克的物体,在月球上重量减少了_______千克.
15.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶.汽车行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时)
0
1
2
3
y(升)
100
92
84
76
由表格中的数量关系可知,油箱的余油量y(升)与行驶时间t(小时)之间的关系式为____________,当汽车行驶_______小时,油箱的余油量为0.
16.亮亮从家跑步到学校,在学校图书馆看了一会书,然后步行回家,亮亮离家的路程y(米)与时间t(分)之间的关系如图4所示,则亮亮回家的速度为__________.
17.根据图5所示的计算程序计算变量y的对应值,若输入变量x的值为-0.5,则输出的结果为_______.
18.在全民健身环城越野赛中,甲、乙两名选手的行程y(千米)随时间x(时)变化的图象如图6所示.有下列说法:①甲先到达终点;②起跑后1小时内,甲始终在乙的前面;③起跑1小时,甲、乙两人跑的路程相等;④乙起跑1.5小时,跑的路程为13千米;⑤两人都跑了20千米.以上说法正确的有____________(填序号).
三、解答题(本大题共5小题,共58分)
19.(9分)物体从高处自由落下,物体下落的高度h(米)与下落的时间t(秒)之间的关系如下表:
h(米)
5
20
45
80
180
…
t(秒)
1
2
3
4
5
…
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
当物体从80米的高处落下时,大约需要多少秒?
随着高度h(米)的变化,下落的时间t(秒)是如何变化的?
(10分)在数轴上,若点A,B表示的数分别为3和x,则A,B之间的距离y与x之间的关系式为y=.
当x的值为-5时,求y的值;
根据关系式,完成下表:
x
-1
0
1
2
3
4
5
6
y
(12分)点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分
0
2
4
6
8
10
h/厘米
30
29
28
27
26
25
蜡烛未点燃前的长度是多少厘米?
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式;
求这根蜡烛能燃烧多长时间.
22.(12分)某水库初始的水位高度为5米,水位在10小时内持续匀速上涨,测量可知,经过4小时,水位上涨了1米.
写出水库的水位高度y(米)与时间x(小时)(0≤x≤10)之间的关系式;
经过______小时,水库的水位上涨到6.5米;
当时间由1小时变化到10小时时,水库的水位高度由______米变化到______米.
23.(15分)星期天,小宇的爸爸9点钟从家里到附近的一个银行办理业务,他走了一段路后,突然发现忘记带身份证,于是他跑步回家,拿了身份证,跑到银行办理业务,办完业务他步行回到家.他离家的路程s(米)与时间t(分)之间的关系如图7所示.
(1)小宇的爸爸几点钟到达银行?他办理业务共用多长时间?
几点钟,小宇的爸爸发现忘记带身份证,此时,他离家多远?
小宇的爸爸在去银行办理业务的过程中走过的路程为多少米?
求小宇爸爸从银行回到家的速度.
附加题(15分,不计入总分)
24.如图
8所示,梯形的上底AD=4,下底BC=6,CD=8,∠C=∠D=90°,点M从点C出发向点D移动,连接AM,BM,假设阴影部分的面积是y,CM的长度为x.
写出变量y与x之间的关系式;
当x=2时,阴影部分的面积是多少?
在点M的移动过程中,是否存在阴影部分的面积等于梯形面积的,若存在,求出x的值;若不存在,简单说明理由.
参考答案
一、1.C
2.C
3.D
4.A
5.B
6.C
7.C
8.D
9.D
提示:阴影部分的面积是两个正方形的面积和减去三角形DEM面积.
10.A
二、11.表格法
关系式法
图象法
12.答案不唯一,合理即可,略
13.
通话时间
月话费
14.100
15.y=100-8t
12.5
16.60米/分
17.-1.5
提示:当x=-0.5时,对应关系式是y=x-1,代入计算得y=-0.5-1=-1.5.
18.①③④⑤
三、19.解:(1)反映了物体下落的高度h(米)与下落的时间t(秒)之间的关系,其中物体下落的高度h(米)是自变量,下落的时间t(秒)是因变量;
(2)4秒;
(3)随着高度h(米)的逐渐增大,下落的时间t(秒)随着增大.
20.
解:(1)当x的值为-5时,y==8.
(2)
x
-1
0
1
2
3
4
5
6
y
4
3
2
1
0
1
2
3
21.
解:(1)蜡烛未点燃前的长度是30厘米;
(2)h=30-0.5t;
(3)当h=0时,得0=30-0.5t.
解方程,得t=60.
所以这根蜡烛能燃烧60分.
22.(1)小宇的爸爸9:16到达银行,他办理业务共用4分.
9:05小宇的爸爸发现忘记带身份证,此时,他离家300米.
(3)300×2+800×2=2200(米).
所以小宇的爸爸在去银行办理业务的过程中走过的路程2200米.
(4)800÷(30-20)=80(米/分).
所以小宇爸爸从银行回到家的速度为80米/分.
23.(1)y=0.25x+5(0≤x≤10);
(2)6
(3)5.25
7.5
附加题
24.(1)y=-x+24;
(2)当x=2时,y=-2+24=22;
(3)不存在,理由:假设存在,则-x+24=××(4+6)×8.解方程,得x=14>8.所以不存在.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
