湘教版数学七年级上册第4章 图形的认识 测试题
文档属性
| 名称 | 湘教版数学七年级上册第4章 图形的认识 测试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 219.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-12 11:26:41 | ||
图片预览


文档简介
第4章
图形的认识测试题
(本试卷满分120分,含附加题20分)
一、选择题(每小题3分,共30分)
1.
把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.垂线段最短
C.两点之间线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
2.
从左面观察图1所示的立体图形,能得到的平面图形是(
)
A
B
C
D
图1
3.
下列四个图中角的表示方法正确的是(
)
4.
下列图形中,不是立体图形的是(
)
A.
圆锥
B.
六棱柱
C.
圆
D.
圆柱
5.下列说法:①线段有两个端点,直线有一个端点;②角的大小与角的两边的长短无关;③线段上有
无数个点;④同角或等角的补角相等;⑤两个锐角的和一定大于直角.
其中错误的说法有(
)
A.1个
B.2个
C.3个
D.4个
6.下列单位换算中,不正确的是
(
)
A.
1.5°=90′
B.
120″=2′
C.
2°5′=3900″
D.
10.3°=36720″
7.
已知M是线段AB的中点,下列结论错误的是(
)
A.AM+BM=AB
B.AB=2AM
C.BM=AB
D.AM=BM
8.
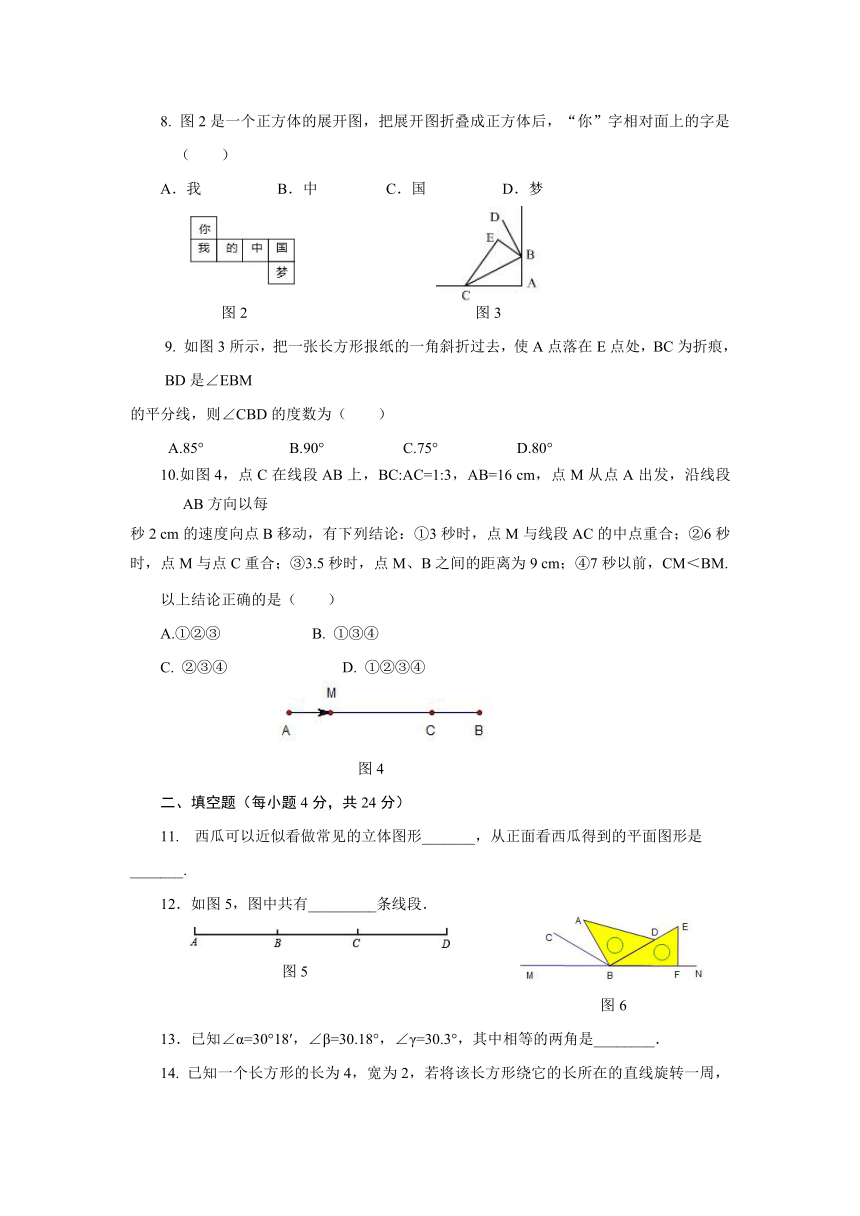
图2是一个正方体的展开图,把展开图折叠成正方体后,“你”字相对面上的字是( )
A.我
B.中
C.国
D.梦
图2
图3
9.
如图3所示,把一张长方形报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM
的平分线,则∠CBD的度数为(
)
A.85°
B.90°
C.75°
D.80°
10.如图4,点C在线段AB上,BC:AC=1:3,AB=16
cm,点M从点A出发,沿线段AB方向以每
秒2
cm的速度向点B移动,有下列结论:①3秒时,点M与线段AC的中点重合;②6秒时,点M与点C重合;③3.5秒时,点M、B之间的距离为9
cm;④7秒以前,CM<BM.
以上结论正确的是(
)
①②③
B.
①③④
C.
②③④
D.
①②③④
图4
二、填空题(每小题4分,共24分)
11.
西瓜可以近似看做常见的立体图形_______,从正面看西瓜得到的平面图形是_______.
12.如图5,图中共有_________条线段.
图5
图6
13.已知∠α=30°18′,∠β=30.18°,∠γ=30.3°,其中相等的两角是________.
14.
已知一个长方形的长为4,宽为2,若将该长方形绕它的长所在的直线旋转一周,得到的几何体是
________,它的体积是________.(π取3)
15.下列几何体:①圆柱;②六棱柱;③圆锥;④长方体.其中侧面展开图是长方形的几何体有:________.(填序号)
16.
将一副三角尺按如图6所示的方式摆放,其中点B,F在直线MN上,BC是∠ABM的平分线,则∠MBC的度数为______.
17.
已知线段AB=8
cm,在直线AB上画线段BC,使它等于3
cm,则线段
AC=_______cm.
18.
如图7,射线OA的方向是________,
射线OB的方向是_________,
射线OC的方向是________.
图7
三、解答题(共46分)
19.
(6分)将图8所示的几何体与它的名称用线连接起来.
图8
20.
(8分)计算:已知∠A=8.6°,∠B=5°24′.
(1)∠A与∠B的和等于多少分?
(2)∠A与∠B的差等于多少度?
21.(8分)图9是由7个小正方体组成的一个几何体,画出分别从正面、左面、上面看该几何体得到的平面图行.
图9
22.
(8分)如图10,已知D是AB的中点,
E是BC的中点,BE=AC=2
cm,
求线段DE的长.
图10
23.
(8分)如图11,AB和CD都是直线,已知∠AOE=90°,∠3=∠FOD,∠1=27°20′,求∠2,∠3
的度数.
图11
24.
(8分)如图12,在正方体ABCD-A1B1C1D1中.
(1)分别写出以点B为端点的线段;
(2)一只蚂蚁要从A点沿表面爬行到顶点B1,怎样爬行路线最短?为什么?
(3)若由点A沿表面爬行到点C1呢?
图12
附加题(共20分)
24.
(10分)如图13,已知O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
图13
26.
(10分)(1)探索知识:在图14-①中,有3条射线,共有3个角;在图18-②中有_____条射线,共有_____个角;在图14-③中有_____条射线,共有_____个角;
(2)猜想验证:仿照图14的画法,若图中有6条射线,则共有______个角;
(3)归纳总结:仿照图14的画法,若图中有n(n≥2)条射线,则共有______个角.
参考答案
一、1.C
2.A
3.D
4.C
5.B
6.D
7.A
8.D
9.B
10.D
二、11.球
圆
12.6
13.∠α与∠γ
14.
16.30°
17.
5或11
18.
北偏东15°
北偏西40°
南偏东45°
三、19.
如图1所示.
图1
20.解:(1)∠A+∠B=8.6°+5°24′=516′+324′=840′.
(2)∠A+∠B=8.6°-5°24′=8.6°-5.4°=3.2°.
21.解:如图2所示.
从正面看
从左面看
从上面看
图2
22.
解:因为BE=AC=2
cm,所以AC=10
cm.
又E是BC的中点,所以BC=2BE=4
cm.
所以AB=AC-BC=10-4=6(cm).
因为D是AB的中点,所以DB=AB=3
cm.
所以DE=DB+BE=3+2=5(cm).
23.解:因为∠AOE=90°,
所以∠2=90°-∠1=90°-27°20′=62°40′.
又∠AOD=180°-∠1=152°40′,∠3=∠FOD,所以∠3=∠AOD=76°20′.
24.
解:(1)BA,BC,BB1;
(2)连接AB1,沿AB1路线爬行最短,因为两点之间,线段最短;
(3)将正方体部分展开,连接AC1,沿AC1路线爬行最短.
25.
解:(1)图中有9个小于平角的角.
(2)因为OD平分∠AOC,∠AOC
=50°,所以∠AOD
==25°.
所以∠BOD=180°-25°=155°.
(3)因为
∠BOE
=180°-∠DOE-∠AOD=180°-90°-25°=65°,∠COE
=
90°-25°=65
,所以
∠BOE
=
∠COE,即OE平分∠BOE.
26.
解:(1)4
6
5
10
(2)15
(3)
①
②
③
图14
图形的认识测试题
(本试卷满分120分,含附加题20分)
一、选择题(每小题3分,共30分)
1.
把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.垂线段最短
C.两点之间线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
2.
从左面观察图1所示的立体图形,能得到的平面图形是(
)
A
B
C
D
图1
3.
下列四个图中角的表示方法正确的是(
)
4.
下列图形中,不是立体图形的是(
)
A.
圆锥
B.
六棱柱
C.
圆
D.
圆柱
5.下列说法:①线段有两个端点,直线有一个端点;②角的大小与角的两边的长短无关;③线段上有
无数个点;④同角或等角的补角相等;⑤两个锐角的和一定大于直角.
其中错误的说法有(
)
A.1个
B.2个
C.3个
D.4个
6.下列单位换算中,不正确的是
(
)
A.
1.5°=90′
B.
120″=2′
C.
2°5′=3900″
D.
10.3°=36720″
7.
已知M是线段AB的中点,下列结论错误的是(
)
A.AM+BM=AB
B.AB=2AM
C.BM=AB
D.AM=BM
8.
图2是一个正方体的展开图,把展开图折叠成正方体后,“你”字相对面上的字是( )
A.我
B.中
C.国
D.梦
图2
图3
9.
如图3所示,把一张长方形报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM
的平分线,则∠CBD的度数为(
)
A.85°
B.90°
C.75°
D.80°
10.如图4,点C在线段AB上,BC:AC=1:3,AB=16
cm,点M从点A出发,沿线段AB方向以每
秒2
cm的速度向点B移动,有下列结论:①3秒时,点M与线段AC的中点重合;②6秒时,点M与点C重合;③3.5秒时,点M、B之间的距离为9
cm;④7秒以前,CM<BM.
以上结论正确的是(
)
①②③
B.
①③④
C.
②③④
D.
①②③④
图4
二、填空题(每小题4分,共24分)
11.
西瓜可以近似看做常见的立体图形_______,从正面看西瓜得到的平面图形是_______.
12.如图5,图中共有_________条线段.
图5
图6
13.已知∠α=30°18′,∠β=30.18°,∠γ=30.3°,其中相等的两角是________.
14.
已知一个长方形的长为4,宽为2,若将该长方形绕它的长所在的直线旋转一周,得到的几何体是
________,它的体积是________.(π取3)
15.下列几何体:①圆柱;②六棱柱;③圆锥;④长方体.其中侧面展开图是长方形的几何体有:________.(填序号)
16.
将一副三角尺按如图6所示的方式摆放,其中点B,F在直线MN上,BC是∠ABM的平分线,则∠MBC的度数为______.
17.
已知线段AB=8
cm,在直线AB上画线段BC,使它等于3
cm,则线段
AC=_______cm.
18.
如图7,射线OA的方向是________,
射线OB的方向是_________,
射线OC的方向是________.
图7
三、解答题(共46分)
19.
(6分)将图8所示的几何体与它的名称用线连接起来.
图8
20.
(8分)计算:已知∠A=8.6°,∠B=5°24′.
(1)∠A与∠B的和等于多少分?
(2)∠A与∠B的差等于多少度?
21.(8分)图9是由7个小正方体组成的一个几何体,画出分别从正面、左面、上面看该几何体得到的平面图行.
图9
22.
(8分)如图10,已知D是AB的中点,
E是BC的中点,BE=AC=2
cm,
求线段DE的长.
图10
23.
(8分)如图11,AB和CD都是直线,已知∠AOE=90°,∠3=∠FOD,∠1=27°20′,求∠2,∠3
的度数.
图11
24.
(8分)如图12,在正方体ABCD-A1B1C1D1中.
(1)分别写出以点B为端点的线段;
(2)一只蚂蚁要从A点沿表面爬行到顶点B1,怎样爬行路线最短?为什么?
(3)若由点A沿表面爬行到点C1呢?
图12
附加题(共20分)
24.
(10分)如图13,已知O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
图13
26.
(10分)(1)探索知识:在图14-①中,有3条射线,共有3个角;在图18-②中有_____条射线,共有_____个角;在图14-③中有_____条射线,共有_____个角;
(2)猜想验证:仿照图14的画法,若图中有6条射线,则共有______个角;
(3)归纳总结:仿照图14的画法,若图中有n(n≥2)条射线,则共有______个角.
参考答案
一、1.C
2.A
3.D
4.C
5.B
6.D
7.A
8.D
9.B
10.D
二、11.球
圆
12.6
13.∠α与∠γ
14.
16.30°
17.
5或11
18.
北偏东15°
北偏西40°
南偏东45°
三、19.
如图1所示.
图1
20.解:(1)∠A+∠B=8.6°+5°24′=516′+324′=840′.
(2)∠A+∠B=8.6°-5°24′=8.6°-5.4°=3.2°.
21.解:如图2所示.
从正面看
从左面看
从上面看
图2
22.
解:因为BE=AC=2
cm,所以AC=10
cm.
又E是BC的中点,所以BC=2BE=4
cm.
所以AB=AC-BC=10-4=6(cm).
因为D是AB的中点,所以DB=AB=3
cm.
所以DE=DB+BE=3+2=5(cm).
23.解:因为∠AOE=90°,
所以∠2=90°-∠1=90°-27°20′=62°40′.
又∠AOD=180°-∠1=152°40′,∠3=∠FOD,所以∠3=∠AOD=76°20′.
24.
解:(1)BA,BC,BB1;
(2)连接AB1,沿AB1路线爬行最短,因为两点之间,线段最短;
(3)将正方体部分展开,连接AC1,沿AC1路线爬行最短.
25.
解:(1)图中有9个小于平角的角.
(2)因为OD平分∠AOC,∠AOC
=50°,所以∠AOD
==25°.
所以∠BOD=180°-25°=155°.
(3)因为
∠BOE
=180°-∠DOE-∠AOD=180°-90°-25°=65°,∠COE
=
90°-25°=65
,所以
∠BOE
=
∠COE,即OE平分∠BOE.
26.
解:(1)4
6
5
10
(2)15
(3)
①
②
③
图14
同课章节目录
