苏科版数学八年级上册单元检测 第3章 勾股定理综合测评(含答案)
文档属性
| 名称 | 苏科版数学八年级上册单元检测 第3章 勾股定理综合测评(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-12 13:24:43 | ||
图片预览

文档简介
第3章
勾股定理综合测评
(时间:
满分:120分)
(班级:
姓名:
得分:
)
一、精心选一选(每小题3分,共30分)
1.下列各组线段中,能构成直角三角形的是( )
A.
4,5,6
B.,,
C.
1,,
D.
4,6,8
2.
下列各组数中,是勾股数的是(
)
A.
2,3,4
B.
6,8,9
C.
5,11,13
D.
9,40,41
3.图1所示是某学校的长方形操场,如果一学生要从操场A角走到C角,至少要走( )
A.140
m
B.120
m
C.100
m
D.90
m
图1
图2
图3
4.下列说法正确的是( )
A.若a,b,c是△ABC的三边长,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边长,∠B=90°,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边长,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边长,∠C=90°,则a2+b2=c2
5.已知等腰三角形的腰长为10
cm,底边长为16
cm,则这个等腰三角形的面积为( )
A.96
cm2
B.48
cm2
C.24
cm2
D.32
cm2
6.一个直角三角形的两条边长分别是9和12,则第三边的平方是( )
A.225
B.441
C.63或225
D.63
7.某中学旁边有一块三角形空地,为了保持水土,美化环境,全校师生齐动手,在空地的三条边上栽上了树苗(如图2所示).已知三边上的树苗数分别为56,49,74,空地的三个角均有一棵树,且每条边上的树苗株距(相邻两树苗间的距离)均为1
m,那么这块空地的形状为( )
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
不能确定
8.一艘小船早上8:00从港口出发,以8海里/时的速度向东航行,1小时后,另一艘小船以12海里/时的速度由同一港口出发向南航行,到上午10:00两艘小船相距( )
A.
20海里
B.
15海里
C.
13海里
D.
12海里
9.图3中所有三角形都是直角三角形,所有四边形都是正方形.已知S1
,S2,S3,S4,S分别表示所在正方形的面积,若S1=4,S2=9,S3=8,S4=10,则S的值为( )
A.25
B.31
C.32
D.40
10.图4所示是验证勾股定理采用的一种图形,其中两个全等的直角三角形边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.
B.
图4
C.
D.
二、细心填一填(每小题3分,共24分)
11.在△ABC中,∠C=90°,AB=10,BC=8,则AC的长为________.
12.一根电线杆高8
m,为了安全起见,工人师傅在电线杆顶部到与电线杆底部水平距离6
m处加了一根拉线,发现所用拉线长为10.3
m(不计捆绑部分),则电线杆与地面__________(填“垂直”或“不垂直”).
13.
在Rt△ABC中,已知斜边AB的长为2,则AB2+BC2+CA2=
.
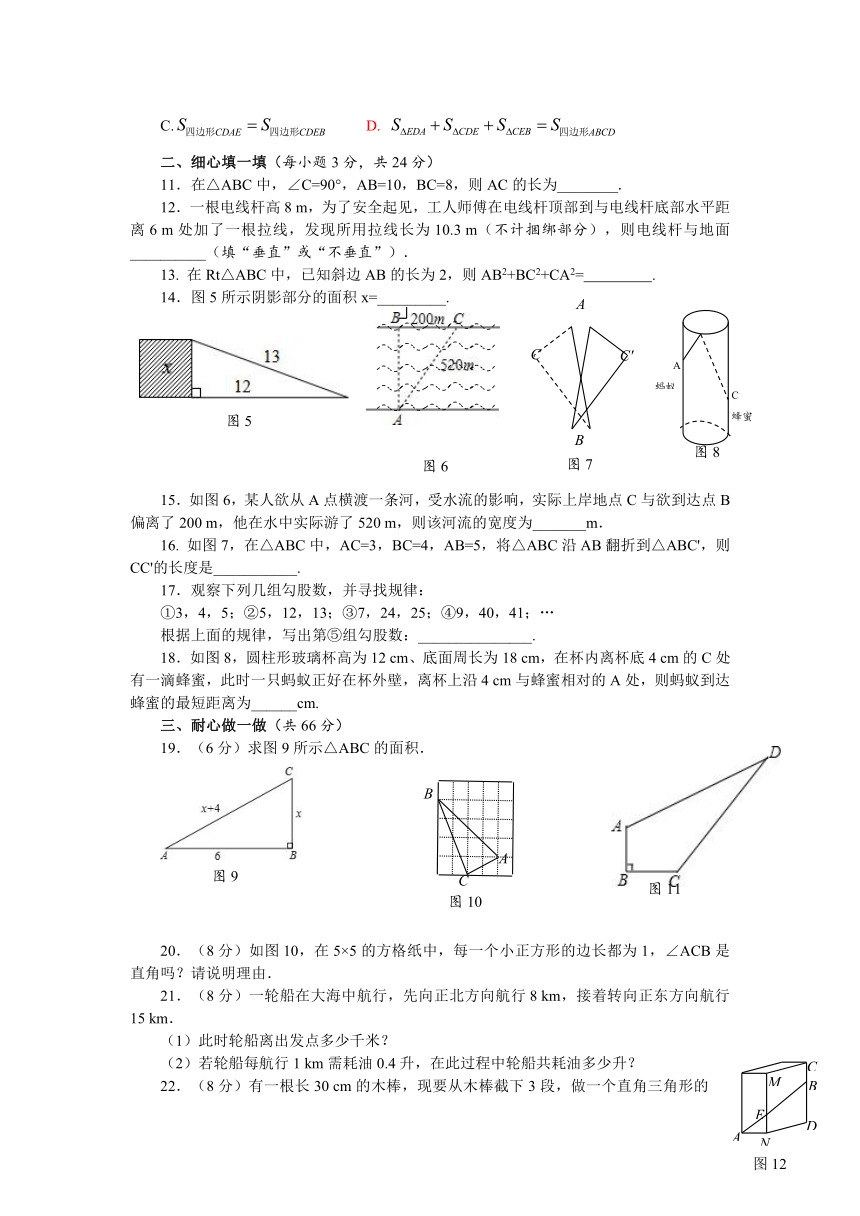
14.图5所示阴影部分的面积x=_________.
15.如图6,某人欲从A点横渡一条河,受水流的影响,实际上岸地点C与欲到达点B偏离了200
m,他在水中实际游了520
m,则该河流的宽度为_______m.
16.
如图7,在△ABC中,AC=3,BC=4,AB=5,将△ABC沿AB翻折到△ABC',则CC'的长度是___________.
17.观察下列几组勾股数,并寻找规律:
①3,4,5;②5,12,13;③7,24,25;④9,40,41;…
根据上面的规律,写出第⑤组勾股数:_______________.
18.如图8,圆柱形玻璃杯高为12
cm、底面周长为18
cm,在杯内离杯底4
cm的C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4
cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离为______cm.
三、耐心做一做(共66分)
19.(6分)求图9所示△ABC的面积.
20.(8分)如图10,在5×5的方格纸中,每一个小正方形的边长都为1,∠ACB是直角吗?请说明理由.
21.(8分)一轮船在大海中航行,先向正北方向航行8
km,接着转向正东方向航行15
km.
(1)此时轮船离出发点多少千米?
(2)若轮船每航行1
km需耗油0.4升,在此过程中轮船共耗油多少升?
22.(8分)有一根长30
cm的木棒,现要从木棒截下3段,做一个直角三角形的模具,可以怎样截取(允许有余料)?请设计出两种不同的方案.
23.(8分)某住宅小区有一块草坪如图11所示.已知AB=3
m,BC=4
m,CD=12
m,DA=13
m,且AB⊥BC,求这块草坪的面积.
24.(9分)如图12,一个长方体盒子的宽AN=5
cm,长ND=10
cm,CD边上有一点B到点D的距离为8
cm,若地面A处的一只蚂蚁到B处吃食,需要爬行的最短距离是多少?
25.(9分)如图13,一幢居民楼与马路平行且相距9
m,在距离载重汽车41
m处(图中点B的位置)就会受到噪音影响,试求在马路上以4
m/s的速度行驶的载重汽车,给这幢居民楼一楼的居民带来多长时间的噪音影响?若影响时间超过25
s,则此路禁止该车通行,那么载重汽车可以在这条路上通行吗?(点A代表居民楼)
26.(10分)张老师在一次“探究学习”课中,设计了下表:
2
3
4
5
…
…
4
6
8
10
…
…
(1)请你分别观察,,与之间的关系,并用含自然数()的代数式表示:______,______,_________;
(2)以,,为边的三角形是直角三角形吗?请说明理由.
参考答案:
一、1.C
2.D
3.C
4.D
5.B
6.C
7.B
8.A
9.B
10.D
二、11.6
12.不垂直
13.8
14.25
15.480
16.4.8
17.11,60,61
18.15
三、19.解:由勾股定理,得(x+4)2=36+x2,解得x=,所以S△ABC
=×6×=.
20.解:∠ACB是直角.
理由:因为BC2=22+42=20,AC2=12+22=5,AB2=32+42=25,所以AB2=
BC2+AC2.所以△ABC是直角三角形,且∠ACB=90°.
21.
解:(1)根据题意,画出图形(如图1所示).
由图可知AB=8
km,BC=15
km.
在Rt△ABC中,由勾股定理,得AC2=82+152=172,即AC=17.所以此时轮船离出点17
km.
(2)(8+15)×0.4=23×0.4=9.2(升).
答:在此过程中轮船共耗油9.2升.
22.解:答案不唯一,给出两种方案供参考.
方案一
:分别截取6
cm,8
cm,10
cm.因为62+82=102,所以以6
cm,8
cm,10
cm为边的三角形是直角三角形,可以做一个直角三角形模具;
方案二:分别截取5
cm,12
cm,13
cm.因为52+122=132,所以以5
cm,12
cm,13
cm为边的三角形是直角三角形,可以做一个直角三角形模具.
23.
解:连接AC.
因为AB⊥BC,所以∠B=90°.在Rt△ABC中,AB=3
m,BC=4
m,由勾股定理,得AC=5
m.
在△ACD中,AC2+CD2=52+122=169=AD2,所以△ACD为直角三角形.
所以草坪的面积=S△ABC+S△ACD=×3×4+×5×12=6+30=36(m
2).
24.
解:将长方体盒子的侧面展开(如图2所示),连接AB,则AB的长即为A处到B处的最短距离.
在Rt△ABD中,AD=AN+ND=5+10=15(cm),BD=8
cm,所以AB2=AD2+BD2=152+82=289=172,即AB=17
cm.所以蚂蚁爬行的最短距离为17
cm.
25.解:如图3所示,由题意,知AB=AD=41
m,AC=9
m.
在Rt△ABC中,BC2=AB2-AC2=412-92=402,即BC=40
m
.所以BD=2BC=2×40=80
m
.
因为=20
s,所以该车给居民带来20
s的噪音影响.
因为带来噪音影响的时间小于25
s,所以该载重汽车可以在这条路上通行.
26.解:(1)
(2)以,,为边的三角形是直角三角形.
理由:因为a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1,所以a2+b2=c2.
所以以a,b,c为边的三角形是直角三角形.
图1
60
m
80
m
C
D
B
A
图2
图7
C
C'
B
A
图6
图8
A
蚂蚁
C
蜂蜜
图5
图10
C
B
A
图9
图11
E
M
C
N
D
B
A
图12
图13
北
C
B
A
图1
E
M
C
N
D
B
A
图2
图3
勾股定理综合测评
(时间:
满分:120分)
(班级:
姓名:
得分:
)
一、精心选一选(每小题3分,共30分)
1.下列各组线段中,能构成直角三角形的是( )
A.
4,5,6
B.,,
C.
1,,
D.
4,6,8
2.
下列各组数中,是勾股数的是(
)
A.
2,3,4
B.
6,8,9
C.
5,11,13
D.
9,40,41
3.图1所示是某学校的长方形操场,如果一学生要从操场A角走到C角,至少要走( )
A.140
m
B.120
m
C.100
m
D.90
m
图1
图2
图3
4.下列说法正确的是( )
A.若a,b,c是△ABC的三边长,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边长,∠B=90°,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边长,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边长,∠C=90°,则a2+b2=c2
5.已知等腰三角形的腰长为10
cm,底边长为16
cm,则这个等腰三角形的面积为( )
A.96
cm2
B.48
cm2
C.24
cm2
D.32
cm2
6.一个直角三角形的两条边长分别是9和12,则第三边的平方是( )
A.225
B.441
C.63或225
D.63
7.某中学旁边有一块三角形空地,为了保持水土,美化环境,全校师生齐动手,在空地的三条边上栽上了树苗(如图2所示).已知三边上的树苗数分别为56,49,74,空地的三个角均有一棵树,且每条边上的树苗株距(相邻两树苗间的距离)均为1
m,那么这块空地的形状为( )
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
不能确定
8.一艘小船早上8:00从港口出发,以8海里/时的速度向东航行,1小时后,另一艘小船以12海里/时的速度由同一港口出发向南航行,到上午10:00两艘小船相距( )
A.
20海里
B.
15海里
C.
13海里
D.
12海里
9.图3中所有三角形都是直角三角形,所有四边形都是正方形.已知S1
,S2,S3,S4,S分别表示所在正方形的面积,若S1=4,S2=9,S3=8,S4=10,则S的值为( )
A.25
B.31
C.32
D.40
10.图4所示是验证勾股定理采用的一种图形,其中两个全等的直角三角形边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.
B.
图4
C.
D.
二、细心填一填(每小题3分,共24分)
11.在△ABC中,∠C=90°,AB=10,BC=8,则AC的长为________.
12.一根电线杆高8
m,为了安全起见,工人师傅在电线杆顶部到与电线杆底部水平距离6
m处加了一根拉线,发现所用拉线长为10.3
m(不计捆绑部分),则电线杆与地面__________(填“垂直”或“不垂直”).
13.
在Rt△ABC中,已知斜边AB的长为2,则AB2+BC2+CA2=
.
14.图5所示阴影部分的面积x=_________.
15.如图6,某人欲从A点横渡一条河,受水流的影响,实际上岸地点C与欲到达点B偏离了200
m,他在水中实际游了520
m,则该河流的宽度为_______m.
16.
如图7,在△ABC中,AC=3,BC=4,AB=5,将△ABC沿AB翻折到△ABC',则CC'的长度是___________.
17.观察下列几组勾股数,并寻找规律:
①3,4,5;②5,12,13;③7,24,25;④9,40,41;…
根据上面的规律,写出第⑤组勾股数:_______________.
18.如图8,圆柱形玻璃杯高为12
cm、底面周长为18
cm,在杯内离杯底4
cm的C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4
cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离为______cm.
三、耐心做一做(共66分)
19.(6分)求图9所示△ABC的面积.
20.(8分)如图10,在5×5的方格纸中,每一个小正方形的边长都为1,∠ACB是直角吗?请说明理由.
21.(8分)一轮船在大海中航行,先向正北方向航行8
km,接着转向正东方向航行15
km.
(1)此时轮船离出发点多少千米?
(2)若轮船每航行1
km需耗油0.4升,在此过程中轮船共耗油多少升?
22.(8分)有一根长30
cm的木棒,现要从木棒截下3段,做一个直角三角形的模具,可以怎样截取(允许有余料)?请设计出两种不同的方案.
23.(8分)某住宅小区有一块草坪如图11所示.已知AB=3
m,BC=4
m,CD=12
m,DA=13
m,且AB⊥BC,求这块草坪的面积.
24.(9分)如图12,一个长方体盒子的宽AN=5
cm,长ND=10
cm,CD边上有一点B到点D的距离为8
cm,若地面A处的一只蚂蚁到B处吃食,需要爬行的最短距离是多少?
25.(9分)如图13,一幢居民楼与马路平行且相距9
m,在距离载重汽车41
m处(图中点B的位置)就会受到噪音影响,试求在马路上以4
m/s的速度行驶的载重汽车,给这幢居民楼一楼的居民带来多长时间的噪音影响?若影响时间超过25
s,则此路禁止该车通行,那么载重汽车可以在这条路上通行吗?(点A代表居民楼)
26.(10分)张老师在一次“探究学习”课中,设计了下表:
2
3
4
5
…
…
4
6
8
10
…
…
(1)请你分别观察,,与之间的关系,并用含自然数()的代数式表示:______,______,_________;
(2)以,,为边的三角形是直角三角形吗?请说明理由.
参考答案:
一、1.C
2.D
3.C
4.D
5.B
6.C
7.B
8.A
9.B
10.D
二、11.6
12.不垂直
13.8
14.25
15.480
16.4.8
17.11,60,61
18.15
三、19.解:由勾股定理,得(x+4)2=36+x2,解得x=,所以S△ABC
=×6×=.
20.解:∠ACB是直角.
理由:因为BC2=22+42=20,AC2=12+22=5,AB2=32+42=25,所以AB2=
BC2+AC2.所以△ABC是直角三角形,且∠ACB=90°.
21.
解:(1)根据题意,画出图形(如图1所示).
由图可知AB=8
km,BC=15
km.
在Rt△ABC中,由勾股定理,得AC2=82+152=172,即AC=17.所以此时轮船离出点17
km.
(2)(8+15)×0.4=23×0.4=9.2(升).
答:在此过程中轮船共耗油9.2升.
22.解:答案不唯一,给出两种方案供参考.
方案一
:分别截取6
cm,8
cm,10
cm.因为62+82=102,所以以6
cm,8
cm,10
cm为边的三角形是直角三角形,可以做一个直角三角形模具;
方案二:分别截取5
cm,12
cm,13
cm.因为52+122=132,所以以5
cm,12
cm,13
cm为边的三角形是直角三角形,可以做一个直角三角形模具.
23.
解:连接AC.
因为AB⊥BC,所以∠B=90°.在Rt△ABC中,AB=3
m,BC=4
m,由勾股定理,得AC=5
m.
在△ACD中,AC2+CD2=52+122=169=AD2,所以△ACD为直角三角形.
所以草坪的面积=S△ABC+S△ACD=×3×4+×5×12=6+30=36(m
2).
24.
解:将长方体盒子的侧面展开(如图2所示),连接AB,则AB的长即为A处到B处的最短距离.
在Rt△ABD中,AD=AN+ND=5+10=15(cm),BD=8
cm,所以AB2=AD2+BD2=152+82=289=172,即AB=17
cm.所以蚂蚁爬行的最短距离为17
cm.
25.解:如图3所示,由题意,知AB=AD=41
m,AC=9
m.
在Rt△ABC中,BC2=AB2-AC2=412-92=402,即BC=40
m
.所以BD=2BC=2×40=80
m
.
因为=20
s,所以该车给居民带来20
s的噪音影响.
因为带来噪音影响的时间小于25
s,所以该载重汽车可以在这条路上通行.
26.解:(1)
(2)以,,为边的三角形是直角三角形.
理由:因为a2+b2=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1,所以a2+b2=c2.
所以以a,b,c为边的三角形是直角三角形.
图1
60
m
80
m
C
D
B
A
图2
图7
C
C'
B
A
图6
图8
A
蚂蚁
C
蜂蜜
图5
图10
C
B
A
图9
图11
E
M
C
N
D
B
A
图12
图13
北
C
B
A
图1
E
M
C
N
D
B
A
图2
图3
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
