数学六年级下西师大版5统计与概率导学案
文档属性
| 名称 | 数学六年级下西师大版5统计与概率导学案 | 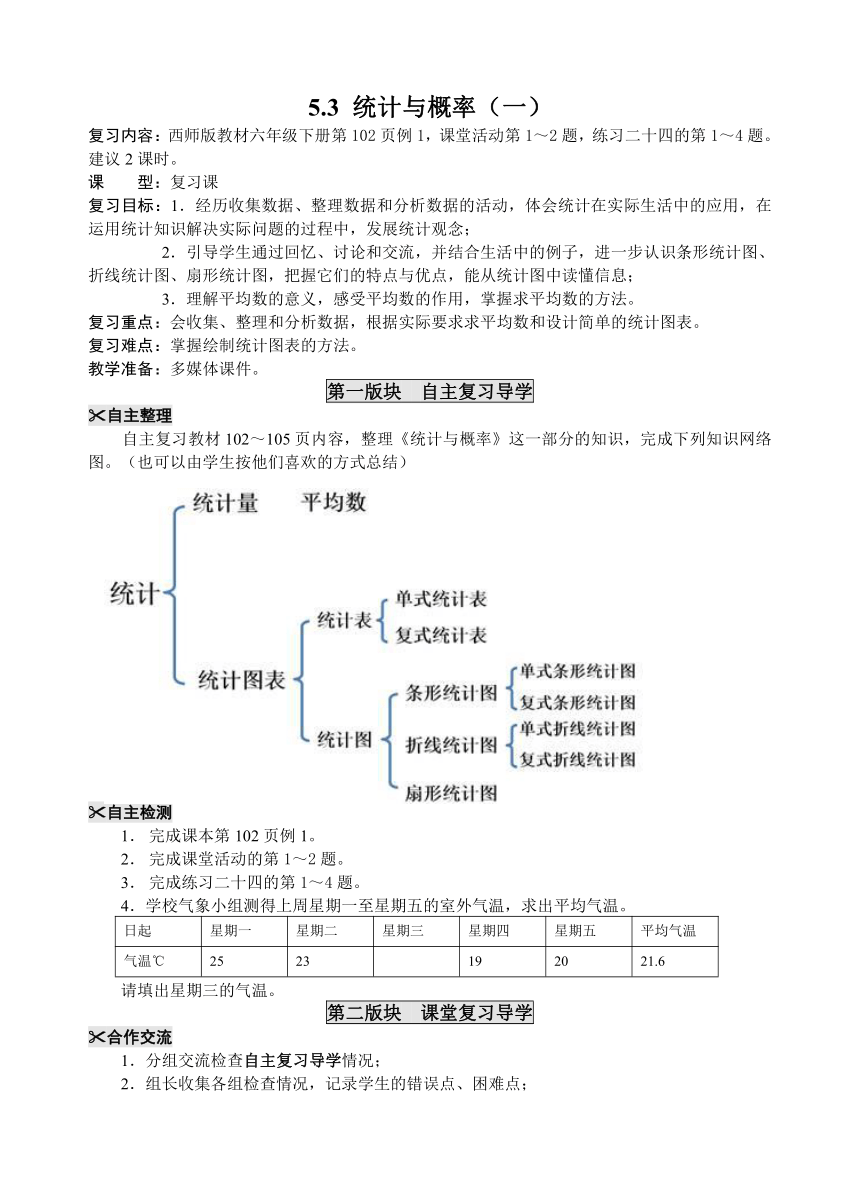 | |
| 格式 | zip | ||
| 文件大小 | 178.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-12 18:44:09 | ||
图片预览


文档简介
5.3
统计与概率(一)
复习内容:西师版教材六年级下册第102页例1,课堂活动第1~2题,练习二十四的第1~4题。建议2课时。
课
型:复习课
复习目标:1.经历收集数据、整理数据和分析数据的活动,体会统计在实际生活中的应用,在运用统计知识解决实际问题的过程中,发展统计观念;
2.引导学生通过回忆、讨论和交流,并结合
( http: / / www.21cnjy.com )生活中的例子,进一步认识条形统计图、折线统计图、扇形统计图,把握它们的特点与优点,能从统计图中读懂信息;
3.理解平均数的意义,感受平均数的作用,掌握求平均数的方法。
复习重点:会收集、整理和分析数据,根据实际要求求平均数和设计简单的统计图表。
复习难点:掌握绘制统计图表的方法。
教学准备:多媒体课件。
第一版块
自主复习导学
自主整理
自主复习教材102~105页内容,整理《统计与概率》这一部分的知识,完成下列知识网络图。(也可以由学生按他们喜欢的方式总结)
自主检测
完成课本第102页例1。
完成课堂活动的第1~2题。
完成练习二十四的第1~4题。
4.学校气象小组测得上周星期一至星期五的室外气温,求出平均气温。
日起
星期一
星期二
星期三
星期四
星期五
平均气温
气温℃
25
23
19
20
21.6
请填出星期三的气温。
第二版块
课堂复习导学
合作交流
1.分组交流检查自主复习导学情况;
2.组长收集各组检查情况,记录学生的错误点、困难点;
3.教师巡视、指导、帮助,收集错误点、困难点,优秀的学生作品,以备展示。
展示点拨
1.教师组织学生展示,并点拨。
2.统计表分类及制作步骤。
3.统计活动中经历了哪些过程?(提出问题、收集数据、整理数据、分析数据、作出决策)
4.常用的统计图有
(
)统计图,
(
)统计图和
(
)统计图。
5.各种统计图的特点和作用。
条形统计图
折线统计图
扇形统计图
特点
用一个单位长表示相同数量
用整个圆的面积表示总数量,用圆内各扇形的面积表示各部分数量占总量的百分数
用直条长度表示数量多少
用折线的起伏表示数量增减的变化
作用
能清楚地反映出数量的多少,便于数量间的比较
不仅能清楚地反映出数量的多少,而且能反映出数量的变化的趋势
能清楚地反映出各部分数量占总量的百分之几,以及各部分数量之间关系。
6.平均数
=
一组数据的总和
÷
这组数据的个数。
分层训练
(一)巩固练习
1.填空题:
(1)商业大厦电梯的载重限额是1250千克,那么电梯最多可以运送(
)个75千克的人而不超载。
(2)医生想用统计图记录病人24小时的体温变化情况,他选用(
)统计图比较合适。
(3)要表示本校三至六年级各年级的人数,用(
)统计图表示比较合适。
(4)根据统计图填空
东风机械厂2012年全年产值统计图
①平均每个季度产值(
)万元。
②全年平均每月产值约(
)万元。
③第四季度比第一季度增产(
)%。
④第三季度比第四季度少产(
)%。
⑤下半年的产值占全年产值的(
)%。
(二)课堂检测
1.判断题。正确的在(
)打“√”,错误的在(
)打“×”
。
(1)体检时学生的体重记录是一份原始数据单。
(
)
为了清楚地表示各个课外兴趣小组人数的多少,选用扇形统计图比较合适。(
)
(2).画线条统计图时,应该注意直条的宽窄必须一样。
(
)
(3)用统计表表示的数量不能用统计图表示。
(
)
2.选择题。
(1)省疾控中心为做好甲型H1N1流感防控
( http: / / www.21cnjy.com )工作,每天都进行疫情统计。既反映出每天患病人数,又反映出疫情变化的情况和趋势,他们应选用(
)统计图。
A
条形
B
折线
C
扇形
(2)下面的信息资料中,适合用扇形统计图表示的是(
)
A
学校各年纪的人数
B
6月份气温变化情况
C
学校各年纪学生人数占学生总数的情况
(3)为了清楚地表示出数量的多少,常用(
( http: / / www.21cnjy.com )
)统计图;为了表示出数量的增减变化情况,用(
)统计图比较合适;而(
)统计图却能清楚地表示出部分量与总体的关系。
A.条形统计图
B.折线统计图
C.扇形统计图
3.根据下面的统计图。
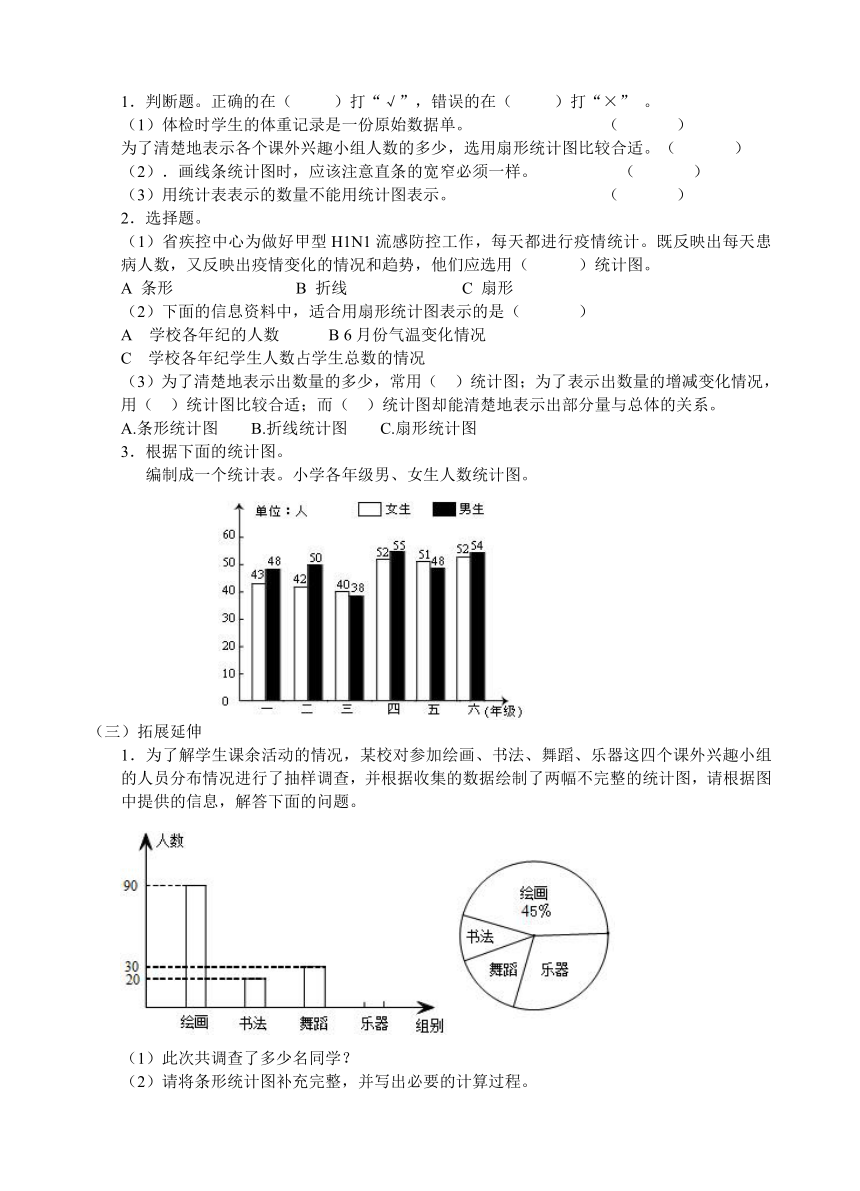
编制成一个统计表。小学各年级男、女生人数统计图。
(三)拓展延伸
1.为了解学生课余活动的情
( http: / / www.21cnjy.com )况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行了抽样调查,并根据收集的数据绘制了两幅不完整的统计图,请根据图中提供的信息,解答下面的问题。
(1)此次共调查了多少名同学?
(2)请将条形统计图补充完整,并写出必要的计算过程。
(3)如果该校共有1000名学生参加了这4个课外兴趣小组,而每个小时最多只能辅导本组的20名学生,那么舞蹈小组至少需要安排多少位老师?
反思总结
统计表概念、分类、制作步骤;
各种统计图的特点与作用;
统计表与统计图的综合运用
求平均数的方法。
5.3
统计与概率(二)
复习内容:西师版教材六年级下册第103页例2,课堂活动第3题,练习二十四的第5~9题。建议2课时。
课
型:复习课
复习目标:1.进一步体会事件发生的可能性的含义,知道可能性是有大小的,会用分数表示一些简单事件发生的可能性大小;
2.进一步体会游戏规则的公平性,能判断简单游戏是否公平,能设计简单的公平游戏规则;
3.经历整理“可能性”知识的过程,培养学生分析、归纳的能力。
复习重点:复习可能性的相关知识。
复习难点:运用可能性的知识解答一些实际问题。
教学准备:多媒体课件。
第一版块
自主复习导学
自主整理
自主复习教材103~104页内容,整理《统计与概率》这一部分的知识,完成下列知识网络图。(也可以由学生按他们喜欢的方式总结)
一定
大
确定
不确定——可能
相等——游戏规则公平
不可能
小
自主检测
完成教材第103页的例2。
完成课堂活动的第2题。
完成练习二十四的第5~9题。
(设计本单元的基础知识复习题,用以检查
( http: / / www.21cnjy.com )学生自主复习情况及基础知识回顾掌握的情况。可以是教材上本单元基础题及改编题,也可以是练习二十四的题及改编题,还可以是新课学习中学生做错了的题等。题目要体现基础性、全面性、纠错性。)
第二版块
课堂复习导学
合作交流
1.分组交流检查自主复习导学情况;
2.组长收集各组检查情况,记录学生的错误点、困难点;
3.教师巡视、指导、帮助,收集错误点、困难点,优秀的学生作品,以备展示。
展示点拨
1.可能性分为(能确定的)和(不能确定的)两种。
2.可能性大小的求法:可能性大小=
( http: / / www.21cnjy.com )事件发生的可能的结果数÷所有可能的结果总数,即可能性就是用一定能出现的次数与可能出现所有次数的最简整数比。
3.表示一个事件发生的可能性大小的数,叫做该事件的概率。
它是随机事件出现的可能性的量度,同
( http: / / www.21cnjy.com )时也是概率论最基本的概念之一。人们常说某人有百分之多少的把握能通过这次考试,某件事发生的可能性是多少,这都是概率的实列。但如果一件事情发生的概率是1/n
,不是指n次事件里必有一次发生该事件,而是指此事件发生的概率接近于1/n这个数值。
游戏的公平性。
游戏规则必须保证事件发生的可能性相等,这样游
( http: / / www.21cnjy.com )戏才公平。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方发生的可能性是否相等。若相等,游戏公平;若不相等,游戏不公平。
分层训练
(围绕本单元的基础知识点、重点、难点、易错点等,设计3个层次即巩固练习、课堂检测、拓展延伸的训练题。注意要体现层次性,针对性。)
(一)巩固练习
1.填空题:
(1)抛出一枚硬币,落下后有(
)种结果。出现反而的可能性有(
)
(2)李明和高飞下跳棋,他们用掷骰子的方式决定谁走几步,骰子各面分别写着1、2、3、4、5、6,抛出每个数字的可能性是(
)。
(3)一个装满白球的盒子里,(
)摸出红球,(
)摸出白球。
(4)商业大厦电梯的载重限额是1250千克,那么电梯最多可以运送(
)个75千克的人而不超载。
(5)桌子上摆着9张卡片,
( http: / / www.21cnjy.com )分别写着1~9各数。如果摸着单数小明赢,如果摸着双数小红赢。这个游戏公平吗?小红一定会赢吗?你能设计一个公平的游戏规则吗?
(二)课堂检测
1.判断题。正确的在(
)打“√”,错误的在(
)打“×”
。
(1)一种彩票中奖率为1%,小明买100张有一张一定中奖。
(
)
(2)成语“水中捞月”描述的事件是不可能发生的。(
)
(3)掷硬币10次,恰好出现5次正面朝上,5次反面朝上。
(
)
(4)可能性很大的事件就是一定会发生的事件。
(
)
(5)小明的身高是1.4米,在平均水深1.2米的游泳池中游泳没有危险。(
)
2.选择题。
(1)两个骰子同时掷一次,下面说法正确的是(
)。
A
两个数的和不可能是1
B
两个数的和可能是13
C两个数的和可能是1~12
(2)如图,转动转盘,转盘停止转动时指针指向(
)区域的可能性最小。
A黄色
B
红色
C蓝色
(3)六(一)班同学到社
( http: / / www.21cnjy.com )区参加公益活动,社区主任问班长出勤的情况,班长说:“我们班共有50人,没有全部到齐,但大部分来了。”出勤率可能是(
)。
A
50%
B
48%
C
96%
(4)某地的天气预报中说:“明天的降水概率中80%。”根据这个预报,下面说法正确的是(
)
A
明天一定下雨
B
明天不可能下雨
C
明天下雨的可能性很大
(三)拓展延伸
一个箱子中放有红、黄、黑三个小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢,这个游戏公平吗?为什么?
反思总结
可能性的概念;
数学中的可能性;
游戏的公平性。
5.3
王老师买新房
学习内容:西师版教材六年级下册第107页。
课型:综合实践课
学习目标: 利用数与代数中常见的数量关
( http: / / www.21cnjy.com )系,利息计算及空间与图形中面积计算等知识解决生活问题。发展学生综合应用知识解决问题的能力。
学习重点和难点 :让学生综合应用知识解决问题的能力,进一步巩固有关知识。
教具准备:多媒体
教学过程:
情景创设 :
王老师买了一套新方,让我们来看看,买房时提供的一些信息,从中你能提出哪些数学问题?
学生自主提问,独立解答。
启发学生思考问题。
解决问题 :
一、王老师的新房面积是多少平方米?
(长方形、圆的组合图形的面积。)
(一
( http: / / www.21cnjy.com )) 两间卧室+客厅+阳台的一半
3×(4+2)+5×(3+3)+5×(5+3)+3.14×2×2÷2÷2=91.4(㎡)
(二) 大长方形+半圆面积的一半。
(3+3+5)×(5+3)+3.14×2×2÷2÷2=91.4(㎡)。
二、王老师要向银行贷款多少元?平均每月还款多少元?
(利息)
以第一问中计算出来的面积为条件,算
( http: / / www.21cnjy.com )出购买新房的总价,并减去首付款后就是要向银行贷的款。即1800×91.4-44052=120000元;平均每月还款多少元?应用贷款本金+利息,再除以240月。即(120000+120000×5.04%×20)÷240=1004元。
三、王老师如果选用规格为50㎝×50㎝,每块单价15元的地砖扑地面(需要铺砖的面积约占总面积的85%),购买地砖要多少元?
(正方形的面积、单价、数量与总价的关系)
实际需要地砖的块数×单价
91.4×85%÷(0.5×0.5)×15=4648.14(元)
四、王老师准备给两间卧室的内墙壁(两个窗户和两扇门的面积大约10㎡)和房顶涂上乳胶漆,乳胶漆按5元/㎡计算,买乳胶漆要多少元?
(表面积+常用的数量关系)
(卧室1表面
( http: / / www.21cnjy.com )积+卧室2表面积)×乳胶漆的单价
[(3+4)×2×2.85+3×4+(3+5)×2×2.85+3×5-10]×5=512.5(元) 学生有两种基本计算方法。1、把王老师的新房平面图可以分解成2间卧室(含卫生间)、客厅和阳台的面积。
2、把卧室、卫生间、客厅看成一个大的长方形直接计算再加上阳台的面积。
学生先小组内说清楚思路再解决。
训练学生会用不同的方法看图,从而采取
( http: / / www.21cnjy.com )不同的计算方法进行计算。
熟练掌握计算房屋贷款的方法。
能解决简单的房屋装修的方法。
三、你还能提出哪些数学问题?请提出来并解答。
黄
篮
红
统计与概率(一)
复习内容:西师版教材六年级下册第102页例1,课堂活动第1~2题,练习二十四的第1~4题。建议2课时。
课
型:复习课
复习目标:1.经历收集数据、整理数据和分析数据的活动,体会统计在实际生活中的应用,在运用统计知识解决实际问题的过程中,发展统计观念;
2.引导学生通过回忆、讨论和交流,并结合
( http: / / www.21cnjy.com )生活中的例子,进一步认识条形统计图、折线统计图、扇形统计图,把握它们的特点与优点,能从统计图中读懂信息;
3.理解平均数的意义,感受平均数的作用,掌握求平均数的方法。
复习重点:会收集、整理和分析数据,根据实际要求求平均数和设计简单的统计图表。
复习难点:掌握绘制统计图表的方法。
教学准备:多媒体课件。
第一版块
自主复习导学
自主整理
自主复习教材102~105页内容,整理《统计与概率》这一部分的知识,完成下列知识网络图。(也可以由学生按他们喜欢的方式总结)
自主检测
完成课本第102页例1。
完成课堂活动的第1~2题。
完成练习二十四的第1~4题。
4.学校气象小组测得上周星期一至星期五的室外气温,求出平均气温。
日起
星期一
星期二
星期三
星期四
星期五
平均气温
气温℃
25
23
19
20
21.6
请填出星期三的气温。
第二版块
课堂复习导学
合作交流
1.分组交流检查自主复习导学情况;
2.组长收集各组检查情况,记录学生的错误点、困难点;
3.教师巡视、指导、帮助,收集错误点、困难点,优秀的学生作品,以备展示。
展示点拨
1.教师组织学生展示,并点拨。
2.统计表分类及制作步骤。
3.统计活动中经历了哪些过程?(提出问题、收集数据、整理数据、分析数据、作出决策)
4.常用的统计图有
(
)统计图,
(
)统计图和
(
)统计图。
5.各种统计图的特点和作用。
条形统计图
折线统计图
扇形统计图
特点
用一个单位长表示相同数量
用整个圆的面积表示总数量,用圆内各扇形的面积表示各部分数量占总量的百分数
用直条长度表示数量多少
用折线的起伏表示数量增减的变化
作用
能清楚地反映出数量的多少,便于数量间的比较
不仅能清楚地反映出数量的多少,而且能反映出数量的变化的趋势
能清楚地反映出各部分数量占总量的百分之几,以及各部分数量之间关系。
6.平均数
=
一组数据的总和
÷
这组数据的个数。
分层训练
(一)巩固练习
1.填空题:
(1)商业大厦电梯的载重限额是1250千克,那么电梯最多可以运送(
)个75千克的人而不超载。
(2)医生想用统计图记录病人24小时的体温变化情况,他选用(
)统计图比较合适。
(3)要表示本校三至六年级各年级的人数,用(
)统计图表示比较合适。
(4)根据统计图填空
东风机械厂2012年全年产值统计图
①平均每个季度产值(
)万元。
②全年平均每月产值约(
)万元。
③第四季度比第一季度增产(
)%。
④第三季度比第四季度少产(
)%。
⑤下半年的产值占全年产值的(
)%。
(二)课堂检测
1.判断题。正确的在(
)打“√”,错误的在(
)打“×”
。
(1)体检时学生的体重记录是一份原始数据单。
(
)
为了清楚地表示各个课外兴趣小组人数的多少,选用扇形统计图比较合适。(
)
(2).画线条统计图时,应该注意直条的宽窄必须一样。
(
)
(3)用统计表表示的数量不能用统计图表示。
(
)
2.选择题。
(1)省疾控中心为做好甲型H1N1流感防控
( http: / / www.21cnjy.com )工作,每天都进行疫情统计。既反映出每天患病人数,又反映出疫情变化的情况和趋势,他们应选用(
)统计图。
A
条形
B
折线
C
扇形
(2)下面的信息资料中,适合用扇形统计图表示的是(
)
A
学校各年纪的人数
B
6月份气温变化情况
C
学校各年纪学生人数占学生总数的情况
(3)为了清楚地表示出数量的多少,常用(
( http: / / www.21cnjy.com )
)统计图;为了表示出数量的增减变化情况,用(
)统计图比较合适;而(
)统计图却能清楚地表示出部分量与总体的关系。
A.条形统计图
B.折线统计图
C.扇形统计图
3.根据下面的统计图。
编制成一个统计表。小学各年级男、女生人数统计图。
(三)拓展延伸
1.为了解学生课余活动的情
( http: / / www.21cnjy.com )况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行了抽样调查,并根据收集的数据绘制了两幅不完整的统计图,请根据图中提供的信息,解答下面的问题。
(1)此次共调查了多少名同学?
(2)请将条形统计图补充完整,并写出必要的计算过程。
(3)如果该校共有1000名学生参加了这4个课外兴趣小组,而每个小时最多只能辅导本组的20名学生,那么舞蹈小组至少需要安排多少位老师?
反思总结
统计表概念、分类、制作步骤;
各种统计图的特点与作用;
统计表与统计图的综合运用
求平均数的方法。
5.3
统计与概率(二)
复习内容:西师版教材六年级下册第103页例2,课堂活动第3题,练习二十四的第5~9题。建议2课时。
课
型:复习课
复习目标:1.进一步体会事件发生的可能性的含义,知道可能性是有大小的,会用分数表示一些简单事件发生的可能性大小;
2.进一步体会游戏规则的公平性,能判断简单游戏是否公平,能设计简单的公平游戏规则;
3.经历整理“可能性”知识的过程,培养学生分析、归纳的能力。
复习重点:复习可能性的相关知识。
复习难点:运用可能性的知识解答一些实际问题。
教学准备:多媒体课件。
第一版块
自主复习导学
自主整理
自主复习教材103~104页内容,整理《统计与概率》这一部分的知识,完成下列知识网络图。(也可以由学生按他们喜欢的方式总结)
一定
大
确定
不确定——可能
相等——游戏规则公平
不可能
小
自主检测
完成教材第103页的例2。
完成课堂活动的第2题。
完成练习二十四的第5~9题。
(设计本单元的基础知识复习题,用以检查
( http: / / www.21cnjy.com )学生自主复习情况及基础知识回顾掌握的情况。可以是教材上本单元基础题及改编题,也可以是练习二十四的题及改编题,还可以是新课学习中学生做错了的题等。题目要体现基础性、全面性、纠错性。)
第二版块
课堂复习导学
合作交流
1.分组交流检查自主复习导学情况;
2.组长收集各组检查情况,记录学生的错误点、困难点;
3.教师巡视、指导、帮助,收集错误点、困难点,优秀的学生作品,以备展示。
展示点拨
1.可能性分为(能确定的)和(不能确定的)两种。
2.可能性大小的求法:可能性大小=
( http: / / www.21cnjy.com )事件发生的可能的结果数÷所有可能的结果总数,即可能性就是用一定能出现的次数与可能出现所有次数的最简整数比。
3.表示一个事件发生的可能性大小的数,叫做该事件的概率。
它是随机事件出现的可能性的量度,同
( http: / / www.21cnjy.com )时也是概率论最基本的概念之一。人们常说某人有百分之多少的把握能通过这次考试,某件事发生的可能性是多少,这都是概率的实列。但如果一件事情发生的概率是1/n
,不是指n次事件里必有一次发生该事件,而是指此事件发生的概率接近于1/n这个数值。
游戏的公平性。
游戏规则必须保证事件发生的可能性相等,这样游
( http: / / www.21cnjy.com )戏才公平。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方发生的可能性是否相等。若相等,游戏公平;若不相等,游戏不公平。
分层训练
(围绕本单元的基础知识点、重点、难点、易错点等,设计3个层次即巩固练习、课堂检测、拓展延伸的训练题。注意要体现层次性,针对性。)
(一)巩固练习
1.填空题:
(1)抛出一枚硬币,落下后有(
)种结果。出现反而的可能性有(
)
(2)李明和高飞下跳棋,他们用掷骰子的方式决定谁走几步,骰子各面分别写着1、2、3、4、5、6,抛出每个数字的可能性是(
)。
(3)一个装满白球的盒子里,(
)摸出红球,(
)摸出白球。
(4)商业大厦电梯的载重限额是1250千克,那么电梯最多可以运送(
)个75千克的人而不超载。
(5)桌子上摆着9张卡片,
( http: / / www.21cnjy.com )分别写着1~9各数。如果摸着单数小明赢,如果摸着双数小红赢。这个游戏公平吗?小红一定会赢吗?你能设计一个公平的游戏规则吗?
(二)课堂检测
1.判断题。正确的在(
)打“√”,错误的在(
)打“×”
。
(1)一种彩票中奖率为1%,小明买100张有一张一定中奖。
(
)
(2)成语“水中捞月”描述的事件是不可能发生的。(
)
(3)掷硬币10次,恰好出现5次正面朝上,5次反面朝上。
(
)
(4)可能性很大的事件就是一定会发生的事件。
(
)
(5)小明的身高是1.4米,在平均水深1.2米的游泳池中游泳没有危险。(
)
2.选择题。
(1)两个骰子同时掷一次,下面说法正确的是(
)。
A
两个数的和不可能是1
B
两个数的和可能是13
C两个数的和可能是1~12
(2)如图,转动转盘,转盘停止转动时指针指向(
)区域的可能性最小。
A黄色
B
红色
C蓝色
(3)六(一)班同学到社
( http: / / www.21cnjy.com )区参加公益活动,社区主任问班长出勤的情况,班长说:“我们班共有50人,没有全部到齐,但大部分来了。”出勤率可能是(
)。
A
50%
B
48%
C
96%
(4)某地的天气预报中说:“明天的降水概率中80%。”根据这个预报,下面说法正确的是(
)
A
明天一定下雨
B
明天不可能下雨
C
明天下雨的可能性很大
(三)拓展延伸
一个箱子中放有红、黄、黑三个小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢,这个游戏公平吗?为什么?
反思总结
可能性的概念;
数学中的可能性;
游戏的公平性。
5.3
王老师买新房
学习内容:西师版教材六年级下册第107页。
课型:综合实践课
学习目标: 利用数与代数中常见的数量关
( http: / / www.21cnjy.com )系,利息计算及空间与图形中面积计算等知识解决生活问题。发展学生综合应用知识解决问题的能力。
学习重点和难点 :让学生综合应用知识解决问题的能力,进一步巩固有关知识。
教具准备:多媒体
教学过程:
情景创设 :
王老师买了一套新方,让我们来看看,买房时提供的一些信息,从中你能提出哪些数学问题?
学生自主提问,独立解答。
启发学生思考问题。
解决问题 :
一、王老师的新房面积是多少平方米?
(长方形、圆的组合图形的面积。)
(一
( http: / / www.21cnjy.com )) 两间卧室+客厅+阳台的一半
3×(4+2)+5×(3+3)+5×(5+3)+3.14×2×2÷2÷2=91.4(㎡)
(二) 大长方形+半圆面积的一半。
(3+3+5)×(5+3)+3.14×2×2÷2÷2=91.4(㎡)。
二、王老师要向银行贷款多少元?平均每月还款多少元?
(利息)
以第一问中计算出来的面积为条件,算
( http: / / www.21cnjy.com )出购买新房的总价,并减去首付款后就是要向银行贷的款。即1800×91.4-44052=120000元;平均每月还款多少元?应用贷款本金+利息,再除以240月。即(120000+120000×5.04%×20)÷240=1004元。
三、王老师如果选用规格为50㎝×50㎝,每块单价15元的地砖扑地面(需要铺砖的面积约占总面积的85%),购买地砖要多少元?
(正方形的面积、单价、数量与总价的关系)
实际需要地砖的块数×单价
91.4×85%÷(0.5×0.5)×15=4648.14(元)
四、王老师准备给两间卧室的内墙壁(两个窗户和两扇门的面积大约10㎡)和房顶涂上乳胶漆,乳胶漆按5元/㎡计算,买乳胶漆要多少元?
(表面积+常用的数量关系)
(卧室1表面
( http: / / www.21cnjy.com )积+卧室2表面积)×乳胶漆的单价
[(3+4)×2×2.85+3×4+(3+5)×2×2.85+3×5-10]×5=512.5(元) 学生有两种基本计算方法。1、把王老师的新房平面图可以分解成2间卧室(含卫生间)、客厅和阳台的面积。
2、把卧室、卫生间、客厅看成一个大的长方形直接计算再加上阳台的面积。
学生先小组内说清楚思路再解决。
训练学生会用不同的方法看图,从而采取
( http: / / www.21cnjy.com )不同的计算方法进行计算。
熟练掌握计算房屋贷款的方法。
能解决简单的房屋装修的方法。
三、你还能提出哪些数学问题?请提出来并解答。
黄
篮
红
