鲁教版数学八年级上册单元检测第四章 图形的平移与旋转综合测评
文档属性
| 名称 | 鲁教版数学八年级上册单元检测第四章 图形的平移与旋转综合测评 |  | |
| 格式 | zip | ||
| 文件大小 | 286.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-13 08:09:34 | ||
图片预览


文档简介
第四章
图形的平移与旋转综合测评
时间:
满分:120分
班级:
姓名:
得分:
一、选择题(每小题4分,共32分)
1.下列运动属于平移的是(
)
A.冷水加热过程中小气泡上升为大气泡
B.
随手抛出的彩球的运动
C.急刹车时汽车在地面上的滑动
D.
随风飘动的风筝在空中的运动
2.从5点15分到5点20分,分针旋转的度数为(
)
A.20°
B.26°
C.30°
D.36°
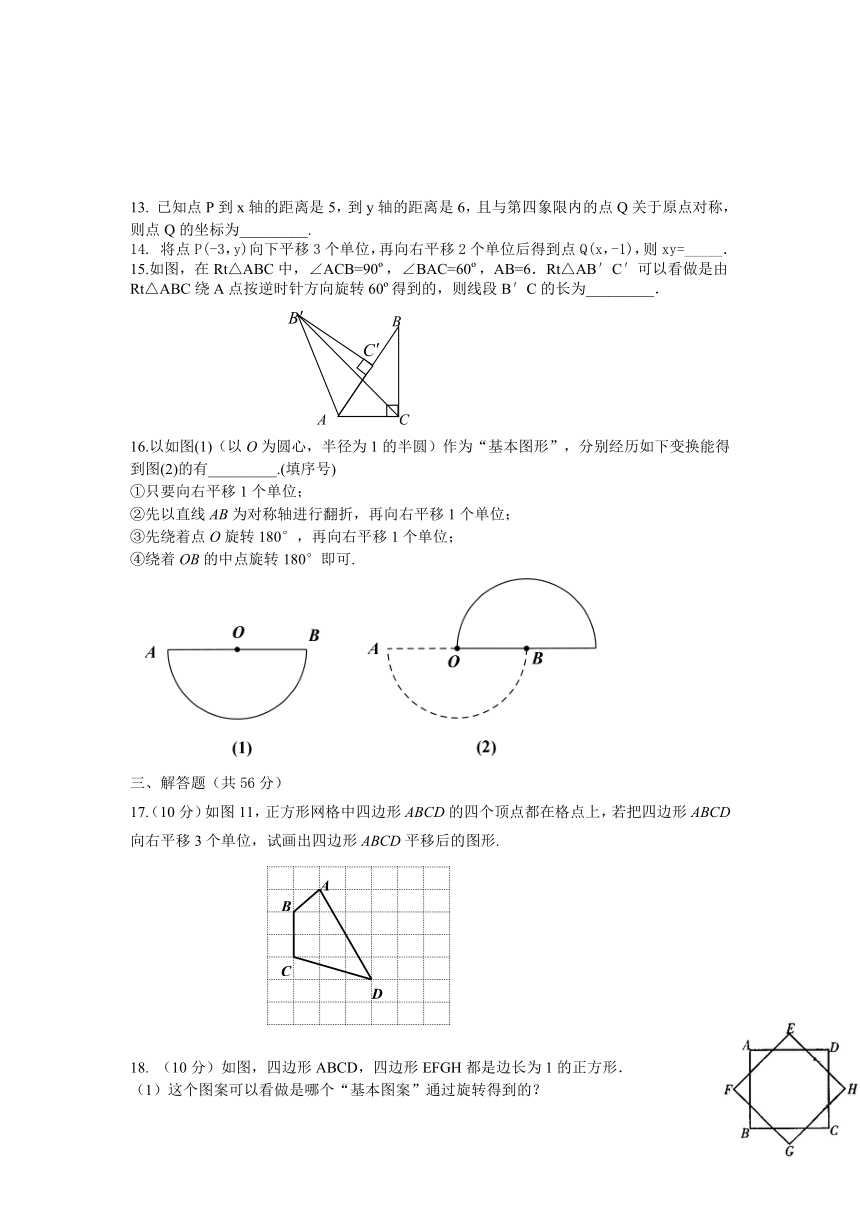
3.如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,可得点A的对应点A′的坐标是( )
A.(6,1)
B.(0,1)
C.(0,-3)
D.(6,-3)
4.
如图,将△ABC绕点C按顺时针方向旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则
∠BCA′的度数是( )
A.
30°
B.
40°
C.
80°
D.
110°
5.如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
A.把△ABC绕点C按逆时针方向旋转90°,再向下平移2格
B.把△ABC绕点C按顺时针方向旋转90°,再向下平移5格
C.把△ABC向下平移4格,再绕点C按逆时针方向旋转180°
D.把△ABC向下平移5格,再绕点C按顺时针方向旋转180°
6.在图所示的四个图案中,既可以用旋转来分析整个图案的形成过程,又可以用轴对称来分析整个图案的形成过程的图案有(
)
A.
1个
B.
2个
C.
3个
D.
4个
7.如图5,小红家楼梯长3
m,高2
m
,宽1
m,若想铺上地毯,则所需地毯的面积为(
)
A.
2
m2
B.3
m2
C.5
m2
D.6
m2
8.如图,△ABO中,AB⊥OB,
∠AOB=30 ,AB=1.把△ABO绕点O旋转90°后得到△A1B1O,则点A1的坐标为(
)
A.()
B.
()或()
C.()或()
D.
()
二、填空题(每小题4分,共32分)
9.下列现象:①转动的陀螺;②飞行中直升飞机的螺旋桨;③龙卷风;④流水线上的电视机.
属于平移的有___________.(填序号)
10.下面是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是_____.(填序号)
②
③
④
11.
如图,已知线段DE是由线段AB平移得到的,AB=4
cm,DC=2
cm,EC=4
cm,则△DCE的周长是________cm.
12.
如图,在△ABC中,AB=1.6,BC=3.6,∠B=60°,将△ABC绕点A按顺时针方向旋转一定的角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
.
13.
已知点P到x轴的距离是5,到y轴的距离是6,且与第四象限内的点Q关于原点对称,则点Q的坐标为_________.
14.
将点P(-3,y)向下平移3个单位,再向右平移2个单位后得到点Q(x,-1),则xy=_____.
15.如图,在Rt△ABC中,∠ACB=90 ,∠BAC=60 ,AB=6.Rt△AB′C′可以看做是由
Rt△ABC绕A点按逆时针方向旋转60 得到的,则线段B′C的长为_________.
16.以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换能得到图(2)的有_________.(填序号)
①只要向右平移1个单位;
②先以直线AB为对称轴进行翻折,再向右平移1个单位;
③先绕着点O旋转180°,再向右平移1个单位;
④绕着OB的中点旋转180°即可.
三、解答题(共56分)
17.(10分)如图11,正方形网格中四边形ABCD的四个顶点都在格点上,若把四边形ABCD向右平移3个单位,试画出四边形ABCD平移后的图形.
18.
(10分)如图,四边形ABCD,四边形EFGH都是边长为1的正方形.
(1)这个图案可以看做是哪个“基本图案”通过旋转得到的?
(2)旋转中心是什么?经过旋转,点A,B,C,D分别移到什么位置?
19.(12分)如图13,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)作出△ABC以点C为对称中心的图形△;
(2)平移△ABC,若点A对应点的坐标为(0,-4),画出平移后对应的△;
(3)若将△绕某一点旋转可以得到△,请直接写出旋转中心的坐标.
20.(12分)请你利用角、线段、平行线、三角形、正方形、圆、半圆等基本图案,借助平移、旋转或轴对称设计一个图案,并简述你的设计意图.
21.(12分)如图,已知P为正方形ABCD外的一点,PA=1,PB=2.将△ABP绕点B按顺时针方向旋转90°,使点P旋转至点P′,且AP′=3,求∠BP′C的度数.
参考答案
一、1.A
2.C
3.B
4.C
5.B
6.D
7.C
8.B
二、9.④
10.②
11.10
12.2
13.(6,-5)
14.-2
15.
16.
②③④
三、17.
图略.
18.
解:(1)可以看做是由正方形ABCD为“基础图案”按顺时针方向旋转45°得到正方形EFGH.
(2)旋转中心是AC与BD的交点.点A,点B,点C,点D分别移到了点E,点F,点G,点H.
19.
解:
(1)画出△如图1所示:
(2)画出△如图1所示:
(3)旋转中心的坐标为(,-1).
20.解:答案不唯一,如图2所示:
21.
解:连接PP′,由旋转的性质得P′B=PB=2,∠PBP′=90°.
所以PP′==2,∠BPP′=45°.
因为PA=1,AP′=3,所以PA2+PP′2=AP′2.
所以∠APP′=90°.
所以∠APB=∠APP′+∠BPP′=135°.
所以∠BP′C=∠APB=135°.
图5
A
C
B
A
B
CB
DCB
图2
图形的平移与旋转综合测评
时间:
满分:120分
班级:
姓名:
得分:
一、选择题(每小题4分,共32分)
1.下列运动属于平移的是(
)
A.冷水加热过程中小气泡上升为大气泡
B.
随手抛出的彩球的运动
C.急刹车时汽车在地面上的滑动
D.
随风飘动的风筝在空中的运动
2.从5点15分到5点20分,分针旋转的度数为(
)
A.20°
B.26°
C.30°
D.36°
3.如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,可得点A的对应点A′的坐标是( )
A.(6,1)
B.(0,1)
C.(0,-3)
D.(6,-3)
4.
如图,将△ABC绕点C按顺时针方向旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则
∠BCA′的度数是( )
A.
30°
B.
40°
C.
80°
D.
110°
5.如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
A.把△ABC绕点C按逆时针方向旋转90°,再向下平移2格
B.把△ABC绕点C按顺时针方向旋转90°,再向下平移5格
C.把△ABC向下平移4格,再绕点C按逆时针方向旋转180°
D.把△ABC向下平移5格,再绕点C按顺时针方向旋转180°
6.在图所示的四个图案中,既可以用旋转来分析整个图案的形成过程,又可以用轴对称来分析整个图案的形成过程的图案有(
)
A.
1个
B.
2个
C.
3个
D.
4个
7.如图5,小红家楼梯长3
m,高2
m
,宽1
m,若想铺上地毯,则所需地毯的面积为(
)
A.
2
m2
B.3
m2
C.5
m2
D.6
m2
8.如图,△ABO中,AB⊥OB,
∠AOB=30 ,AB=1.把△ABO绕点O旋转90°后得到△A1B1O,则点A1的坐标为(
)
A.()
B.
()或()
C.()或()
D.
()
二、填空题(每小题4分,共32分)
9.下列现象:①转动的陀螺;②飞行中直升飞机的螺旋桨;③龙卷风;④流水线上的电视机.
属于平移的有___________.(填序号)
10.下面是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是_____.(填序号)
②
③
④
11.
如图,已知线段DE是由线段AB平移得到的,AB=4
cm,DC=2
cm,EC=4
cm,则△DCE的周长是________cm.
12.
如图,在△ABC中,AB=1.6,BC=3.6,∠B=60°,将△ABC绕点A按顺时针方向旋转一定的角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
.
13.
已知点P到x轴的距离是5,到y轴的距离是6,且与第四象限内的点Q关于原点对称,则点Q的坐标为_________.
14.
将点P(-3,y)向下平移3个单位,再向右平移2个单位后得到点Q(x,-1),则xy=_____.
15.如图,在Rt△ABC中,∠ACB=90 ,∠BAC=60 ,AB=6.Rt△AB′C′可以看做是由
Rt△ABC绕A点按逆时针方向旋转60 得到的,则线段B′C的长为_________.
16.以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换能得到图(2)的有_________.(填序号)
①只要向右平移1个单位;
②先以直线AB为对称轴进行翻折,再向右平移1个单位;
③先绕着点O旋转180°,再向右平移1个单位;
④绕着OB的中点旋转180°即可.
三、解答题(共56分)
17.(10分)如图11,正方形网格中四边形ABCD的四个顶点都在格点上,若把四边形ABCD向右平移3个单位,试画出四边形ABCD平移后的图形.
18.
(10分)如图,四边形ABCD,四边形EFGH都是边长为1的正方形.
(1)这个图案可以看做是哪个“基本图案”通过旋转得到的?
(2)旋转中心是什么?经过旋转,点A,B,C,D分别移到什么位置?
19.(12分)如图13,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)作出△ABC以点C为对称中心的图形△;
(2)平移△ABC,若点A对应点的坐标为(0,-4),画出平移后对应的△;
(3)若将△绕某一点旋转可以得到△,请直接写出旋转中心的坐标.
20.(12分)请你利用角、线段、平行线、三角形、正方形、圆、半圆等基本图案,借助平移、旋转或轴对称设计一个图案,并简述你的设计意图.
21.(12分)如图,已知P为正方形ABCD外的一点,PA=1,PB=2.将△ABP绕点B按顺时针方向旋转90°,使点P旋转至点P′,且AP′=3,求∠BP′C的度数.
参考答案
一、1.A
2.C
3.B
4.C
5.B
6.D
7.C
8.B
二、9.④
10.②
11.10
12.2
13.(6,-5)
14.-2
15.
16.
②③④
三、17.
图略.
18.
解:(1)可以看做是由正方形ABCD为“基础图案”按顺时针方向旋转45°得到正方形EFGH.
(2)旋转中心是AC与BD的交点.点A,点B,点C,点D分别移到了点E,点F,点G,点H.
19.
解:
(1)画出△如图1所示:
(2)画出△如图1所示:
(3)旋转中心的坐标为(,-1).
20.解:答案不唯一,如图2所示:
21.
解:连接PP′,由旋转的性质得P′B=PB=2,∠PBP′=90°.
所以PP′==2,∠BPP′=45°.
因为PA=1,AP′=3,所以PA2+PP′2=AP′2.
所以∠APP′=90°.
所以∠APB=∠APP′+∠BPP′=135°.
所以∠BP′C=∠APB=135°.
图5
A
C
B
A
B
CB
DCB
图2
